THEMA 2: versnelling

QUARK_6-Thema-02-versnelling
Blz. 1
THEMA 2: versnelling
Gemiddelde versnelling bij een eendimensionale beweging
Een wagentje rijdt vanuit stilstand een helling af. De
hellingshoek is  .
De grootte van de snelheid vx van het wagentje neemt toe
als functie van de tijd t.
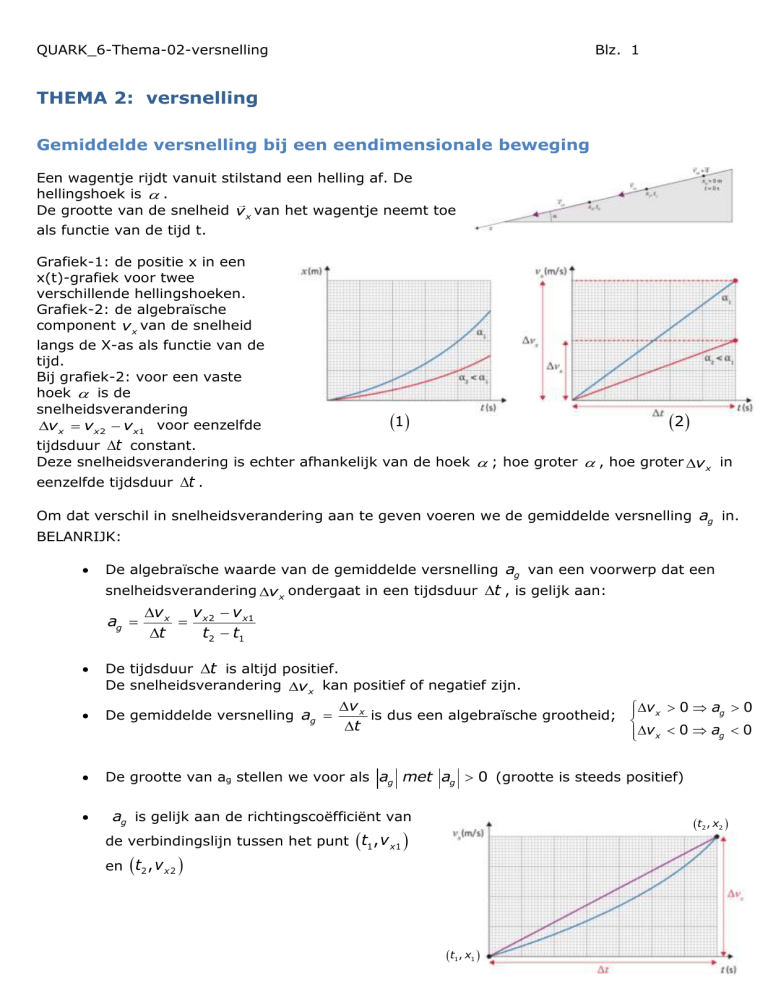
Grafiek-1: de positie x in een
x(t)-grafiek voor twee
verschillende hellingshoeken.
Grafiek-2: de algebraïsche
component vx van de snelheid
langs de X-as als functie van de
tijd.
Bij grafiek-2: voor een vaste
hoek  is de
snelheidsverandering
vx  vx2  vx1 voor eenzelfde
2 
1
tijdsduur t constant.
Deze snelheidsverandering is echter afhankelijk van de hoek  ; hoe groter  , hoe groter v x in
eenzelfde tijdsduur t .
Om dat verschil in snelheidsverandering aan te geven voeren we de gemiddelde versnelling ag in.
BELANRIJK:

De algebraïsche waarde van de gemiddelde versnelling ag van een voorwerp dat een
snelheidsverandering v x ondergaat in een tijdsduur t , is gelijk aan:
ag 
v x v x 2  v x1

t
t2  t1

De tijdsduur t is altijd positief.
De snelheidsverandering v x kan positief of negatief zijn.

De gemiddelde versnelling ag 

De grootte van ag stellen we voor als ag met ag  0 (grootte is steeds positief)

v x
v x  0  ag  0
is dus een algebraïsche grootheid; 

t
v x  0  ag  0
ag is gelijk aan de richtingscoëfficiënt van
t2 , x2 
de verbindingslijn tussen het punt  t1 , v x1 
en  t2 , v x 2 
t1, x1 
QUARK_6-Thema-02-versnelling
Blz. 2
Ogenblikkelijke versnelling bij een eendimensionale beweging
De ogenblikkelijke versnelling geeft informatie over de versnelling op 1 bepaald ogenblik t.
Op tijdstip t is ax de verhouding
dv x  t 
v x
v x

voor t  0 : ax  t   lim
t  0 t
dt
t
Je moet dus vx(t) afleiden naar t.
ax is gelijk aan de richtingscoëfficiënt van de raaklijn aan de vx (t)-grafiek op tet tijdstip t en geeft
aan hoe op dat tijdstip de snelheid van een voorwerp verandert per eenheid van tijd.
Op een as stellen we de versnelling ax voor door een pijl met het aangrijpingspunt op de plaats
van het voorwerp op het beschouwde tijdstip.
De index x bij ax geeft aan dat de versnellingsvector de richting heeft van de X-as.
De richting van de versnellingsvector ax is die van de baan.
Als op een tijdstip vx en ax dezelfde zin hebben, dan neemt de grootte van de snelheid van het
voorwerp toe; HET VERSNELT!!! vx en ax hebben hetzelfde teken
Als op een tijdstip vx en ax tegengesteld zijn, dan neemt de grootte van de snelheid van het
voorwerp af; HET VERTRAAGT!!! vx en ax hebben tegengesteld teken
Grootheid
Symbool
Eenheid
symbool
Versnelling
a
1 meter per seconde kwadraat
1 m/s²
Intermezzo: getallenvoorbeeld
QUARK_6-Thema-02-versnelling
Blz. 3
Eenparig veranderlijke beweging
Als de versnellingsfunctie a  t  van een voorwerp dat een eendimensionale beweging uitvoert
constant is maar verschillend van 0, dan voert het voorwerp een eenparige versnelde
rechtlijnige beweging of EVRB uit.
De v x  t  grafiek is een rechte, dus ax is constant en gelijk aan: ax 
Hieruit volgt: v x  ax .t  v x 2  v x1  ax .  t2  t1 
dv x
v x

dt
t
De snelheid v wordt dus op elk tijdstip t gegeven door de snelheidsfunctie:
v x  t   ax .t  v x 0
1
De positie x van het voorwerp wordt op elk tijdstip t gegeven door de plaatsfunctie:
x t  
ax .t 2
 v x 0.t  x0
2
2 
vx 0: beginsnelheid , x0: beginpositie
(uiteraard de snelheid en de positie van het voorwerp op het tijdstip t = 0 s)
De v x  t  grafiek is een rechte, de x  t  -grafiek is een parabool.
De resulterende kracht op het voorwerp is constant.
Voorbeeld: wagen en helling-op/helling-af
Let op de link tussen versnelling en snelheidswijziging!
Hoe zou je de situatie beschrijven als de wagen de
helling oprijdt en langs dezelfde kant terug afrijdt???
De valbeweging
De aarde oefent op elk voorwerp in haar omgeving een kracht uit. Dicht bij de aarde is de
zwaartekracht op dat voorwerp constant. Als het niet ondersteund wordt, zal het voorwerp onder
invloed van deze kracht een EVRB uitvoeren met een constante versnelling volgens de verticale
richting van de zwaartekracht. De versnelling van alle vallende voorwerpen in de omgeving van
het aardoppervlak is dezelfde; we noemen ze de valversnelling! In onze streken is de grootte van
de valversnelling
g  9, 81
m
.
s2
In (1) en (2) krijgen we dus ax  g  9, 81
m
s2
QUARK_6-Thema-02-versnelling
Blz. 4
Eenparig rechtlijnige beweging
De snelheid van een voorwerp dat op een rechte baan beweegt, en waar geen resulterende
kracht op werkt, blijft constant. Is het voorwerp in beweging, dan blijft zijn snelheid vx
constant en is ax  0
m
en vx  vx 0 .
s2
Het voorwerp voert een eenparige rechtlijnige beweging of ERB uit.
De snelheid v wordt dus op elk tijdstip t gegeven door de snelheidsfunctie v x  t   v x 0
De plaats-functie volgt uit: v x 
dx
x

en dus : x  t   v x 0.t  x0
dt
t
1
2 
De v x  t  grafiek is een horizontale rechte, de x  t  -grafiek is een schuine rechte.
De resulterende kracht op het voorwerp is nul!!
In het formularium met de verschillende interessegebieden (zoals ik ze op smartschool gedropt
heb), staan o.a. formuletjes van kinematica:
x
t
v X  v x 0  ax (t  t0 )
v gem 
x  x 0  v x 0 .(t  t0 ) 
v1x  v 2x
2
2
v v 2
x  x 2 x 1
2.ax
ax (t  t0 )2
2
v x , gem 
Het laatste formuletje is een bijzonder handig omdat het snelheid en plaats (+versnelling) linkt,
zonder dat je het tijdsinterval nodig hebt. Zeker proberen onthouden is de boodschap.
x 
v2e  vb2
2ax
Het is af te leiden door eliminatie van de tijd uit deze 2 meer bekende formules:
vX  vx 0  ax t  t0   t  t0  
x  x0  vx 0 . t  t0  
ax t  t0 
2
2
vx  vx 0
ax
1 
 v  vx 0
ax  x
 v  vx 0 
1 
 ax

 : x  x0  v x 0 .  x
2 
 
2
 ax 
 v  vx 0  ax vx  vx 0 
 2vx  2vx 0  vx  vx 0 
 x  x0  vx 0 .  x

x

x

v
.
 
 
0
x0 
2

2ax
2ax
2  ax 
 ax 


2
2
 2ax x  vx 0 . 2vx  2v x 0   vx  vx 0   2ax x  2vxvx 0  2vx20  vx2  2vxvx 0  vx20
2
 2ax x  2vx20  vx2  vx20  2ax x  vx2  vx20
2



QUARK_6-Thema-02-versnelling
Blz. 5
Ogenblikkelijke snelheid bij een tweedimensionale beweging
F
v
res
Ook bij tweedimensionale beweging; Beginsnelheid: v1  0 
 v2  v1  v
In een tijdsinterval met een tijdsduur wijzigt de snelheid v  v2  v1 .
In de limiet voor t  0 is de richting van a 
v
gelijk aan die van de richting van v !!!!
t
Bij een tweedimensionale beweging is de versnellingsvector a  t  op het tijdstip t:
a  t   lim
v  t 

dv  t 
t
dt
De versnellingsvector bestaat uit algebraïsche componenten die je
kan vinden door respectievelijke componenten van de
snelheidsvector af te leiden!
t  0
Op elk ogenblik versnellingsvector a  t  naar de binnenkant van

v x  t  dv x  t 

ax  t   lim
t 0

t
dt

v y  t  dv y  t 


ay  t   lim
t 0
t
dt
de baan en is de zin volgens de vector v  v2  v1 voor 2 tijdstippen rond het tijdstip t.
QUARK_6-Thema-02-versnelling
Blz. 6
Eenparige cirkelvormige beweging
Een punt van een langspeelplaat, een bord van een acrobaat, een tol of een windmolen voert een
eenparige cirkelvormige beweging of ECB uit.
De baan van zo'n punt is een cirkel met straal R, het punt beschrijft telkens een volledige cirkel in
dezelfde tijdsduur. We noemen deze tijdsduur, de periode T. Dat is dus m.a.w. de tijd nodig voor
één omwenteling.
De frequentie is het aantal omwentelingen per
seconde.
Hieruit volgt: f 
1
T
Het legt dus per omwenteling een afstand 2 R af gelijk aan de omtrek van de cirkel. De hoek
waarover elk punt van het voorwerp draait in een omwenteling is gelijk aan 2 .
Hoeksnelheid
In een tijdsinterval t is  de overeenkomstige hoekverplaatsing van elk punt van het
voorwerp.
De grootte van de hoeksnelheid  (“OMEGA”, niet ‘wee’) van een voorwerp dal een ECB uitvoert,
is de verhouding van hoekverplaatsing van een punt van het voorwerp tot het tijdsinterval dat
daarvoor nodig is:  

t
Neem je als hoekverplaatsing 2 , dan is hiervoor een tijd T nodig, en dus krijg je:

 2

 2 f
t
T
Grootheid
Symbool
Eenheid
symbool
Hoeksnelheid

1 radiaal per seconde
1 rad/s
Frequentie
f
1 omwenteling per seconde
1 s-1 = 1 Hz
Periode
T
Seconde
S1
QUARK_6-Thema-02-versnelling
Blz. 7
Baansnelheid
De baansnelheid is de snelheidsvector die raakt aan de baan en die
weergeeft hoeveel afstand het voorwerp per tijdseenheid aflegt.
Verband met  :
Veronderstel bij de start op t = 0 s, dat de beginhoek 0 rad is:

   0 


t
t  t0
t
Voor de algebraïsche componenten van de plaatsvector geldt dan:
 x t   R.cos    R.cos .t 

y t   R.sin    R.sin .t 
De algebraïsche componenten van de snelheidsvector worden hierdoor:
dx

v x  t   dt   R.sin .t 

v  t   dy   R.cos .t 
 y
dt
 v 
 v  t    v  t  
2
2
x
y
 R
Hoewel de grootte v van de snelheid van een punt van een
voorwerp dat een ECB beschrijft niet verandert, is er toch een
versnelling. Deze versnelling geeft de richtingsverandering weer van
de snelheid.
Uit de onderstaande figuren, waarbij de hoek  en dus ook
het tijdsinterval t steeds kleiner genomen worden, kun je
afleiden dat voor elk punt van de cirkel v en dus ook de
versnelling a voor t  0 gericht is naar het middelpunt van
de cirkel. (***)
De versnelling bij een ECB noemen we de
middelpuntzoekende of centripetale versnelling.
De algebraïsche componenten van de versnelling worden hierdoor:
dv x

2
ax  t   dt   R.cos .t 

a  t   dv y   2R.sin .t 
 y
dt
 a 

 ax t    ay t 
2

2
v  R
  2R 
a 
v2
R
(***) Je kan dat ook wiskundig bewijzen door a.v uit te rekenen!!
Zie ook naar de begrippenkaart!
QUARK_6-Thema-02-versnelling
Blz. 8
Probeer zelf eens te bewijzen dat
1. de positie en de versnelling dezelfde richting maar tegengestelde zin hebben.
2. de snelheid en de versnelling loodrecht op elkaar staan!
Hint: voor (2) maak je gebruik van het ‘scalair product’ van vectoren!
…
Voorbeeldopdracht-1
Een skiër daalt vanuit rust op t = 0 s een
berghelling af met een constante versnelling van
4,0 m/s2. De helling is 25 m lang. Verwaarloos
eventuele wrijving.
 Bereken de positie en de snelheid na 3,0 s.
 Bereken het tijdstip wanneer hij beneden
aankomt en zijn snelheid daar.

Maak de x(t)- en v(t)-grafiek (zie boek!)
Oplossing: de skiër voert een EVRB uit, dus:
x t  
ax .t 2
 v x 0.t  x0
2
2 
x  0   0 m  x0  0 m en v x  0   0
m
m
 v x 0  0 m en gegeven : ax  4, 0 2
s
s
m 2
.t
2
2
m
m
s
Dus 2  wordt : x  t  
 2, 0 2 .t 2 en daaruit x 3, 0 s   2, 0 2 . 3, 0 s   18 m
2
s
s
m
m
m
Voor de snelheid : v x t   ax .t  v x 0  4, 0 2 .t en daaruit v x 3, 0 s   4, 0 2 . 3, 0 s   12
s
s
s
Op welk tijdstip is de positie 25 m ?
4, 0
x t 
en dus voor xe  25 m : te 
m
2, 0 2
s
m
m
Dan is v : v x 3,5 s   4, 0 2 . 3,5 s   14
s
s
( zie boek voor grafieken)
Uit x  t   2, 0
m 2
.t vo lg t t 
s2
25 m
 3,5 s
m
2, 0 2
s
QUARK_6-Thema-02-versnelling
Blz. 9
Voorbeeldopdracht-2
Een auto rijdt met een snelheid van 28 m/s op een horizontale weg en remt met een constante
versnelling van 4,0 m/s².
 Maak een situatieschets. Teken de snelheid en de versnelling van de auto juist nadat
hij begint te remmen, en juist voor hij stopt. Teken de krachten en de resulterende
kracht op de auto. Welke beweging voert de auto uit?
 Na hoeveel tijd komt hij tot stilstand?
 Wat is dan de positie van de auto?
 Maak de x(t)- en v (t)-grafiek.
Oplossing: We kiezen de zin van de as
volgens de beweging. Op het tijdstip t = O
s begint de auto te remmen. De auto remt,
dus zijn snelheid en versnelling
tegengesteld. Als de auto remt, werken er
drie krachten op: de zwaartekracht, de
normaalkracht en de wrijvingskracht:
Voor het bepalen van de versnelling : v x  t   ax .t  v x 0  t 
v x t   v x 0
Op het einde is de snelheid nul , dus voor t  t e (t ' einde ') : t e 
ax
v x  te   v x 0
ax
m
s  7, 0 s

m
4, 0 2
s
0  28
ax .t 2
 v x 0.t  x0
2
2
m

 4, 0 s2  . 7, 0 s 
m


Op t  te  7, 0 s; invullen: x 7, 0   
  28
. 7, 0 s   0 m  98 m
2
s 

Voor de positie geldt : x  t  
Voorbeeldopdracht-3
Een zeiler komt in moeilijkheden, hij ligt stil en schiet een vuurpijl recht omhoog af. De pijl schiet
weg met een snelheid van 100 km/h. Verwaarloos de luchtweerstand.
a) Maak een situatieschets. Welke beweging voert de pijl uit?
b) Bereken het tijdstip tm waarop de pijl op zijn hoogste punt is. Bereken de maximale hoogte
xm van de pijl.
c) Bereken de snelheid en de plaats van de pijl na 1,00 s.
d) Bereken de snelheid vxv waarmee de pijl weer voorbij het vertrekpunt komt.
e) Schets de snelheid en de versnelling op een x-as. Maak je tekening op schaal.
Oplossing:
a) De pijl voert een EVRB uit!!
Je kunt de richting en de zin van de as altijd vrij kiezen. We nemen een
verticale, naar omhoog gerichte as, en leggen de oorsprong in het punt waar
de pijl start op t = 0 s. Door de keuze van de as is de algebraïsche waarde van
de beginsnelheid positief en die van de valversnelling negatief.
Tijdens het stijgen vertraagt de pijl; vx en ax zijn tegengesteld.
Tijdens het dalen versnelt de pijl; vx en ax hebben dezelfde zin.
(Let dus goed op! De versnelling blijft de hele tijd naar beneden wijzen!
We zien in het volgende hoofdstuk dat dit rechtstreeks te maken heeft met de
zwaartekracht en die blijft uiteraard ook de hele tijd naar beneden wijzen!)
QUARK_6-Thema-02-versnelling
Blz. 10
b) Maximale hoogte
km
m
m
 27, 8
en vast gegeven : ax  g  9, 81 2
h
s
s
m
ax wijst de hele tijd naar beneden, dus : ax  9, 81 2 .
s
Let dus goed op !! Er is voor de hele beweging ( EN ) slechts 1 enkele plaatsfunctie en
x  0   0 m  x0  0 m en v x  0   100
slechts 1 enkele ax  9, 81
m
!!!!
s2
Dus : Voor de snelheid : v x t   ax .t  v x 0  9, 81
In het hoogste punt is v xm
m
m
.t  27, 8
2
s
s
m
0
. Invullen in 1 geeft : t m 
s
1
m
s  2, 83 s
m
9, 81 2
s
27, 8
Deze tijd gaan we nu in de plaatsfunctie invullen :
Eerst de waarden invullen voor ax e.d. : x t  
m 2
.t
m
s2
 27, 8
.t  0 m
2
s
9, 81
2
m
. 2, 83 s 
2 
m
s
Dus 2  wordt : x  tm  
 27, 8
. 2, 83 s   39,3 m
2
s
c) snelheid en plaats na 1,00 s
m
m
m
Dus : Voor de snelheid : v x 1, 0 s   9, 81 2 .1, 0 s  27, 8
 18, 0
s
s
s
2
m
9, 81 2 . 1, 0 s 
m
s
Voor de plaats : x 1, 0 s  
 27, 8
. 1, 0 s   22, 9 m
2
s
d) snelheid waarmee pijl aan vertrekpunt voorbijkomt:
We zoeken het tijdstip ' tv ' via de plaatsfunctie :
9, 81
we leggen op aan 2  dat de plaats 0 m moet zijn :
2
m
. t
2  v
m
s
 x  tv  
 27, 8
.  tv   0 m
2
s
m

 9, 81 s2 .tv
m
We lossen tv hier uit op : 
 27, 8
2
s


m

2.  27, 8
s 
 tv  0  tv  
 5, 66 s
m
9, 81 2
s
De snelheid is dan :
m
m
m
v x  t   9, 81 2 .5, 66 s  27, 8
 27, 8 !
s
s
s
 kan je de nodige uitleg hierbij verzinnen ?
e) zie boek voor grafieken.
9, 81


 .tv  0


2 
QUARK_6-Thema-02-versnelling
Blz. 11
Voorbeeldopdracht-4
De positie van een elektrische wagentje wordt gegeven door
volgende algebraïsche componenten van de plaatsvector:
Bereken de grootte van de versnelling op t = 1,2 s.
Oplossing:
We leiden de RESPECTIEVE PLAATSFUNCTIES af!!!
vx t
vy t
dx t
d 1,5 m
0,30
dt
dy t
m 2
.t
s2
0, 60
dt
m
.t
s
d 1, 0
dt
1, 0
dt
x t
1,5 m
y t
1,0
0,30
m 2 de
.t
s2
m
.t
s
m
.t
s2
m
s
En nu leiden we de RESPECTIEVE SNELHEIDSFUNCTIES af en vullen de waarde voor de variabele
t in met 1,2 s:
ax t
d
dv x t
0, 60
m
.t
s2
0, 60
ax 1,2 s
dt
m
d 1, 0
dv y t
m
s
ay t
0 2
ay 1,2 s
dt
dt
s
Ter info: de grootte van de versnelling is:
a
dt
m
s2
ax t
2
ay t
2
0,60
m
s2
2
0
m
s2
0
0, 60
m
s2
m
s2
2
0,60
m
s2
In het boek wordt de versnellingsvector getekend; zie boek…
Voorbeeldopdracht-5
Jorge slingert een emmer in een horizontaal vlak rond met een constante baansnelheid.
De straal van de cirkel is 1,2 m, de emmer draait in 5,0 s driemaal rond. a Bereken de
periode en de frequence, b Welke afstand heeft de emmer afgelegd in 1,5 s? c Bereken
de grootte van de hoeksnelheid, de baansnelheid en de centripetale versnelling.
Oplossing:
a) periode is de tijd voor 1 rondgang. De emmer draait 3 keer rond in 5,0 s; dus de tijd voor
5, 0 s
1,7 s
3
1
1
0, 60 s
De frequentie is f
T
1,7 s
1 rondgang is T
1
0, 60 Hz
b) via redenering: zie boek
2 f
c)
v
2 f
.R
2 .0, 60
3, 8
rad
s
rad
.1,2 m
s
rad
s
m
4,5
s
3, 8
2
a
2
.R
3, 8
rad
.1,2 m
s
17
m
s2
of a
v2
R
m
4,5
s
1,2 m
2
17
m
s2