Hoofdstuk 1 - Functies

er
sb
v
Hoofdstuk 1 - Functies
Hoofdstuk 1 - Functies
Voorkennis
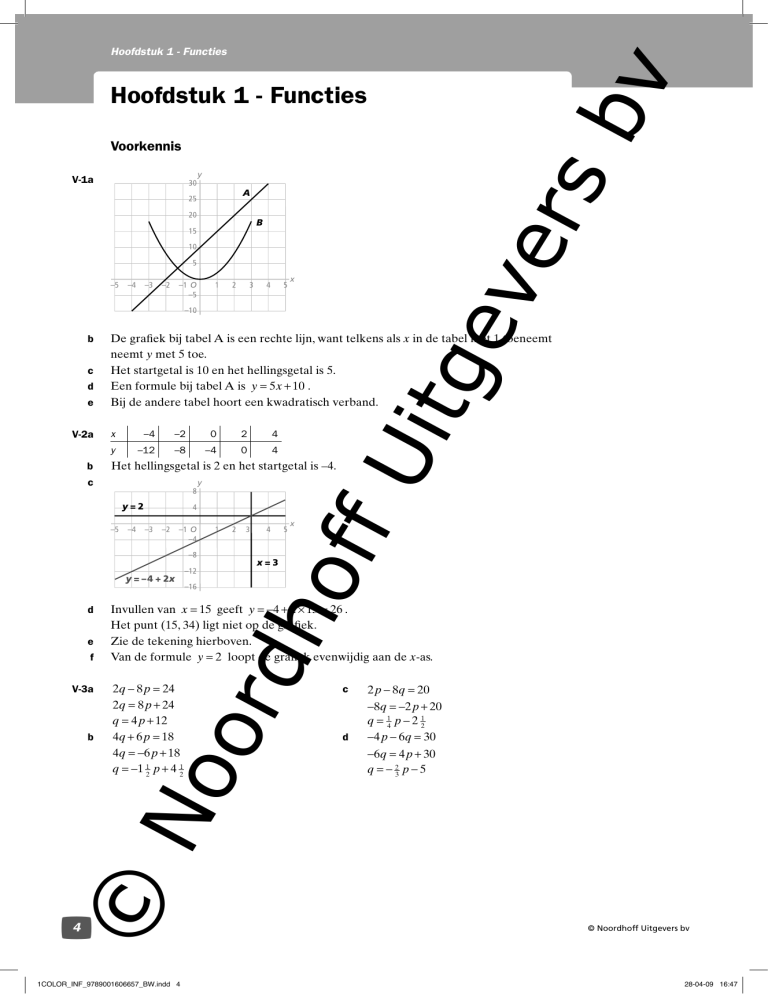
V-1a
30
y
A
25
20
B
15
10
5
–4
–3
–2
–1 O
–5
1
2
3
4
5
x
ev
–5
–10
c
d
e
V-2a
b
De grafiek bij tabel A is een rechte lijn, want telkens als x in de tabel met 1 toeneemt
neemt y met 5 toe.
Het startgetal is 10 en het hellingsgetal is 5.
Een formule bij tabel A is y = 5 x + 10 .
Bij de andere tabel hoort een kwadratisch verband.
x
–4
–2
0
2
4
y
–12
–8
–4
0
4
Het hellingsgetal is 2 en het startgetal is –4.
c
8
y=2
–5
–4
y
4
–3
–2
–1 O
–4
1
2
–8
y = – 4 + 2x
f
x
–16
Invullen van x = 15 geeft y = −4 + 2 × 15 = 26 .
Het punt (15, 34) ligt niet op de grafiek.
Zie de tekening hierboven.
Van de formule y = 2 loopt de grafiek evenwijdig aan de x-as.
2q − 8 p = 24
2q = 8 p + 24
q = 4 p + 12
4q + 6 p = 18
4q = −6 p + 18
q = −1 12 p + 4 12
©
V-3a
b
5
dh
e
4
or
d
3
x=3
–12
No
Ui
tg
b
off
⁄
4
1COLOR_INF_9789001606657_BW.indd 4
c
d
2 p − 8q = 20
−8q = −2 p + 20
q = 14 p − 2 12
−4 p − 6q = 30
−6q = 4 p + 30
q = − 23 p − 5
© Noordhoff Uitgevers bv
28-04-09 16:47
V-4a
x
–4
–3
6
2 12
y
–2
–1
0
0 −1 12
7
1
–2 −1 12
2
3
4
0
2 12
6
er
sb
v
Hoofdstuk 1 - Functies
y
6
1
y = 2 x2 – 2
5
4
3
ev
2
1
–5
–4
–3
–1 O
–1
–2
1
2
3
4
x
5
–2
b
V-5a
b
Zo’n grafiek noem je een dalparabool.
Ui
tg
–3
Van parabool 1 is (0, 0) de top en het is een dalparabool.
Van parabool 2 is (0, –2) de top en het is een dalparabool.
Van parabool 3 is (0, 2) de top en het is een bergparabool.
Van parabool 4 is (0, –1) de top en het is een bergparabool.
Bij parabool 1 hoort formule A, bij parabool 2 hoort formule B, bij parabool 3 hoort
formule D en bij parabool 4 hoort formule C.
De wortel uit een negatief getal bestaat niet.
R
0
1
2
3
4
5
6
7
8
9
v
0
3
4,24
5,20
6
6,71
7,35
7,94
8,49
9
c
10
off
V-6a
b
v
dh
9
8
v=3 R
7
6
5
3
2
1
d
0
1
2
3
4
5
6
7
8
9
10
R
No
0
or
4
15 = 3 R
R =5
©
R = 25
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 5
⁄
5
28-04-09 16:47
er
sb
v
Hoofdstuk 1 - Functies
V-7a
x
–4
–3
–2
–1
0
1
2
3
4
5
6
y
-
0
1
1,41
1,73
2
2,24
2,45
2,65
2,83
3
b
4
y
y= x+3
3
2
1
e
d
–2
–1 O
–1
1
2
3
4
5
6
x
De coördinaten van het randpunt zijn (–3, 0).
Invullen van x = 46 geeft y = 46 + 3 = 49 = 7 .
Ja, het punt (46, 7) ligt op de grafiek.
Invullen van x = 141 geeft y = 141 + 3 = 144 = 12 .
Nee, het punt (141, 11) ligt niet op de grafiek.
Ui
tg
c
–3
1-1 Functies
1a
b
d
25
T in °C
c
Op de grond is het 20 − 0, 006 × 0 = 20 C.
Op 8000 meter hoogte is de temperatuur 20 − 0, 006 × 8000 = −28 C.
20 − 0, 006 × h = 0
0, 006 × h = 20
h ≈ 3333 meter
20
15
10
T = 20 – 0,006h
5
–5
2000
–10
–15
–20
–25
2a
b
d
20 − 0, 006 × h = −40
0, 006 × h = 60
h = 10 000
Deze vliegtuigen kunnen op een maximale hoogte van 10 000 meter vliegen.
Sven heeft de temperatuur voor een hoogte van 1500 meter berekend.
T(1200) = 20 − 0, 006 × 1200 = 12, 8
De temperatuur op 1100 meter hoogte is T(1100) = 20 − 0, 006 × 1100 = 13, 4 C.
De temperatuur op 4550 meter hoogte is T(4550) = 20 − 0, 006 × 4550 = −7, 3 C.
20 − 0, 006 × h = −10
0, 006 × h = 30
h = 5000
De temperatuur is –10 C op een hoogte van 5000 meter.
©
c
⁄
6
8000
10 000
h in m
No
e
6000
or
–30
4000
dh
0
off
ev
–4
1COLOR_INF_9789001606657_BW.indd 6
© Noordhoff Uitgevers bv
28-04-09 16:47
4a
b
c
d
5a
b
c
d
e
6a
b
d
L(3) = 3 × 3 + 16 = 25 en L(10) = 3 × 10 + 16 = 46
Als aan de veer een massa van 3 kg hangt, dan heeft de veer een lengte van 25 cm.
Als aan de veer een massa van 10 kg hangt, dan heeft de veer een lengte van 46 cm.
L( m) = 3m + 16
31 = 3m + 16
3m = 15
m=5
Bij een massa van 5 kg heeft de veer een lengte van 31 cm.
3m + 16 = 17, 5
3m = 1, 5
m = 0, 5
Bij een massa van 0,5 kg heeft de veer een lengte van 17,5 cm.
f (4) = 12 × 4 − 3 = −1 en g(−1) = −(−1)2 + 1 = 0
1
x−3=2
2
1
x=5
2
x = 10
1
x − 3 = 44
2
1
x = 47
2
x = 94
− x 2 + 1 = −3
− x 2 = −4
x2 = 4
x = 2 of x = −2
Voor alle punten op de horizontale lijn geldt y = 1 dus voor iedere x geldt h( x) = 1 .
f (0) = 3 , g(4) = −1 en h(−1) = 1
h(−5) bestaat niet.
Voor de functie f geldt f (0) = 3 en niet f (0) = 4 .
Het goede functievoorschrift is f ( x) = − 12 x 2 + 3 .
Bij de functie h gebruikt Marieke een minteken in plaats van een plusteken.
Het goede functievoorschrift is h( x) = x + 2 .
g ( x) = −1
©
c
ev
d
Ui
tg
c
off
b
dh
Invullen van a = 10 geeft 2 × 10 + 6b = 10 oftewel 20 + 6b = 10 , dus 6b = −10 en
b = −1 23 .
Invullen van b = 3 geeft 2 a + 6 × 3 = 10 oftewel 2 a + 18 = 10 , dus 2 a = −8 en a = −4 .
2 a + 6b = 10
2 a = −6b + 10
a = −3b + 5 oftewel a = 5 − 3b
2 a + 6b = 10
6b = −2 a + 10
b = − 13 a + 1 23
or
3a
No
er
sb
v
Hoofdstuk 1 - Functies
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 7
⁄
7
28-04-09 16:47
7a/b
10
er
sb
v
Hoofdstuk 1 - Functies
y
a=1
8
6
4
2
–5
–4
–3
–2
a = –3
–1 O
–2
1
2
3
4
5
x
–4
ev
–6
–8
–10
c
d
Invullen van x = 0 en y = 0 geeft 0 = 2 × 0 + a , dus a = 0 .
Invullen van x = 4 en y = 26 geeft 26 = 2 × 4 + a oftewel 26 = 8 + a , dus a = 18 .
Ui
tg
1-2 Domein en bereik
8a
b
9a
c
d
Als je x = 0 invult, dan krijg je f (0) = 0 − 5 = −5 , maar de wortel uit een negatief
getal bestaat niet.
Het kleinste getal dat je kunt invullen is x = 5 .
De kleinste uitkomst die je kunt krijgen is f (5) = 5 − 5 = 0 = 0 .
Het kleinste getal dat je kunt invullen is x = 5 .
De kleinste uitkomst die je kunt krijgen is g(5) = 2 + 5 − 5 = 2 + 0 = 2 .
Invullen van x = 0 geeft g(0) = 3 + 2 0 − 2 = 3 + 2 −2 , maar de wortel uit een
negatief getal bestaat niet.
x
0
y
b
9
1
2
kan niet kan niet
3
y
8
7
6
3
2
1
3
5
6
7
5
5,83
6,46
7
7,47
4
5
6
7
8
9
10
x
De coördinaten van het randpunt van de grafiek zijn (2, 3).
Het domein van g is x ≥ 2 en het bereik van g is y ≥ 3 .
©
d
2
No
c
1
or
4
4
g (x) = 3 + 2 x –2
5
O
3
dh
off
⁄
8
1COLOR_INF_9789001606657_BW.indd 8
© Noordhoff Uitgevers bv
28-04-09 16:47
10a
b
er
sb
v
Hoofdstuk 1 - Functies
Alle waarden van x vormen het domein van h.
x
–3
–2
–1
0
1
2
3
y
–8
–3
0
1
0
–3
–8
c
4
y
2
–5
–4
–3
–2
h (x) = 1 – x2
–1 O
–2
1
2
3
4
5
x
ev
–4
–6
–8
–10
b
12a
b
c
13a
b
14a
b
c
d
e
c
–3
–2
–1
y
kan niet
0
2,24
2,83
0
1
2
3
2,83
2,24
3
4
0 kan niet
Ja, de tabel klopt met de grafiek.
Het domein van f is −3 ≤ x ≤ 3 en het bereik van f is 0 ≤ y ≤ 3 .
f ( 7) = 3 − 2 × 7 = −11
3 − 2x = 7
2 x = −4
x = −2
Nee, je mag alle getallen in deze functie invullen.
Nee, je kunt alle getallen als uitkomst krijgen.
g( 7) = 9 − 2 × 72 = −89
9 − 2 x2 = 7
2 x2 = 2
x2 = 1
x = 1 of x = −1
Nee, je mag alle getallen in deze functie invullen.
Ja, je kunt geen getallen groter dan 9 als uitkomst krijgen.
Getallenlijn 1 hoort bij ongelijkheid C, getallenlijn 2 hoort bij ongelijkheid F en
getallenlijn 3 hoort bij ongelijkheid B.
Interval 1 hoort bij de ongelijkheid x ≤ −1 en bij de intervalnotatie ⟨←, −1 ] .
Interval 2 hoort bij de ongelijkheid −2 ≤ x < 4 en bij de intervalnotatie [−2, 4 ⟩ .
Interval 3 hoort bij de ongelijkheid x > 1 en bij de intervalnotatie ⟨1, →⟩ .
Het domein van f is x ≥ 0 .
Het bereik van f is y ≥ −2 .
Het bereik van g zijn alle getallen.
Kenneth bedoelt dat alle getallen het domein van g vormen.
©
d
–4
Ui
tg
x
off
11a
De coördinaten van de top van de grafiek zijn (0, 1).
Het bereik van h is y ≤ 1 .
dh
e
or
d
No
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 9
⁄
9
28-04-09 16:47
er
sb
v
Hoofdstuk 1 - Functies
1-3 Functies en parameters
15a
b
c
Het functievoorschrift is f ( x) = 2 x + 3 .
Bij deze lijn hoort de lineaire functie g ( x) = 12 x + 3 .
Alle functievoorschriften zijn van de vorm h( x) = ax + 3 waarbij a een getalletje is.
6
16a/b
y
5
ev
4
3
2
1
–4
–3
–2
–1 O
–1
b=3
1
2
3
4
5
x
Ui
tg
–5
–2
–3
b=2
–4
b = –1
–5
17a
b
Invullen van x = 3 en y = 7 geeft 7 = −3 + b , dus b = 10 .
Bij een hoogte van 10 cm hoort de formule I = 10 x 2 .
400
350
300
250
off
c
l in cm3
I = 10x 2
200
I = 5x 2
150
100
0
c
d
1
2
3
4
5
6
7
8
9
x in cm
10
Bij een hoogte van 5 cm hoort de formule I = 5 x 2 . Zie de tekening hierboven.
Bij een hoogte van 2 cm hoort de formule I = 2 x 2 . De bijbehorende grafiek is een
parabool die nog minder snel stijgt dan de vorige grafieken.
©
No
or
0
dh
50
⁄
10
1COLOR_INF_9789001606657_BW.indd 10
© Noordhoff Uitgevers bv
28-04-09 16:47
18a
er
sb
v
Hoofdstuk 1 - Functies
De massa van een houten kubus met een ribbe van 8 cm is 0, 8 × 8 3 = 409, 6 gram.
b/c
m in grammen
300
280
260
240
220
200
180
m = 2,6 r 3
ev
160
140
120
100
40
m = 0,8 r 3
20
0
d
1
3
2
4
r in cm
Invullen van r = 5 en m = 30 geeft 30 = d × 53 oftewel 30 = 125d , dus d = 0, 24 .
De dichtheid van kurk is 0,24.
19a/b
30
y
a=2
25
20
15
10
a=1
5
–4
–3
–2
–1 O
–5
–10
–15
–20
–25
c
20a
2
3
4
5
x
a = –1
or
–30
1
dh
–5
5
off
0
Ui
tg
80
60
Invullen van x = 2 en y = −6 geeft −6 = a(2 2 − 1) oftewel −6 = 3a , dus a = −2 .
6
y
No
5
4
f (x) = 2 + x – 1
3
2
1
O
b
c
2
3
d
4
5
6
7
8
9
10
x
Het domein van f is [1, →⟩ .
Het bereik van de functie f is [ 2, →⟩ .
Het domein is dan [−5, →⟩ . Het bereik is dan [−10, →⟩ .
©
1
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 11
⁄
11
28-04-09 16:47
21a
b
c
d
De coördinaten van de top van de grafiek van f zijn (0, 1).
De vergelijking x 2 + 1 = 5 heeft twee oplossingen, want de lijn y = 5 snijdt de grafiek
van f in twee punten.
Voor p = 1 heeft de lijn y = p precies één gemeenschappelijk punt met de grafiek
van f, want de lijn y = 1 gaat door de top van de parabool.
Voor p > 1 snijdt de lijn y = p de grafiek van f in twee punten.
1-4 Recht evenredig en omgekeerd evenredig
22a
V in cm3
10
15
20
30
m in gram
78
117
156
234
7,8
7,8
7,8
7,8
m
in gram/cm3
V
Ui
tg
ev
er
sb
v
Hoofdstuk 1 - Functies
In de derde rij komt telkens hetzelfde getal te staan.
Als V twee keer zo groot wordt, dan wordt m ook twee keer zo groot.
23a
b
c
Ja, tussen de prijs en het gewicht van een stuk kaas is sprake van een recht evenredig
verband.
Nee, de kosten van een mobieltje per maand hangen niet alleen maar af van het
aantal minuten dat je belt.
Nee, als de wandeling bijvoorbeeld honderd keer zo lang wordt, dan wordt de tijd die
je erover doet meer dan honderd keer zo lang omdat je tempo dan lager wordt.
24a
b
25a
b
26a
b
Lia doet er 30 : 15 = 2 uur over.
Ze moet dan met een snelheid van 30 km per uur rijden.
c
snelheid in km per uur
5
10
15
30
tijd in uren
6
3
2
1
dh
De hoogte is niet recht evenredig met de temperatuur, want 5, 3 : 35 ≈ 0, 151 ;
6, 1 : 45 ≈ 0, 136 ; 6, 9 : 55 ≈ 0, 125 en 7, 7 : 65 ≈ 0, 118 .
Telkens als de temperatuur met 10 C toeneemt, neemt de hoogte met 0,8 cm toe.
Er is dus sprake van een lineair verband met hellingsgetal 0, 8 : 10 = 0, 08 .
Het startgetal is 5, 3 − 35 × 0, 08 = 2, 5 .
Een formule die het verband aangeeft is h = 0, 08T + 2, 5 .
©
No
De variabelen x en y zijn recht evenredig. De evenredigheidsconstante is 2,4.
De variabelen x en y zijn niet recht evenredig.
De variabelen x en y zijn recht evenredig. De evenredigheidsconstante is 2,5.
or
c
off
b
⁄
12
1COLOR_INF_9789001606657_BW.indd 12
© Noordhoff Uitgevers bv
28-04-09 16:47
27a
b
c
De variabelen x en y zijn omgekeerd evenredig.
Een bijbehorende formule is x × y = 120 of y = 120 of x = 120 .
x
y
De variabelen x en y zijn niet omgekeerd evenredig.
Telkens als x met 5 toeneemt neemt y met 3 af, dus het hellingsgetal is −3 : 5 = −0, 6 .
Het startgetal is 12 + 3 = 15 . Een bijbehorende formule is y = 15 − 0, 6 x .
De variabelen x en y zijn omgekeerd evenredig.
b
c
d
Als de hoogte twee keer zo groot wordt, dan wordt de gemiddelde snelheid twee
keer zo klein.
Ja, de variabelen h en v zijn omgekeerd evenredig.
Een formule is h × v = 150 of v = 150 of h = 150 .
h
v
Deze formule is zinvol als v tussen ongeveer 5 km per uur en ongeveer 50 km per
uur zit.
1-5 Gebroken functies
29a
lengte l in cm
breedte b in cm
1
2
3
4
6
12
12
6
4
3
2
1
10
9
off
breedte b in cm
8
7
6
5
3
2
1
c
d
e
f
2
3
4
5
6
7
8
9
lengte l in cm
10
De lengte en de breedte van deze rechthoek zijn omgekeerd evenredig want
lengte keer breedte moet 12 zijn.
Omdat l ⋅ b = 12 , geldt b = 12 .
l
b(l ) = 12
l
b(100) = 0, 12 ; b(10) = 1, 2 ; b(1) = 12 ; b(0, 1) = 120 en b(0, 01) = 1200
No
1
Het domein van de functie b is ⟨0, →⟩ en het bereik van b is ⟨0, →⟩ .
©
b
0
or
0
dh
4
Ui
tg
28a
14, 4
14, 4
of x =
.
x
y
ev
Een bijbehorende formule is x × y = 14, 4 of y =
er
sb
v
Hoofdstuk 1 - Functies
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 13
⁄
13
28-04-09 16:47
30a
b
Voor x = 2 is de uitkomst f (2) = 4 = 2 .
2
4
Voor x = 12 is de uitkomst f ( 12 ) = 1 = 8 en voor x = − 12 is de uitkomst
2
f (− 12 ) = 41 = −8 .
−2
Invullen van x = 0 geeft f (0) = 4 , maar je kunt niet delen door 0.
0
c
d
x
–4
–2
–1
− 12
y
–1
–2
–4
–8
e
Als x twee keer zo groot wordt, dan wordt y twee keer zo klein.
Of:
Het product van x en y is telkens 4.
f
0
1
4
1
2
1
–16 kan niet
16
8
4
y
f (x) =
8
4
x
4
–5
–4
–3
–2
–1 O
–4
1
2
3
4
5
x
–8
–12
–16
31a
x
0
1
2
y
–2
–3
–6
2
4
2
1
ev
− 14
2,9
Ui
tg
16
12
er
sb
v
Hoofdstuk 1 - Functies
3
3,1
6
100
–60 kan niet
60
2
0,06
b
c
d
6 = 6 = −2 en dat bestaat gewoon.
0 − 3 −3
Invullen van x = 3 geeft f (3) = 6 = 6 en dat bestaat niet.
3−3 0
Als x steeds groter wordt, dan naderen de uitkomsten naar 0.
e
Als x steeds kleiner wordt, dan naderen de uitkomsten ook naar 0.
f
Eerst oplossen van
off
Invullen van x = 0 geeft f (0) =
32a/b
5
or
4
y
dh
6 = −1000 geeft x − 3 = −0, 006 , dus x = 2, 994 .
x−3
Bijvoorbeeld voor x = 2, 995 is de uitkomst kleiner dan –1000.
3
a = –2
a=2
2
1
–4
–3
–2
–1 O
–1
1
2
No
–5
a=2
–2
–3
3
4
5
x
a = –2
–4
–5
De x-as en de y-as zijn de asymptoten.
De grafiek bij een negatief getal is gespiegeld ten opzichte van de x-as of de y-as.
Invullen van x = 2 en y = 3 geeft 3 = a , dus a = 6 .
2
©
c
d
⁄
14
1COLOR_INF_9789001606657_BW.indd 14
© Noordhoff Uitgevers bv
28-04-09 16:47
33a
b
d
c
x
–2
y
–1
–1
−1
0
1
–2
1
3
2
3
4
5
–4 kan niet
4
2
1 13
De functie bestaat niet voor x = 2 .
Als x heel dicht bij 2 in de buurt komt, dan worden de uitkomsten heel erg groot of
heel erg klein.
Als x steeds groter wordt, dan naderen de uitkomsten naar 0.
e
5
y
4
ev
f (x) = x 4– 2
3
2
–3
–2
–1 O
–1
1
2
3
4
5
6
7
x
–2
–3
–4
–5
34a
b
c
d
Een formule voor de verticale asymptoot is x = 2 .
De waarde x = 2 hoort niet tot het domein.
De coördinaten van het snijpunt met de x-as zijn (4, 0) en de coördinaten van het
snijpunt met de y-as zijn (0, –2).
Een formule van de verticale asymptoot is x = 2 en een formule van de horizontale
asymptoot is y = −1 .
Bij deze grafiek hoort de waarde a = −2 .
e
4
off
f
Ui
tg
1
er
sb
v
Hoofdstuk 1 - Functies
y
dh
3
2
1
–6
–5
–4
–3
–2
–1 O
–1
1
2
3
4
x
or
–2
–3
f (x) = – 1 +
b
–4
–5
Invullen van t = 0 geeft T(0) = 4 + 60 = 24 . Op het moment dat het blikje in de
0+3
koelkast wordt gezet is de temperatuur van het blikje 24 C.
No
35a
5 = 4 + 60
t+3
60 = 1
t+3
t + 3 = 60
©
2
x+1
t = 57
Na 57 minuten is de temperatuur 5 C.
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 15
⁄
15
28-04-09 16:47
c
Op den duur wordt de temperatuur van de cola 4 C.
Dat betekent dat de grafiek van T een horizontale asymptoot heeft.
d
t
T
0
7
17
27
37
47
57
24
10
7
6
5,5
5,2
5
T in °C
24
22
20
18
ev
16
14
12
10
T (t) = 4 +
6
60
t+3
Ui
tg
8
4
2
0
e
0
10
20
30
40
50
60
70 80 90 100
t in minuten
De grafiek zou een verticale asymptoot kunnen hebben als de noemer gelijk is aan 0,
maar dan moet gelden t + 3 = 0 oftewel t = −3 en een negatieve tijd kan niet.
b
37a
b
c
Op een diepte van 200 meter is de temperatuur 20 + 0, 03 × 200 = 26 graden Celsius.
T (d) = 20 + 0, 03d
Voor die mijn geldt T (d) = b + 0, 03d met b de buitentemperatuur. Invullen van
d = 400 en T (d) = 30 geeft 30 = b + 0, 03 × 400 oftewel 30 = b + 12 , dus b = 18 .
Bij die mijn is de buitentemperatuur 18 graden Celsius.
dh
36a
off
1-6 Gemengde opdrachten
er
sb
v
Hoofdstuk 1 - Functies
De functie f is een wortelfunctie, g is een kwadratische functie, h is een constante
functie, k is een lineaire functie en l is een omgekeerd evenredige functie.
y
8
6
k (x) = 2x + 1
or
4
2
–3
–2
–1
O
–2
1
2
3
x
No
–4
–6
–8
–10
g (x) = –2x 2 + 5
–12
–14
–16
c
De coördinaten van dat punt zijn (1, 3).
©
⁄
16
1COLOR_INF_9789001606657_BW.indd 16
© Noordhoff Uitgevers bv
28-04-09 16:47
d
38a
er
sb
v
Hoofdstuk 1 - Functies
f (1) = 2 × 1 + 7 = 9 = 3 , g(1) = −2 × 12 + 5 = −2 + 5 = 3 , h(1) = 3 , k(1) = 2 × 1 + 1 = 3
en l(1) = 3 = 3 .
1
f (−7) = 25 − (−7)2 = 25 − 49 = −24 en dat bestaat niet,
f (−5) = 25 − (−5)2 = 25 − 25 = 0 , f (−3) = 25 − (−3)2 = 25 − 9 = 16 = 4 ,
f (−2) = 25 − (−2)2 = 25 − 4 = 21 ≈ 4, 48 , f (0) = 25 − 0 2 = 25 − 0 = 5 ,
b
c
f (5) = 25 − 52 = 25 − 25 = 0 en f (8) = 25 − 8 2 = 25 − 64 = −39 en dat bestaat niet
Wat onder het wortelteken staat moet groter dan of gelijk aan 0 zijn.
Oplossen van 25 − x 2 = 0 geeft x = 5 of x = −5 .
Voor waarden van x tussen –5 en 5 is 25 − x 2 positief en voor waarden van x kleiner
dan –5 of groter dan 5 is 25 − x 2 negatief.
Het domein van deze functie is −5 ≤ x ≤ 5 .
y
6
5
Ui
tg
ev
f (2) = 25 − 2 2 = 25 − 4 = 21 ≈ 4, 48 , f (3) = 25 − 32 = 25 − 9 = 16 = 4 ,
f (x) = 25 – x 2
A
4
3
2
1
g
h
d
e
f
–4
–3
–1 O
–1
–2
zijde
5
6
x
kwadraat
9
16 +
AB = 4
OA = ...
25
Dus OA = 25 = 5 en dat klopt.
or
4
3
Het bereik van f is 0 ≤ y ≤ 5 .
De straal van deze cirkel is 5.
Zie de tekening hierboven.
Van punt O naar punt B moet je horizontaal 3 naar rechts en van punt B naar punt A
moet je verticaal 4 omhoog, dus de hoek bij punt B is een rechte hoek.
OB = 3
B
2
1
dh
–5
off
–6
39a
6
y
4
No
2
–5 –4 –3 –2
–1 O
–2
–4
–6
1
2
3
4
5
x
f (x) = 2x – 6
–8
–10
©
–12
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 17
–14
⁄
17
28-04-09 16:48
er
sb
v
Hoofdstuk 1 - Functies
y
2
b
1
–10 –8 –6 –4
–2 O
–1
2
4
6
8
10
x
–2
–3
–4
h (x) = – 6 + x2
–5
ev
–6
–7
–8
–9
–10
e
40a
b
c
41a
Ui
tg
Tussen de weerstand en de oppervlakte van de doorsnede van de draad bestaat een
omgekeerd evenredig verband.
0, 2
A
0, 2 1
Invullen van A = 6 geeft R(6) =
=
. De weerstand van de draad is
6
30
R( A) =
35
p in procenten
d
De gekozen waarden zijn a = 3 en b = −12 .
Invullen van x = 1 en y = 1 geeft 1 = a × 1 + b oftewel a + b = 1 . Het punt (1, 1) ligt
op de grafiek van f voor alle getallen a en b waarvoor geldt dat a + b = 1 .
Invullen van x = 1 en y = 1 geeft 1 = a × 12 + b oftewel a + b = 1 . Het punt (1, 1) ligt
op de grafiek van g voor alle getallen a en b waarvoor geldt dat a + b = 1 .
Invullen van x = 1 en y = 1 geeft 1 = b + a oftewel a + b = 1 . Het punt (1, 1) ligt op
1
de grafiek van h voor alle getallen a en b waarvoor geldt dat a + b = 1 .
Invullen van x = 1 en y = 1 geeft 1 = a ⋅ b × 1 − c oftewel a ⋅ b − c = 1 . Het punt (1, 1)
ligt op de grafiek van i voor alle getallen a en b waarvoor geldt dat a ⋅ b − c = 1 .
off
c
30
25
20
15
5
b
c
10
20
30
40
50
60
70 80
h in cm
90
p( h) = 320
h
320 = 5
320 = 10
h
h
h = 64
h = 32
De hoogte boven de grondwaterstand moet tussen de 32 cm en de 64 cm liggen. De
wortels van deze planten moeten tussen de 90 − 64 = 26 cm en de 90 − 32 = 58 cm in
de grond gestopt worden.
©
0
No
Ohm.
or
10
0
1
30
dh
⁄
18
1COLOR_INF_9789001606657_BW.indd 18
© Noordhoff Uitgevers bv
28-04-09 16:48
ICT Gebroken functies
I-1a
lengte l in cm
breedte b in cm
1
2
3
4
6
12
12
6
4
3
2
1
10
9
8
7
6
ev
breedte b in cm
fi
5
4
3
1
0
d
e
I-2a
d
e
I-3a
c
d
e
f
b
c
5
6
7
8
9
lengte l in cm
10
De lengte en de breedte van deze rechthoek zijn omgekeerd evenredig want
lengte keer breedte moet 12 zijn.
Omdat l ⋅ b = 12 , geldt b = 12 .
l
b(l ) = 12
l
b(100) = 0, 12 ; b(10) = 1, 2 ; b(1) = 12 ; b(0, 1) = 120 en b(0, 01) = 1200
Het domein van de functie b is ⟨0, →⟩ en het bereik van b is ⟨0, →⟩ .
Volgens de grafiek is haar gemiddelde snelheid 15 km per uur.
Hij moet dan met een gemiddelde snelheid van 12 km per uur rennen.
Als je 60 km per uur rijdt doe je 0,5 uur over die afstand.
Je moet de formule y = c kiezen, want de tijd en de snelheid zijn omgekeerd
x
evenredig.
De formule v = 30 geeft het verband tussen v en t.
t
Als x = 1 dan is y = 4 . Als x = 0, 5 dan is y = 8 .
Als y = 0, 5 dan is x = 8 . Als y = 0, 1 dan is x = 40 .
Bij de grafiek hoort de formule y = 4 .
x
Invullen van x = 0 geeft y = 4 , maar je kunt niet delen door 0.
0
Voor negatieve waarden van x krijg je net zo’n grafiek, maar met allemaal negatieve
uitkomsten.
©
b
4
off
3
dh
c
2
or
1
No
b
0
Ui
tg
2
er
sb
v
Hoofdstuk 1 - Functies
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 19
⁄
19
28-04-09 16:48
I-4a
x
0
1
2
y
–2
–3
–6
2,9
3
3,1
6
100
–60 kan niet
60
2
0,06
er
sb
v
Hoofdstuk 1 - Functies
b
c
d
6 = 6 = −2 en dat bestaat gewoon.
0 − 3 −3
Invullen van x = 3 geeft f (3) = 6 = 6 en dat bestaat niet.
3−3 0
Als x steeds groter wordt, dan naderen de uitkomsten naar 0.
e
Als x steeds kleiner wordt, dan naderen de uitkomsten ook naar 0.
f
Invullen van x = 0 geeft f (0) =
6 = −1000 geeft x − 3 = −0, 006 , dus x = 2, 994 .
x−3
Bijvoorbeeld voor x = 2, 995 is de uitkomst kleiner dan –1000.
I-5a
a=3
De grafiek bij een negatief getal is gespiegeld ten opzichte van de x-as of de y-as.
Voor a = 6 gaat de grafiek door het punt (2, 3).
I-6a
b
I-7a
d
I-8a
c
I-9a
b
d
b
d
ev
Ui
tg
De waarde x = 2 hoort bij de grafiek op het scherm niet tot het domein.
De coördinaten van het snijpunt met de x-as zijn (4, 0) en de coördinaten van het
snijpunt met de y-as zijn (0, –2).
Een formule van de horizontale asymptoot is y = −1 .
Een formule van de verticale asymptoot is x = −1 en een formule van de horizontale
asymptoot is y = −1 .
Op het moment dat het blikje in de koelkast wordt gezet is de temperatuur van het
blikje 24 C.
Na 57 minuten is de temperatuur 5 C.
Op den duur wordt de temperatuur van de cola 4 C.
Dat betekent dat de grafiek van T een horizontale asymptoot heeft.
De grafiek zou een verticale asymptoot kunnen hebben als de noemer gelijk is aan 0,
maar dan moet gelden t + 3 = 0 oftewel t = −3 en een negatieve tijd kan niet.
©
c
off
c
a=4
De functie f bestaat in dit geval niet voor x = 2 .
Als x heel dicht bij 2 in de buurt komt, dan worden de uitkomsten heel erg groot of
heel erg klein.
Voor a = 6 bestaat de functie niet voor x = 6 en als x heel dicht bij 6 in de buurt
komt, dan worden de uitkomsten heel erg groot of heel erg klein.
Voor a = −6 bestaat de functie niet voor x = −6 en als x heel dicht bij –6 in de buurt
komt, dan worden de uitkomsten heel erg groot of heel erg klein.
dh
b
De formule y = 120 hoort bij tabel A.
x
−1000
De formule y =
hoort bij tabel B, de formule y = 15 − 0, 6 x hoort bij tabel C,
x
14, 4
de formule y =
hoort bij tabel D, de formule y = 6 x − 18 hoort bij tabel E en de
x
formule y = −60 hoort bij tabel F.
x
or
c
No
b
Eerst oplossen van
⁄
20
1COLOR_INF_9789001606657_BW.indd 20
© Noordhoff Uitgevers bv
28-04-09 16:48
er
sb
v
Hoofdstuk 1 - Functies
Test jezelf
T-1a
f (−2) = −2 × −2 + 1 = 5 , f (1) = −2 × 1 + 1 = −1 , g(0, 5) = 0, 52 − 2 = 0, 25 − 2 = −1, 75 en
g(−3) = (−3)2 − 2 = 9 − 2 = 7
b
10
y
8
g
6
ev
4
2
–5
–4
–3
–2
–1 O
–2
1
2
–4
e
f
T-2a
Ui
tg
d
x
−2 x + 1 = 142
−2 x = 141
x = −70, 5
x 2 − 2 = 142
x 2 = 144
x = 12 of x = −12
De coördinaten van de snijpunten zijn (–3, 7) en (1, –1). Invullen van x = −3 geeft
f (−3) = −2 × −3 + 1 = 7 en g(−3) = (−3)2 − 2 = 9 − 2 = 7 en dat klopt. Invullen van x = 1
geeft f (1) = −2 × 1 + 1 = −1 en g(1) = 12 − 2 = 1 − 2 = −1 en dat klopt.
Invullen van x = 10 geeft g(10) = 10 2 − 2 = 100 − 2 = 98 .
Nee, de grafiek van g gaat niet door het punt (10, 102).
x
–4
–3
y
–12
–5
b
–2
–1
0
1
2
0
3
4
3
0
6
y
4
2
–5
–4
–3
off
5
–2 –1 O
–2
–4
4
–5 –12
1
2
3
4
5
x
or
–6
3
dh
c
4
f
–6
3
–8
f
–10
–12
c
d
Het bereik van f is ⟨←, 4 ] .
No
–4
–2
–1
©
–3
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 21
0
1
2
3
4
5
6
⁄
21
28-04-09 16:48
T-3a
b
er
sb
v
Hoofdstuk 1 - Functies
Het domein bij deze functie is [−4, →⟩ en het bereik bij deze functie is [ 3, →⟩ .
7
y
6
f
5
4
3
2
–5
c
d
T-4a
–3
–2
–1 O
–1
1
2
3
4
5
x
3+ x + 4 = 6
x+4 = 3
x+4 = 9
x=5
Invullen van x = 21 en y = 10 geeft 10 = a + 21 + 4 oftewel 10 = a + 5 , dus a = 5 .
De variabelen x en y zijn recht evenredig.
Een formule bij de tabel is y = 4 23 x .
b
De variabelen a en b zijn omgekeerd evenredig.
c
De formules daarbij zijn a × b = 6 , a = 6 en b = 6 .
b
a
De variabelen x en y zijn geen van beide.
off
Ui
tg
–4
ev
1
Een formule bij de tabel is y = 2 12 x + 1 .
d
De variabelen x en y zijn omgekeerd evenredig.
b
c
x
–1
y
− 12
0
−
2
3
1
2
–1
–2
2 12
3
3 12
4
5
–4 kan niet
4
2
1
De functie f bestaat niet voor x = 3 .
Als x heel dicht bij 3 in de buurt komt worden de uitkomsten heel erg groot positief
of heel erg groot negatief.
or
T-5a
dh
De formules daarbij zijn x × y = 120 , y = 120 en x = 120 .
x
y
d/e
4
y
3
f
No
2
1
–3
–2
–1 O
–1
1
2
3
4
5
6
7
x
–2
–3
–4
f
De formule bij de verticale asymptoot is x = 3 en de formule bij de horizontale
asymptoot is y = 0 .
©
⁄
22
1COLOR_INF_9789001606657_BW.indd 22
© Noordhoff Uitgevers bv
28-04-09 16:48
De functie f is een wortelfunctie, het domein is ⟨←, 4 ] en het bereik is ⟨←, 1] .
De functie g is een kwadratische functie, het domein zijn alle getallen en het bereik is
⟨←, 3] .
De functie h is een lineaire functie, het domein zijn alle getallen en het bereik zijn
alle getallen.
De functie l is een gebroken functie, het domein zijn alle getallen behalve x = 2 en
het bereik zijn alle getallen behalve y = 0 .
b
y
8
ev
T-6a
er
sb
v
Hoofdstuk 1 - Functies
7
6
5
4
h
2
1
–5
–4
–3
–2
–1 O
–1
f
1
2
3
4
5
x
–2
–3
c
De coördinaten van dat punt lijken (3, 0) te zijn. Invullen van x = 3 geeft
f (3) = 1 − 4 − 3 = 1 − 1 = 0 en h(3) = 6 − 2 × 3 = 0 en dat klopt.
T-7a
2
y
1
–7
–6
–5
–4
–3
–2
–1 O
–1
–2
–3
2
3
x
f
dh
–4
1
off
Ui
tg
3
–5
–6
–7
c
Een formule van de verticale asymptoot is x = −3 en een formule van de horizontale
asymptoot is y = −3 .
De waarde is a = 2 . In de grafiek zie je dat de functie niet bestaat voor x = 2 .
De functie bestaat niet als de noemer gelijk is aan 0, dus als x − a = 0 .
or
b
©
No
© Noordhoff Uitgevers bv
1COLOR_INF_9789001606657_BW.indd 23
⁄
23
28-04-09 16:48