IP opdracht “Hoogspringer”

IP opdracht “Hoogspringer”.
Lever een verslag in met de beantwoording van de genoemde vragen/opdrachten!
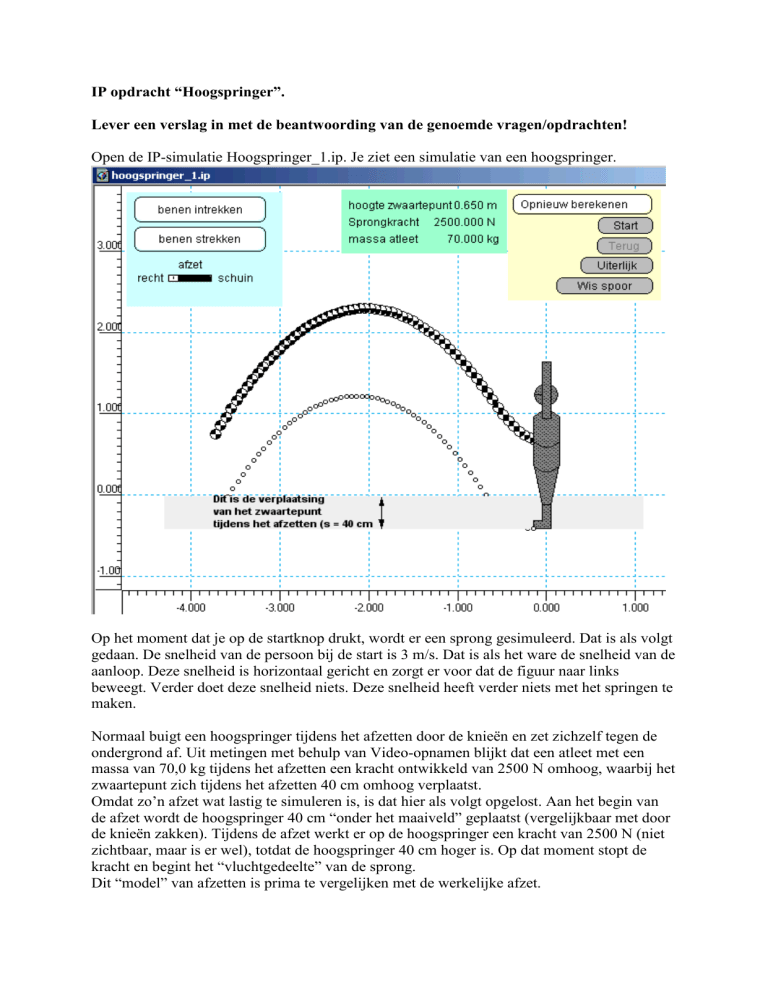
Open de IP-simulatie Hoogspringer_1.ip. Je ziet een simulatie van een hoogspringer.
Op het moment dat je op de startknop drukt, wordt er een sprong gesimuleerd. Dat is als volgt
gedaan. De snelheid van de persoon bij de start is 3 m/s. Dat is als het ware de snelheid van de
aanloop. Deze snelheid is horizontaal gericht en zorgt er voor dat de figuur naar links
beweegt. Verder doet deze snelheid niets. Deze snelheid heeft verder niets met het springen te
maken.
Normaal buigt een hoogspringer tijdens het afzetten door de knieën en zet zichzelf tegen de
ondergrond af. Uit metingen met behulp van Video-opnamen blijkt dat een atleet met een
massa van 70,0 kg tijdens het afzetten een kracht ontwikkeld van 2500 N omhoog, waarbij het
zwaartepunt zich tijdens het afzetten 40 cm omhoog verplaatst.
Omdat zo’n afzet wat lastig te simuleren is, is dat hier als volgt opgelost. Aan het begin van
de afzet wordt de hoogspringer 40 cm “onder het maaiveld” geplaatst (vergelijkbaar met door
de knieën zakken). Tijdens de afzet werkt er op de hoogspringer een kracht van 2500 N (niet
zichtbaar, maar is er wel), totdat de hoogspringer 40 cm hoger is. Op dat moment stopt de
kracht en begint het “vluchtgedeelte” van de sprong.
Dit “model” van afzetten is prima te vergelijken met de werkelijke afzet.
De grote punten (zwart-wit) stelt de baan van het zwaartepunt voor. Verder is er onderaan de
voet een extra meetpunt bevestigd waarvan ook de baan getoond wordt.
Luchtweerstand wordt steeds verwaarloosd!
Vraag 1
a. Bereken de arbeid tijdens de afzet.
b. Bereken (met behulp van de potentiële energie) de maximale hoogte die de
hoogspringer zou krijgen als deze een puntmassa was (als je verder geen rekening
houdt met de afmetingen).
 Simulatie 1
Start nu de simulatie (en doe verder nog niets!)
Vraag 2
a. Wat is de maximale hoogte van de onderkant van de voet?
b. Wat is de maximale hoogte van het zwaartepunt?
c. Vergelijk je antwoorden van 2 a en b met 1 b en geef een duidelijk commentaar c.q.
toelichting.
 Simulatie 2
Klik bij de simulatie op “opnieuw berekenen” en start de simulatie nogmaals.
Houdt nu meteen ná de afzet de knop “benen intrekken” ingedrukt totdat de springer
een soort hurkhouding heeft. Als hij over zijn hoogste punt is kun je de benen weer
strekken door de andere knop in te drukken.
Doe het eventueel enkele malen over.
Vraag 3
a. Vergelijk de baan van het zwaartepunt bij simulatie 1 en 2?
Leg uit/geef een verklaring.
b. Als de hoogspringer over een lat moet springen. In welk situatie (simulatie 1 of 2) kan
hij dan ‘het hoogst’ springen? Leg uit.
 Simulatie 3
Klik bij de simulatie op “opnieuw berekenen” en zet dan de knop afzet op “schuin”.
Op deze manier krijgt de springer tijdens de afzet een kleine rotatie mee, waardoor hij
als het ware een soort duiksprong maakt. Verdfer verandert er niets, dus ook niet aan
de arbeid tijdens de afzet. Start de simulatie.
Vraag 4
a. Vergelijk de baan van het zwaartepunt bij simulatie 1 en 2?
Leg uit/geef een verklaring.
b. Als de hoogspringer over een lat moet springen. In welk situatie (simulatie 1 of 2 of 3)
kan hij dan ‘het hoogst’ springen? Leg uit.
c. Ga er van uit dat de arbeid tijdens de afzet al maximaal is. Wat is volgens jou dan de
maximale hoogte die deze hoogspringer kan overwinnen, wat voor sprongtechniek hij
ook gaat verzinnen? Leg uit.
Blijkbaar is hoogspringen vooral een kwestie van de juiste techniek. Natuurlijk is
sprongkracht en afzet ook belangrijk, maar eenmaal “in de lucht” ligt de baan van het
zwaartepunt vast en is het een zaak om met je lichaam zo te bewegen dat je een maximale
hoogte kan overwinnen.
Nu lijkt dat de maximale hoogte van het zwaartepunt ook het maximaal haalbare is. Maar dat
is niet juist! Geoefende hoogspringers kunnen met een speciale techniek (b.v. de ruggelingse
“fosbury-flop”) zelf hoger springen “dan hun zwaartepunt”.
Geloof je het niet?
Open nu simulatie fosbury_goed.ip
 Druk nu NIET eerst op iets anders, maar druk meteen op Start en doe verder niets.
Deze simulatie is opgeslagen met een geslaagde opname.
De sprong wordt nu ruggelings uitgevoerd. Door tijdens de vlucht armen, rug en
benen op de juiste manier te bewegen, lukt het zelfs om in het hoogste punt de rug
hoger te hebben dan het zwaartepunt. Het zwaartepunt gaat misschien wel net onder
de lat door, maar het lichaam gaat er overheen!
Vraag 5
a. Leg uit hoe het kan dat je met een goede fosbury-flop toch iets hoger kunt springen
dan je eigen zwaartepunt.
 Probeer zelf ook een fosbury-flop te maken met de simulatie. Kies daarvoor eerst
“Opnieuw berekenen”. Waarschijnlijk gaat het het beste om de simulatie steeds even
stil te zetten, iets te wijzigen met de schuifknoppen, een stukje verder, weer iets
aanpassen, enz. Als je dan klaar bent, zet je de simulatie terug en kies je voor start.
Alle stappen worden nu achter elkaar getoond in een vloeiende simulatie.