Imaginaire getallen

Imaginaire getallen
Voor het oplossen van een negatieve wortel moeten de wiskundige eerst een getal maken.
Dit getal moest gelijk zijn aan  1 . De wiskundigen zijn op het getal i gekomen. Het
getal i komt van imaginair. Maar er zijn ook mensen die denken dat het gekozen is
omdat het veel op het getal 1 lijkt.
Het getal i is dus  1 . Het kwadraat van i is dus het kwadraat van  1 . Bij het
kwadrateren van een wortel haal je gewoon het wortelteken weg. Het getal i 2 is dus -1.
Dit lijkt vreemd omdat alle kwadraten van de reële getallen positief zijn. Dit komt omdat
een positief getal keer een positief getal positief blijft en een negatief getal keer een
negatief getal positief wordt. Er zijn dus geen negatieve kwadraten.
Je kunt met het getal i dus negatieve wortels berekenen. De wortel van -4 kun je
berekenen door:
x  4
x  1  4
x  i2
x  2i
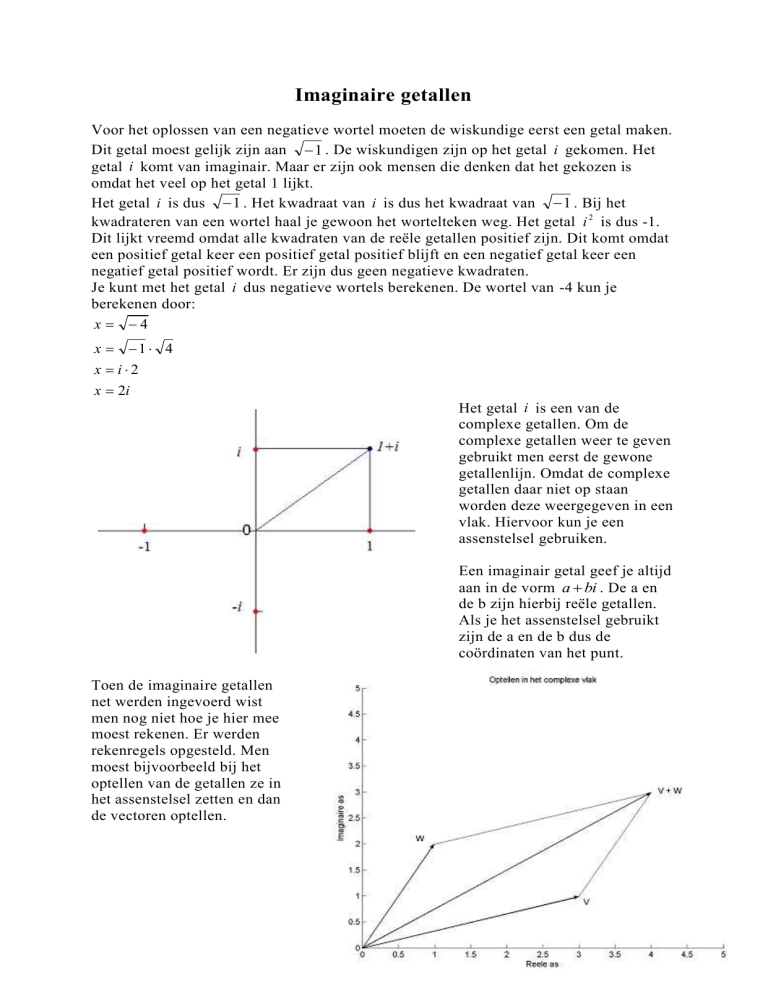
Het getal i is een van de
complexe getallen. Om de
complexe getallen weer te geven
gebruikt men eerst de gewone
getallenlijn. Omdat de complexe
getallen daar niet op staan
worden deze weergegeven in een
vlak. Hiervoor kun je een
assenstelsel gebruiken.
Een imaginair getal geef je altijd
aan in de vorm a  bi . De a en
de b zijn hierbij reële getallen.
Als je het assenstelsel gebruikt
zijn de a en de b dus de
coördinaten van het punt.
Toen de imaginaire getallen
net werden ingevoerd wist
men nog niet hoe je hier mee
moest rekenen. Er werden
rekenregels opgesteld. Men
moest bijvoorbeeld bij het
optellen van de getallen ze in
het assenstelsel zetten en dan
de vectoren optellen.
Met de imaginaire getallen kun je dus berekenen dat de vergelijking x 2  2 x  5  0 de
oplossing x  1 2i heeft. Dit kun je weer controleren door x  1 2i in te vullen in de
vergelijking en kijken of het antwoord x  0 wordt.
x  1 2i invullen in x 2  2 x  5  0 geeft
2
y   1  2i   2 1  2i   5
y   1  2i  1  2i   2 1  2i   5
y  1  4i  4i 2  2  4i  5
y  4i 2  4
i 2 kan vervangen worden door -1
y  4  1  4
y0
Dus x  1 2i is inderdaad een oplossing van de vergelijking x 2  2 x  5  0 .
Nu kun je met de ABC-formule berekenen of er nog andere oplossing zijn.
a  1 , b  2 en c  5
D  2 2  4 1  5
D  4  20
D  16
Ondanks dat de discriminant kleiner is dan nul kun je nog steeds de snijpunten
uitrekenen. Dit kan omdat je nu weet hoe de imaginaire getallen werken.
 2   16
 2   16
x1 
 x2 
2 1
2 1
 2   1  16
 2   1  16
x1 
 x2 
2 1
2 1
 2 i4
 2 i4
x1 
 x2 
2
2
 2  4i
 2  4i
x1 
 x2 
2
2
x1  1  2i  x2  1  2i
Dus de andere oplossing van de vergelijking x 2  2 x  5  0 is x  1 2i .