cursus sommeren

²
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 1/7
sommeren en integreren
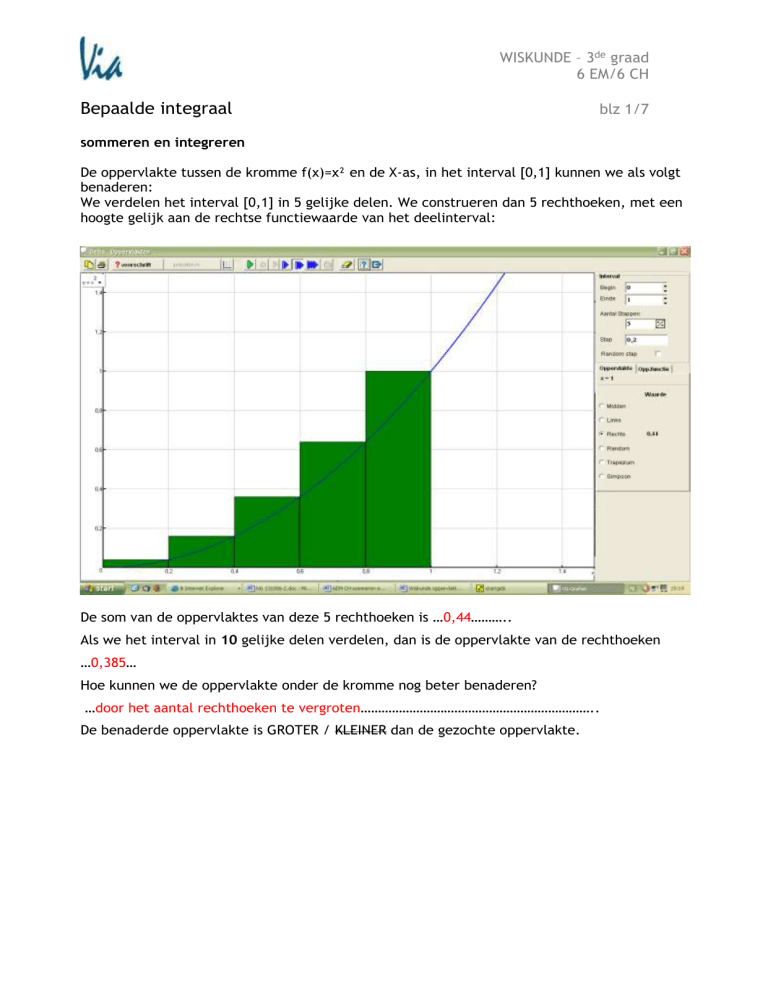
De oppervlakte tussen de kromme f(x)=x² en de X-as, in het interval [0,1] kunnen we als volgt
benaderen:
We verdelen het interval [0,1] in 5 gelijke delen. We construeren dan 5 rechthoeken, met een
hoogte gelijk aan de rechtse functiewaarde van het deelinterval:
De som van de oppervlaktes van deze 5 rechthoeken is …0,44………..
Als we het interval in 10 gelijke delen verdelen, dan is de oppervlakte van de rechthoeken
…0,385…
Hoe kunnen we de oppervlakte onder de kromme nog beter benaderen?
…door het aantal rechthoeken te vergroten…………………………………………………………..
De benaderde oppervlakte is GROTER / KLEINER dan de gezochte oppervlakte.
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 2/7
Nemen we nu dezelfde grafiek, maar we construeren de rechthoeken met een hoogte gelijk
aan de linkse functiewaarde van het deelinterval:
De som van de oppervlaktes van deze 5 rechthoeken is …0,24……………..
Als we het interval in 10 gelijke delen verdelen, dan is de oppervlakte van de rechthoeken
…0,285…
De benaderde oppervlakte is GROTER / KLEINER dan de gezochte oppervlakte.


De ondersom is de som van de oppervlakten van de rechthoeken die onder de kromme
gelegen zijn.
De bovensom is de som van de oppervlakten van de rechthoeken die boven de kromme
gelegen zijn.
WISKUNDE – 3de graad
6 EM/6 CH
²
Bepaalde integraal
blz 3/7
De oppervlakte A van het gebied tussen de grafiek f(x) en de X-as over het interval [a,b]
kunnen we dus benaderen met n rechthoeken.
De basis van elk rechthoekje is x, dit is het n-de deel van het interval [a,b].
De oppervlakte van al deze rechthoekjes is gelijk aan de som:
f(x1).x + f(x2).x + f(x3).x + … + f(xn).x
n
 f(xi ).x
Dit noteren we:
.
i1
Het optellen van een eindig aantal oppervlakten noemen we sommeren. De oppervlakte A
kunnen we zo dicht mogelijk benaderen door het aantal rechthoeken n te verhogen.
OEFENING 1
Start programma Delta-T5/6 op
Kies: VU-grafiek – openen –
VU-grafiek PLUS
-
oppervlakten
We tekenen de grafiek f(x)=0,5 x²+1, in het interval [0,4]
- Bereken onder- en bovensom voor n=8 en n=40:
n=8
n=40
ondersom
12,75
ondersom
14,27
bovensom
16,75
bovensom
15,07
- Bereken nu de juiste oppervlakte door de oppervlaktefunctie te berekenen:
f(x) = 0.5x²+1
F(x) =
interval [0,4]
0.5x³
+x+c
3
F(0) = 0

x³
+x+c=0
6
Oppervlaktefunctie A(x) =
A(4) =

c=0
x³
+x
6
4³
64  24
+4=
= 14,667
6
6
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 4/7
MACHINEREKENEN - TEXAS INSTRUMENTS
Stap 1: maak een rij van de functiewaarden:
[2nd] [LIST] [] [5:seq]
0.5x²+1 [,] x [,] 0 [,] 3.5 [,] 0.5 [)] [ENTER]
Stap 2: maak een rij van oppervlakken:
[x] 0.5 [ENTER]
Stap 3: sommeer deze oppervlakken:
[2nd] [LIST] [] [] [5:sum]
[2nd] [ANS] [ENTER]
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 5/7
OEFENING 2
Benader de volgende oppervlaktes door je grafische rekenmachine te gebruiken:
Benader de oppervlakte van het gebied tussen de grafiek en de X-as over het gegeven interval,
waarvan de rechterbovenhoeken op de grafiek van f liggen.
f(x)=x³
[0,2]
n=20
A = …4,41…………………….
f(x)=x4
[1,2]
n=10
A = …6,973………………….
f(x)=-0,01x³+2x
[1,4]
n=30
A = …14,63…………………….
Benader nu de oppervlakte van het gebied tussen de grafiek en de X-as over het gegeven
interval, waarvan de linkerbovenhoeken op de grafiek van f liggen.
f(x)=x³
[0,2]
n=20
A = …3,61…………………….
f(x)=x4
[1,2]
n=10
A = …5,473………………….
f(x)=-0,01x³+2x
[1,4]
n=30
A = …12,779………………….
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 6/7
Als we de oppervlakten van de n rechthoeken in
de volgende figuur optellen, bekomen we een
benadering van de oppervlakte onder de grafiek
van de veeltermfunctie en de X-as.
n
 f(xi ).x
Deze som noteren we:
i1
Als we de breedte x van de rechthoeken
verkleinen en bijgevolg het aantal rechthoeken
laten toenemen, dan nadert deze som steeds
dichter tot de oppervlakte A van het gebied.
We noteren:
A=
n
 f(xi ).x
met x  0
i1
integraalnotatie:
b
A=  f( x)dx
a
0
a
b
Het optellen van een oneindig aantal oppervlakten noemen we integreren.
We noemen
b
 f(x)dx
de bepaalde integraal van de functie f tussen de grenzen a en b.
a
De getallen a en b heten resp. de ondergrens en bovengrens van de integraal.
OEFENING 3
Schrijf de oppervlakte van het ingekleurde gebied tussen de grafiek van de gegeven functies
met de X-as met de integraalnotatie:
f(x)= - x² + 4x
3
A= ……  ( x²  4x).dx ……………
0
f(x)= -x³ + 2x + 3
A= ……
2
 (x³  2x  3).dx ………
 0.5
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 7/7
f(x)= x³
2
A= …  x².dx …………………
1
f(x)= x² - 4x + 3
0.5
A= …  ( x²  4x  3).dx ……………
1
WISKUNDE – 3de graad
6 EM/6 CH
Bepaalde integraal
blz 4/7
MACHINEREKENEN - CASIO
Stap 1:
Voer in de modus TABLE de functie f(x)=0.5x²+1
In de tabel berekenen we de functiewaarden vanaf
x1=0,1 tot en met x10=4 met stapgrootte 0,5
Daarna roepen we menu LIST op en leggen met de
optie LMEM de Y1-kolom van de tabel vast in lijst 1:
[MENU] [7:TABLE] x² [EXE]
[F5:RANG] 0.1 [EXE] 4 [EXE] 0.5 [EXE] [EXIT]
[F6:TABLE] [:kolom Y1] [OPTN] [F1:LIST]
[F2:LMEM] [F1:List1]
Stap 2:
In de modus LIST vermenigvuldigen we elke
functiewaarde in lijst 1 met de breedte x=0,5 van de rechthoeken en bekomen zo lijst 2 met
de oppervlakten van de 8 rechthoeken.
[MENU] [4:LIST] [] [] [OPTN] [F1:LIST] [F1:List] 1 [x] 0.5 [EXE]
Stap 3:
Om de som van de oppervlakten van de rechthoeken te berekenen, kiezen we voor optie Sum
(sommatie) uit het optiemenu LIST.
[] [F6:] [F6:] [F1:Sum] [F6:] [F1:LIST] 2 [EXE]