Zelftoets hoofdstuk 2

4 Vwo
Vathorst College
Zelftoets
Hoofdstuk 2
In deze zelftoets wordt geen aandacht besteedt aan de oppervlaktemethode en raaklijnmethode. Wil je daarmee oefenen,
bekijk dan daarvoor nogmaals de opgaven uit het boek.
1
Nettokracht
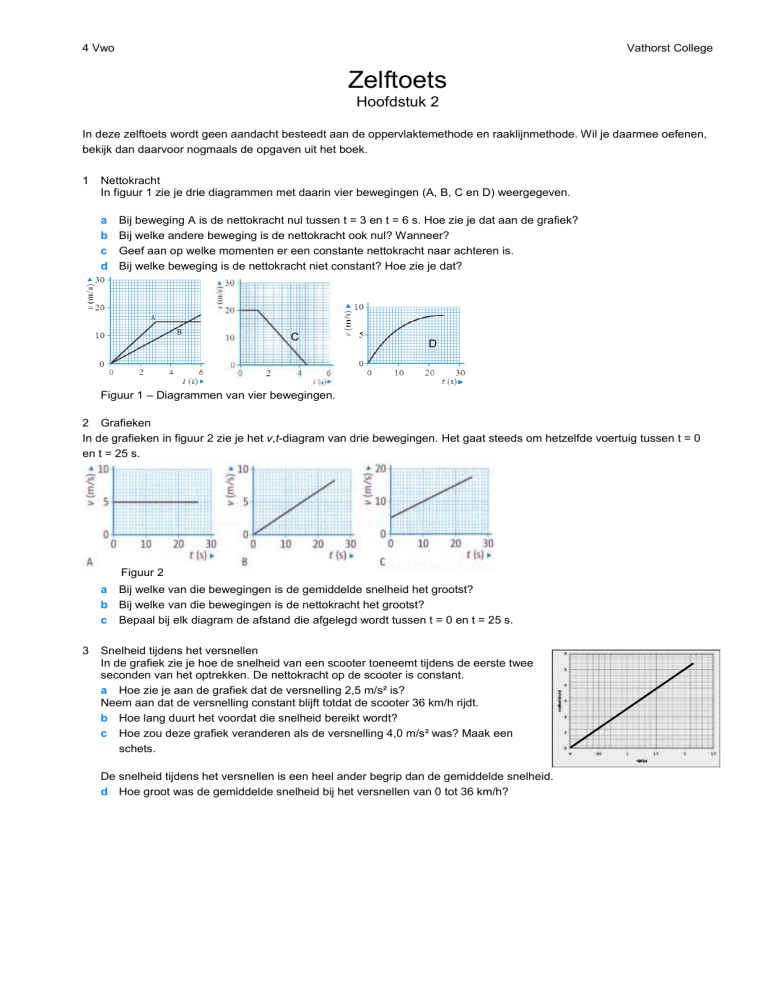
In figuur 1 zie je drie diagrammen met daarin vier bewegingen (A, B, C en D) weergegeven.
a
b
c
d
Bij beweging A is de nettokracht nul tussen t = 3 en t = 6 s. Hoe zie je dat aan de grafiek?
Bij welke andere beweging is de nettokracht ook nul? Wanneer?
Geef aan op welke momenten er een constante nettokracht naar achteren is.
Bij welke beweging is de nettokracht niet constant? Hoe zie je dat?
C
D
Figuur 1 – Diagrammen van vier bewegingen.
2 Grafieken
In de grafieken in figuur 2 zie je het v,t-diagram van drie bewegingen. Het gaat steeds om hetzelfde voertuig tussen t = 0
en t = 25 s.
Figuur 2
a Bij welke van die bewegingen is de gemiddelde snelheid het grootst?
b Bij welke van die bewegingen is de nettokracht het grootst?
c Bepaal bij elk diagram de afstand die afgelegd wordt tussen t = 0 en t = 25 s.
3
Snelheid tijdens het versnellen
In de grafiek zie je hoe de snelheid van een scooter toeneemt tijdens de eerste twee
seconden van het optrekken. De nettokracht op de scooter is constant.
a Hoe zie je aan de grafiek dat de versnelling 2,5 m/s² is?
Neem aan dat de versnelling constant blijft totdat de scooter 36 km/h rijdt.
b Hoe lang duurt het voordat die snelheid bereikt wordt?
c Hoe zou deze grafiek veranderen als de versnelling 4,0 m/s² was? Maak een
schets.
De snelheid tijdens het versnellen is een heel ander begrip dan de gemiddelde snelheid.
d Hoe groot was de gemiddelde snelheid bij het versnellen van 0 tot 36 km/h?
4 Vwo
Vathorst College
4
Optrekkende fietser
Een fietser trekt vanuit stilstand 4,0 s lang op met een versnelling van 1,6 m/s².
a Welke afstand heeft de fietser na 4,0 s afgelegd?
b Is het s,t-diagram van deze beweging een dal- of een bergparabool?
5
Vier s,t-diagrammen
In figuur 4 zijn vier s,t-diagrammen weergegeven. Bij elke beweging is de nettokracht constant.
A
B
C
D
Figuur 4 – Vier afstand-tijd-diagrammen
a
b
c
d
e
6
Bij welk van deze bewegingen is de beginsnelheid nul? Leg uit.
Bij welk van deze diagrammen is de snelheid constant? Leg uit.
Bij welk van deze bewegingen is de nettokracht tegengesteld aan de richting van de snelheid? Leg uit.
Bij welk van deze bewegingen is de versnelling het grootst?
Bij welk van deze bewegingen is de gemiddelde snelheid (van t = 0 tot t = 6 s) het grootst?
Snelheid en vrije val
Een voorwerp voert vanuit stilstand een vrije val uit.
a Hoe groot is de versnelling van dat voorwerp na 3,5 s? En na 4,2 s?
b Hoe groot is de snelheidstoename van dat voorwerp tussen 3,6 en 5,6 s?
Het voorwerp valt 6,0 s.
c Hoe groot is de eindsnelheid?
7
Papieren kegeltje
Van papier wordt een kegeltje gevouwen (figuur 1). Als men het kegeltje laat vallen dan bereikt het al snel een
constante snelheid van 0,80 m/s. Het kegeltje heeft een massa van 0,15 g. voor de luchtwrijvingskracht geldt:
Fw,l = k·v².
a Bereken de zwaartekracht op het kegeltje.
b Bereken de waarde van k voor het kegeltje.
Vervolgens legt men drie identieke kegeltjes is elkaar.
c Leg uit dat de waarde van k hierdoor niet veranderd.
d Bereken welke constante snelheid de drie kegeltjes samen krijgen.
8
Een auto met een massa van 850 kg rijdt met een snelheid van 80 km/h over een weg. De wrijvingskracht is op dat
moment 112 N.
a Leg uit of de voorwaartse kracht op dat moment groter, kleiner, of gelijk is aan 112 N.
De automobilist remt waardoor de achterwaartse kracht op de auto, bij een snelheid van 80 km/h, er voor zorgt dat de
vertraging van de auto gelijk is aan 8,2 m/s2.
b Bepaal de remkracht van de auto.
c Bereken binnen welke afstand de auto tot stilstand zou komen als de achterwaartse kracht op de auto gedurende
het vertragen constant zou blijven.
De reactietijd van de bestuurder is 1,1 s.
d Bereken de stopafstand van deze automobilist.