20o Fz Bij vraag 1 en 2

Kracht en Moment: blok op een helling en tafel met antwoorden
Blok op Helling
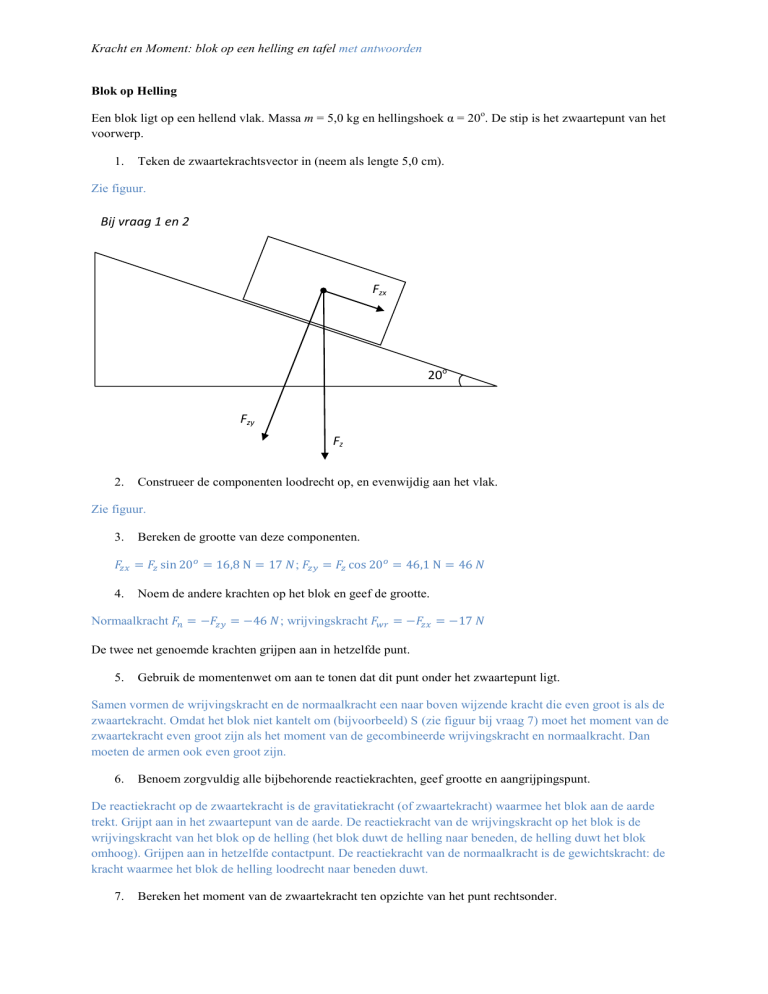
Een blok ligt op een hellend vlak. Massa m = 5,0 kg en hellingshoek α = 20o. De stip is het zwaartepunt van het
voorwerp.
1.
Teken de zwaartekrachtsvector in (neem als lengte 5,0 cm).
Zie figuur.
Bij vraag 1 en 2
Fzx
20o
Fzy
Fz
2.
Construeer de componenten loodrecht op, en evenwijdig aan het vlak.
Zie figuur.
3.
Bereken de grootte van deze componenten.
;
4.
Noem de andere krachten op het blok en geef de grootte.
Normaalkracht
; wrijvingskracht
De twee net genoemde krachten grijpen aan in hetzelfde punt.
5.
Gebruik de momentenwet om aan te tonen dat dit punt onder het zwaartepunt ligt.
Samen vormen de wrijvingskracht en de normaalkracht een naar boven wijzende kracht die even groot is als de
zwaartekracht. Omdat het blok niet kantelt om (bijvoorbeeld) S (zie figuur bij vraag 7) moet het moment van de
zwaartekracht even groot zijn als het moment van de gecombineerde wrijvingskracht en normaalkracht. Dan
moeten de armen ook even groot zijn.
6.
Benoem zorgvuldig alle bijbehorende reactiekrachten, geef grootte en aangrijpingspunt.
De reactiekracht op de zwaartekracht is de gravitatiekracht (of zwaartekracht) waarmee het blok aan de aarde
trekt. Grijpt aan in het zwaartepunt van de aarde. De reactiekracht van de wrijvingskracht op het blok is de
wrijvingskracht van het blok op de helling (het blok duwt de helling naar beneden, de helling duwt het blok
omhoog). Grijpen aan in hetzelfde contactpunt. De reactiekracht van de normaalkracht is de gewichtskracht: de
kracht waarmee het blok de helling loodrecht naar beneden duwt.
7.
Bereken het moment van de zwaartekracht ten opzichte van het punt rechtsonder.
Kracht en Moment: blok op een helling en tafel met antwoorden
Bij vraag 7
Fzx
rz
.S
20o
Fzy
Fz
Zie figuur voor de arm van de zwaartekracht. Je kunt de arm bepalen door of meten in de figuur als deze op
schaal is, of goniometrie gebruiken: zie de driehoeken in de figuur. Je vindt dan een arm van 3,84 cm. En een
moment van 1,88 Nm.
Ook Bij vraag 7
Fzx
rFy
. Sr
Fx
20o
Fzy
In de tweede figuur zie je een andere strategie: bereken de momenten van de componenten van de zwaartekracht
en tel deze op:
;
;
.
Stel je duwt de bovenste punt van het blok naar rechts, zo dat het blok net (niet) kantelt om het punt rechtsonder.
8.
Bereken de benodigde kracht.
Zie figuur.
Kracht en Moment: blok op een helling en tafel met antwoorden
Bij vraag 8
F
rF
F
rz
.S
20o
Op het moment van kantelen grijpen de wrijvingskracht en de normaalkracht aan in S, het enige contactpunt. Ten
opzichte van S hebben dan alleen F en Fz een moment dat niet nul is. De arm van F kan weer met goniometrie of
via meten in de figuur worden bepaald. Resultaat: F = 23,2 N.
De helling wordt gladder gemaakt. De maximale wrijvingskracht op het blok is nu 15,0 N.
9.
Bereken de versnelling van het blok.
;
10. Bereken hoe lang het blok erover doet om vanuit stilstand een snelheid van 1,3 m/s te bereiken.
Het blok versnelt eenparig omdat beide krachten niet veranderen:
.
Het blok wordt opgetild door het aan een touw omhoog te trekken. Het touw is zo bevestigd dat als het blok van
de helling af is, het blok netjes horizontaal hangt.
11. Bereken de arbeid die je moet verrichten om het blok net horizontaal te krijgen (het blok laat de helling
net los).
Bij vraag 11
sz
20o
Fz
Kracht en Moment: blok op een helling en tafel met antwoorden
Neem aan dat alleen de verticale hijskracht arbeid verricht. Dan is alleen de verticale verplaatsing van het
zwaartepunt van belang. Die bepaling kan weer met goniometrie of met meten in de figuur. Nieuwe hoogte
boven helling:
. Oude hoogte:
.
.
12. Bereken het vermogen dat nodig is om het blok vanaf deze positie met een snelheid van 1,5 m/s op te
hijsen.
Je verricht arbeid tegen de zwaartekracht:
Stel je gebruikt een losse katrol om te hijsen, zie figuur. Dan hoef je minder hard te trekken.
13. Verklaar deze werking van een los katrol met behulp van de momentenwet t.o.v. het meest rechtse punt
van deze katrol (massa katrol wordt verwaarloosd).
De arm van de zwaartekracht is de helft van de arm van de spankracht van het koord. Aangezien het
gezamenlijke moment nul moet zijn (bij beweging met constante snelheid), is de spankracht en dus de trekkracht
half zo groot als de zwaartekracht.
14. Hoeveel vermogen moet de trekkracht nu leveren?
Nog steeds 74 W! De kracht is gehalveerd, maar de verplaatsing (hoeveel touw je binnenhaalt) is verdubbeld.
Door wrijvingskracht aan de katrollen is het rendement van het hijsproces 85%.
15. Bereken de energie die nodig is om het gewicht 50 cm op te hijsen.
Nuttige arbeid:
;
.
16. Hoe groot is dan de kracht waarmee je aan het touw moet trekken?
Het touw moet dan 1,0 meter worden ingehaald:
.
Tafel
Hiernaast zie je een tafel getekend. Voor het gemak is deze tafel op zijn
kant getekend. Zwaartepunt Z ligt ergens op de stippellijn; x is de
onbekende afstand van onderkant blad tot Z. De massa van het
(homogene) blad is 15 kg, de (homogene) poten wegen samen 10 kg.
80 cm
17. Bereken x.
Moment linksom: (x+5)15 Moment rechtsom: (40-x)10. Dus: 15x+45
= 400-10x 25x = 355 ; x = 355/25 = 71/5 = 14,2 cm
x cm
Als je deze tafel echt op zijn kant zou zetten zoals in de tekening, zou deze
rechtsom kiepen tot de onderste poten de grond raken.
18. Hoe zwaar zouden de poten moeten zijn (bij gelijk formaat) opdat
de tafel in de getekende positie net (niet) zou kantelen?
Dan Z boven punt rechtsonder tafelblad: 15 x 5 = 40 x m; m = 75/40
= 3,75/2 = 1,875 = 1,9 kg.
EINDE
10 cm
Z