Vrienden zijn er om je te steunen

7.1 toenamediagrammen
Interval
Open interval: <○>  punten doen niet mee <-1,3>  -1 en 3 doen niet mee
Gesloten interval: [●]  punten doen wel mee [-1,3]  -1 en 3 doen wel mee
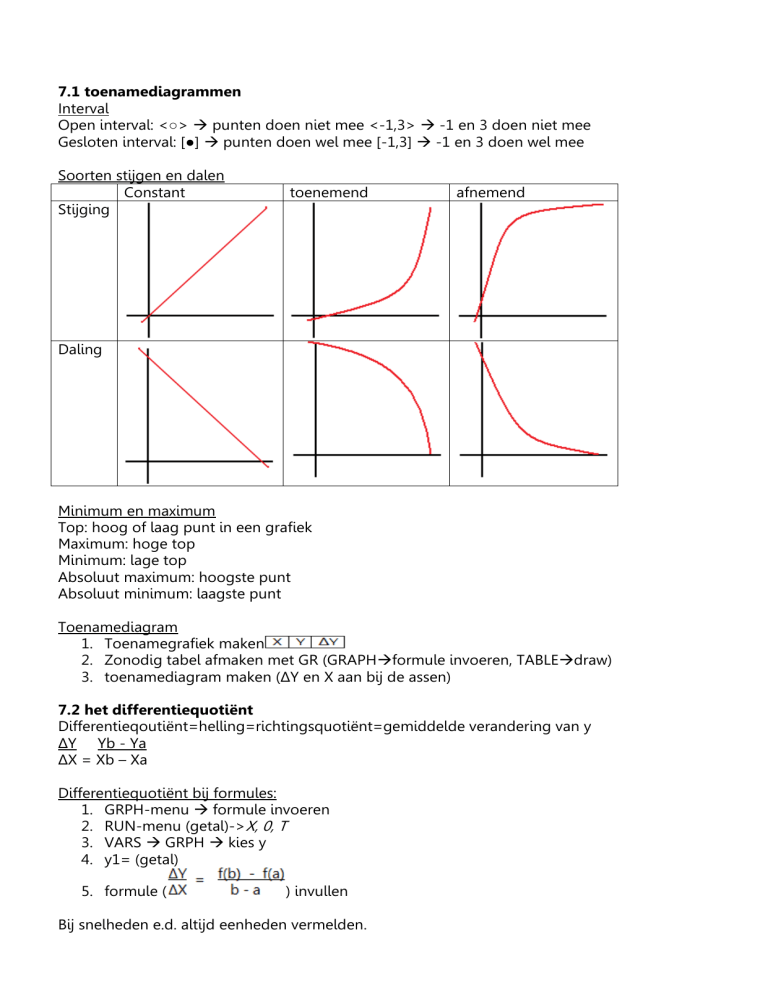
Soorten stijgen en dalen
Constant
Stijging
toenemend
afnemend
Daling
Minimum en maximum
Top: hoog of laag punt in een grafiek
Maximum: hoge top
Minimum: lage top
Absoluut maximum: hoogste punt
Absoluut minimum: laagste punt
Toenamediagram
1. Toenamegrafiek maken
2. Zonodig tabel afmaken met GR (GRAPHformule invoeren, TABLEdraw)
3. toenamediagram maken (ΔY en X aan bij de assen)
7.2 het differentiequotiënt
Differentieqoutiënt=helling=richtingsquotiënt=gemiddelde verandering van y
ΔY Yb - Ya
ΔX = Xb – Xa
Differentiequotiënt bij formules:
1. GRPH-menu  formule invoeren
2. RUN-menu (getal)->X, 0, T
3. VARS  GRPH  kies y
4. y1= (getal)
5. formule (
) invullen
Bij snelheden e.d. altijd eenheden vermelden.
7.3 raaklijnen en snelheden
Tijd-afstandformules:
1. GRPH-menu  formule invoeren
2. RUN-menu  OPTN  CALC  d/dx
3. VARS  GRPF  y kiezen
4. d/dx(y1,X) = antwoord
5. noteren als:
=richtingscoëfficiënt raaklijn A = snelheid waarmee y veranderd voor x=xA = de
helling van de grafiek in A
Formule raaklijn opstellen
1. GRPH-menu  formule invoeren
2. A uitrekenen via d/dx(y1,X)  zie tijdsafstandformules
3. formule opstellen (k: y=ax+b)
4. y1= oproepen met de gegeven X  zie differentiequotiënt bij formules
5. X en Y in formule invullen
6. B uitrekenen
7. formule opstellen (y = getal X + getal)
Wil je weten of y toe- of afneemt voor x=A, dan reken je d/dx uit met x=A. Blijkt dat:
-
>0
dan neemt de y toe voor x=A
-
<0
dan neemt de y af voor x=A
Verband tussen grafiek en hellingsgrafiek:
- grafiek stijgend: hellinggrafiek boven de X-as
- grafiek dalend: hellinggrafiek onder de X-as
- grafiek heeft top: hellinggrafiek snijdt de X-as
7.4 de afgeleide functie
Differentieregels:
- f(x) = ax²

f’(x) = 2ax¹
- f(x) = ax

f’(x) = 1×axº=a
- f(x) = a

f’(x) = 0
Eerst haakjes, dan ×en/, dan +enBvb.: f(x) = 6x³

f’(x) = 3×6x²=18x²
Stel met behulp van de afgeleide de formule van de raaklijn op
1. De afgeleide formule berekenen
2. Formule opstellen (bvb. m: y=ax+b)
3. Vul de XA in in de afgeleide formule en bereken hiermee de a
(bvb. Bij de functie f(x)=0,2x³-6x+2 met XA=5  a=f’(5)=0,6×5²-6=9)
4. Formule tot zover invullen (bvb. m: y=9x+b)
5. Dan vul je in de functie de XA voor de x in. Hiermee reken je de y uit, nu heb je de x
en de y (bvb. YA=f(XA=-3, dus A is (5, -3))
6. Reken de b uit door de x en de y in te vullen in de formule y=ax+b
7.5 toepassingen van de afgeleide
Notities voor de afgeleide
De afgeleide is
, dus als je de afgeleide op moet schrijven kun je ook
formule erachter opschrijven, bijvoorbeeld
met de
(3x²+8x) de uitkomst hiervan is de afgeleide,
dus 6x+8. Dit schrijf je zo op
(3x²+8x)= 6x+8.
Maar de beste manier om het op te schrijven is:
d(8x³+6x²)
dx
= 24x²+12x.
Als er onder de deelstreep bij
bijvoorbeeld dt staat i.p.v. dx moet je naar t
differentiëren. Als je de formule 24t²+12x hebt en je moet naar x differentiëren, dan krijg
je als afgeleide: 0+12.
Stijgen, dalen en toppen
Is f’(x)>0 op een interval, dan is f stijgend voor dat interval.
Is f’(x)<0 op een interval, dan is f dalend voor dat interval.
Berekenen van maxima en minima(extreme waarden)
Bij de opdracht
Bereken algebraïsch het maximum van y.
Moet je
1. de afgeleide
2. de vergelijking
berekenen
=0 algebraïsch oplossen
3. de grafiek van y schetsen en aflezen welke oplossing van
=0 bij het maximum
hoort
4. het maximum berekenen door de gevonden x-waarde in te vullen in de formule
van y.
Controleren van maxima en minima
Bij de opdracht
Toon met de afgeleide aan dat y een maximum heeft voor x=a.
Moet je
1. de afgeleide
berekenen en laten zien dat
=0
2. de grafiek van y schetsen en opmerken dat er inderdaad een hoogste punt is.
Par. 8.1 centrum- en spreidingsmaten
Med: Mediaan: Het middelste waarnemingsgetal als alle getallen naar grootte
gerangschikt zijn. Bij een even aantal waarnemingsgetallen is de mediaan het
gemiddelde van de twee middelste getallen.
Mod: Modus: Het waarnemingsgetal met de grootste frequentie
Modale klasse: klasse met de grootste frequentie
en μ:
Gemiddelde
n:
Aantal waarnemingsgetallen
xσn: σ: Het gemiddelde
minX: Kleinste waarnemingsgetal
Q1: Het 1e kwartiel
Q3: Het 3e kwartiel
maxX: Het grootste waarnemingsgetal
Voordeel
Modus
*Snel op te schrijven,
weinig rekenwerk
*De enige centrummaat
die bij kwalitatieve
gegevens te gebruiken is
Mediaan
*Niet gevoelig voor
uitschieters
*Weinig rekenwerk
Gemiddelde *Alle gegevens worden
gebruikt
Nadeel
*geeft weinig informatie
*is niet altijd aanwezig
*een kleine verandering kan een geheel
andere modus opleveren
*alleen de volgorde van de
waarnemingsgetallen is van belang, niet de
grootte van het verschil tussen de
waarnemingsgetallen
*gevoelig voor uitschieters
De boxplot:
De relatieve cumulatieve frequentiepolygoon kun je goed gebruiken om bij een
klassenindeling de mediaan te schatten. De relatieve cumulatieve frequentie van de
mediaan is namelijk 50%, dus:
- Begin op de verticale as bij 50
- Ga horizontaal naar de grafiek
- Lees op de horizontale grafiek de mediaan af
De mediaan verdeelt een serie waarnemingsgetallen in twee groepen, die elk bestaat uit
50% van de waarnemingsgetallen. Van elk van deze even grote groepen kun je weer de
mediaan bepalen. Er ontstaan van een verdeling in vier groepen die elk 25% van de
waarnemingsgetallen bevat.
De mediaan van de eerste helft heet het eerste kwartiel(Q1)links van mediaan(25%)
De mediaan van de tweede helft heet het derde kwartiel(Q3)rechts van mediaan(75%)
Samen met het kleinste en het grootste waarnemingsgetal gebruik je Q1, de mediaan en
Q3 bij het tekenen van een boxplot.
Spreidingsmaten:
Om een goede indruk te krijgen van een serie waarnemingsgetallen moet je behalve het
gemiddelde ook nog een getal hebben dat informatie geeft over de spreiding van de
getallen. Zo’n getal heet een spreidingsmaat. Er zijn verschillende spreidingsmaten in
gebruik.
- De spreidingsbreedte: het verschil tussen het grootste en kleinste
waarnemingsgetal
- De kwartielafstand: het verschil tussen het 3e en 1e kwartiel
Spreidingsbreedte = 8 – 1 = 7
Kwartielafstand = Q3 – Q1 = 6 – 3 = 3
De meest gebruikte spreidingsmaat is de standaardafwijking. Om de standaardafwijking te
berekenen moet je eerst van elk waarnemingsgetal berekenen hoe ver het van het
gemiddelde af ligt. Zo krijg je bij elk waarnemingsgetal x de deviatie d(de afwijking van
het gemiddelde). Dus d = x Par. 8.2 eigenschappen van de normale verdeling
Vuistregels bij de normale verdeling:
- 68% van alle waarnemingen
ligt tussen μ – σ en μ + σ
- 95% van alle waarnemingen
ligt tussen μ – 2σ en μ + 2σ
Normaal-waarschijnlijkheidspapier:
Bij de normale verdeling hoort:
- bij μ de relatieve cumulatieve frequentie 50
- bij μ + σ de relatieve cumulatieve frequentie 84
Op normaal-waarschijnlijkheidpapier lees je op de verticale as de relatieve cumulatieve
frequentie af. Op de horizontale as kun je zelf een geschikte lineaire schaalverdeling
kiezen om de klassen uit te zetten.
Stappenplan: hoe onderzoek je of bij een verdeling een normale benadering is toegestaan
en hoe schat je μ en σ?
1. bereken van elke klasse de relatieve cumulatieve frequentie.
2. zet deze relatieve cumulatieve frequenties uit op normaalwaarschijnlijkheidspapier, telkens boven de rechtergrens van de klasse
3. ga na of de punten bij benadering op een rechte lijn liggen
4. lees op de horizontale as μ af bij de relatieve cumulatieve frequentie 50
5. lees op de horizontale as μ + σ af bij de relatieve cumulatieve frequentie 84. hieruit
volgt σ.
Frequentie: aantal dingen in de frequentie
Cumulatieve frequentie: de frequentie van de voorgaande klassen bij elkaar opgeteld
Relatieve cumulatieve frequentie: bij de laatste klassen beginnen met 100% en dan terug
tellen.
8.3 oppervlakten onder de normaalkromme
De notatie normalcdf (l, r ,μ ,σ).
In deze afbeelding is de notatie
(-10^99, 18, 15, 3).
Afspraak: rond oppervlakten onder
normaalkrommen af op 3 decimalen.
Grenzen berekenen met de GR.
Als de oppervlakte gegeven is i.p.v. de grenzen, dan kun je met invNorm uitrekenen wat
de grenzen zijn. De notatie hierbij is (opp., μ ,σ).
Is de oppervlakte onder de normaalkromme
van links van a gegeven, dan is
a=invNorm(opp links, μ ,σ)
Als je de oppervlakte van rechts van a wilt
berekenen, dan moet je de uitkomst van
links van a van een aftrekken.
Afspraak: bij het uitrekenen van a=invNorm(opp links, μ ,σ) moet je op een decimaal meer
afronden dan de gegeven σ.
Het berekenen van de μ en σ.
Met de formule
kun je de μ en σ uitrekenen.
1. GRAPH y1
, y2opp. linkse gebied
2. V-window goed instellen
3. G-solv  ISCT
4. de x die je uitkrijgt door ISCT is de gevraagde μ of σ.
Dus:
Oppervlakte: normNCD
Grens: inverseNorm
Standaardafwijking of gemiddelde:
8.4 toepassingen van de normale verdeling
Percentages en kansen bij de normale verdeling.
Stappenplan voor opgaven over de normale verdeling:
1. Schets de normaalkromme en verwerk hierin l, r ,μ ,σ en opp..
2. Kleur het gebied dat bij de vraag hoort.
3. Bereken met de GR het ontbrekende getal.
4. Beantwoord de gestelde vraag.
Hoeveel is de oppervlakte van het gebied onder de normaalkromme links van
168?=hoeveel procent van de mannen is kleiner dan 168 cm?=wat is de kans dat een
willekeurig gekozen man van deze groep kleiner is dan 168 cm?