2 - iziit

Appendix 1 Isometrie
1.1 Isometrie
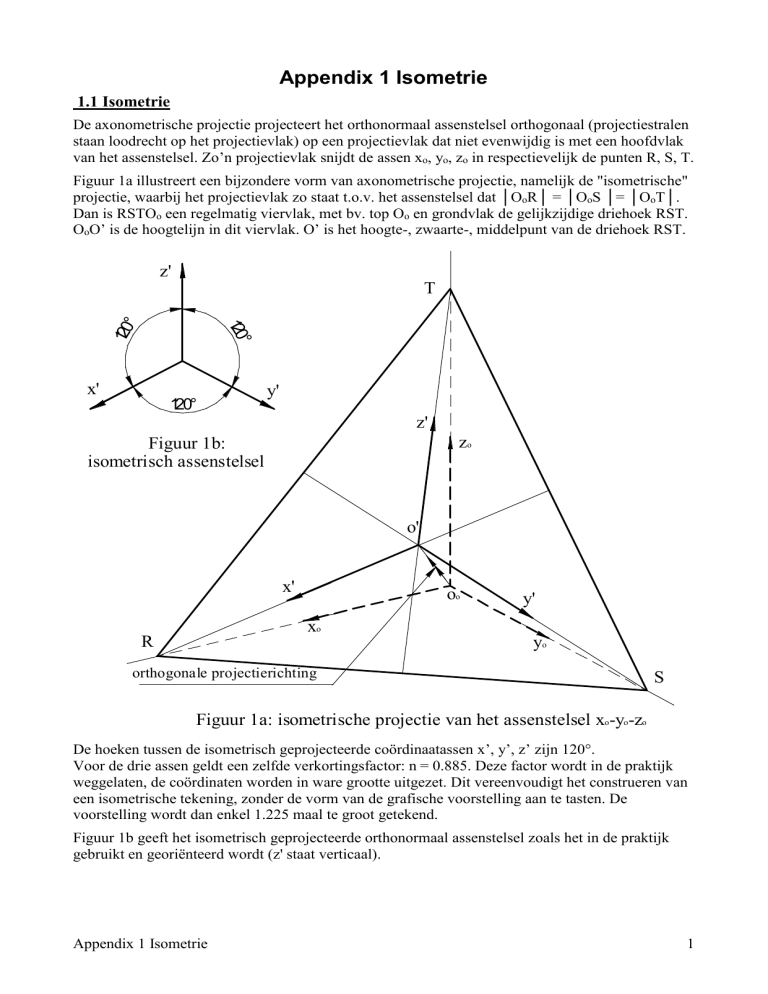
De axonometrische projectie projecteert het orthonormaal assenstelsel orthogonaal (projectiestralen
staan loodrecht op het projectievlak) op een projectievlak dat niet evenwijdig is met een hoofdvlak
van het assenstelsel. Zo’n projectievlak snijdt de assen xo, yo, zo in respectievelijk de punten R, S, T.
Figuur 1a illustreert een bijzondere vorm van axonometrische projectie, namelijk de "isometrische"
projectie, waarbij het projectievlak zo staat t.o.v. het assenstelsel dat │OoR│ = │OoS │= │OoT│.
Dan is RSTOo een regelmatig viervlak, met bv. top Oo en grondvlak de gelijkzijdige driehoek RST.
OoO’ is de hoogtelijn in dit viervlak. O’ is het hoogte-, zwaarte-, middelpunt van de driehoek RST.
z'
°
120
120
°
T
x'
120°
y'
z'
zo
Figuur 1b:
isometrisch assenstelsel
o'
x'
oo
y'
xo
R
yo
orthogonale projectierichting
S
Figuur 1a: isometrische projectie van het assenstelsel xo-yo-zo
De hoeken tussen de isometrisch geprojecteerde coördinaatassen x’, y’, z’ zijn 120°.
Voor de drie assen geldt een zelfde verkortingsfactor: n = 0.885. Deze factor wordt in de praktijk
weggelaten, de coördinaten worden in ware grootte uitgezet. Dit vereenvoudigt het construeren van
een isometrische tekening, zonder de vorm van de grafische voorstelling aan te tasten. De
voorstelling wordt dan enkel 1.225 maal te groot getekend.
Figuur 1b geeft het isometrisch geprojecteerde orthonormaal assenstelsel zoals het in de praktijk
gebruikt en georiënteerd wordt (z' staat verticaal).
Appendix 1 Isometrie
1
1.2 De isometrische projectie van een cirkel
De isometrische projectie van een cirkel gelegen in een vlak evenwijdig met een hoofdvlak van het
orthonormaal assenstelsel wordt een ellips. Figuur 2 illustreert het construeren van zo’n ellips.
Z'
Ø
x
1
Y
A
y
x
2
X'
1'
D'
D
A'
Y'
B
2'
4'
4
C
3
Ø
X
B'
C'
3'
y
grote as 2'4' = 1.225 x Ø
kleine as 1'3' = 0.707 x Ø
Figuur 2 : Isometrische projectie van een cirkel.
Een cirkel met diameter Ø ligt bijvoorbeeld in het xy-vlak of in een vlak er mee evenwijdig.







Zet de coördinaten (x,y) van het centrum van de cirkel uit in het isometrisch assenstelsel.
De cirkel kan ingeschreven worden in een vierkant waarvan de zijden evenwijdig zijn met
de x-as en de y-as. We gebruiken acht punten om de ellips te tekenen. Vier van deze
punten zijn de middens van de zijden van het vierkant, de punten A, B, C en D. De vier
andere punten zijn de snijpunten van de cirkel en de diagonalen van het vierkant, de
punten 1, 2, 3 en 4. We tekenen eerst de isometrische projectie van het omgeschreven
vierkant.
De isometrische projectie van het omgeschreven vierkant bepalen we door eerst de
middellijnen A’C’ en B’D’ te tekenen en dan de zijden. Het resultaat is een ruit.
De cirkel raakt aan het omgeschreven vierkant in de punten A, B, C, D. De ellips raakt aan
de omgeschreven ruit in de punten A’, B’, C’, D’.
De diagonalen van het vierkant worden in isometrische projectie een lange diagonaal en
een korte diagonaal van de ruit. De verlengings-, respectievelijk verkortingsfactor voor
deze diagonalen zijn: 1.225 en 0.707. De punten 1, 2, 3, 4 zijn snijpunten van de cirkel en
de diagonalen van het vierkant en ze liggen op een afstand Ø/2 van het centrum van het
vierkant. Hun isometrische projecties liggen op de diagonalen van de ruit op een afstand
van het centrum van de ruit die 0.707 x Ø/2 is voor de korte diagonaal en 1.225 x Ø/2
voor de lange diagonaal.
Met deze gegevens kunnen acht punten van de geprojecteerde cirkel bepaald worden.
Bovendien is in elk van deze acht punten de richting van de raaklijn gekend.
Deze acht punten en de bijbehorende raaklijnen volstaan om de isometrische projectie van
de cirkel te tekenen.
Appendix 1 Isometrie
2
Tip voor het tekenen van congruente ellipsen
Z
In de isometrische projectie van de nevenstaande
omwentelingscilinder zijn de cirkels in het bovenvlak en het
ondervlak van de cilinder, ellipsen geworden. De twee ellipsen
zijn congruent. De omwentelingsas van de cilinder ligt op de z-as.
X
Y
De acht punten waarmee de ellips van het bovenvlak wordt
geconstrueerd, kan je verplaatsen evenwijdig met de
omwentelingsas over een afstand H, de hoogte van de cilinder.
Zo verkrijg je de acht punten voor de ellips van het ondervlak.
Van deze ellips wordt enkel het zichtbare deel voorgesteld.
1.3 De snijlijn van twee vlakken
Figuur 3 toont een balk die afgeschuind is. Het schuine vlak ABCD heeft de helft van het bovenvlak
van de balk weggenomen en driekwart van het voorvlak van de balk.
Er is ook een gleuf gefreesd. De gleuf ligt centraal. De diepte van de gleuf is een kwart van de
hoogte van de balk, de breedte van de gleuf is de helft van de breedte van de balk.
De ribbe RQ kan je volgens twee methoden construeren.
Methode 1
Van het bodemvlakje PQRS van de gleuf kunnen de ribbe PS en de rechten t en u waarop de ribben
PQ en SR liggen getekend worden via de afmetingen van de gleuf.
De ribbe QR is de snijding van het bodemvlakje PQRS en het schuine vlak ABCD van de balk.
Deze ribbe ligt op de snijlijn v van het vlak vl(P,Q,R,S) en het vlak vl(A,B,C,D).
De rechthoek WXYZ is de snijding van vl(P,Q,R,S) en de balk.
De punten E en F zijn dan twee punten van vl(P,Q,R,S) en vl(A,B,C,D), dus van hun snijlijn v.
Het punt Q is dan het snijpunt van t en v. Analoog voor R.
Methode 2
Van het zijvlakje NOPQ van de gleuf kunnen de ribben OP en ON en de rechte t getekend worden
via de afmetingen van de gleuf.
De evenwijdige vlakken vl(N,O,P) en vl(C,D,Z) worden gesneden door vl(A,B,C). De snijlijnen
zijn dus evenwijdig: de ribbe NQ is evenwijdig met DC. Zo vinden we Q op t.
t
O
W
N
P
u
D
F
Q
Z
S
X
A
R
v
C
E
Y
B
Figuur 3 De snijlijn van twee vlakken
Appendix 1 Isometrie
3