Toepassingen op matrices - Opgave

Toepassingen op matrices - Opgave
Toepassing 1. Matrices en aantal verbindingen in grafen
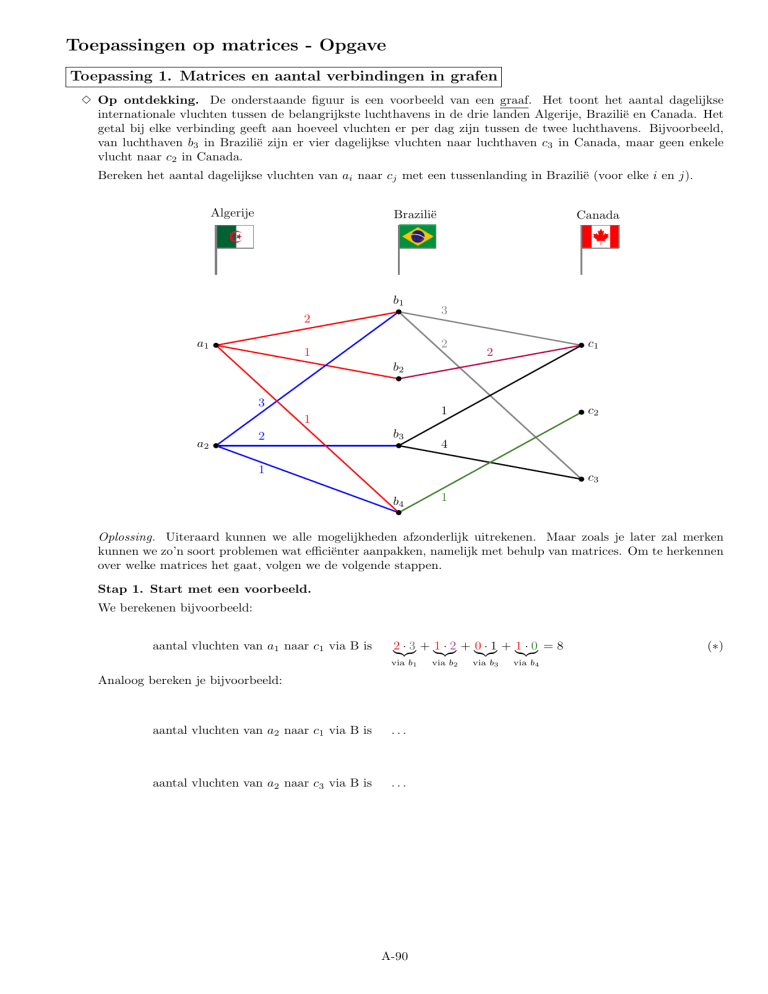
3 Op ontdekking. De onderstaande figuur is een voorbeeld van een graaf. Het toont het aantal dagelijkse
internationale vluchten tussen de belangrijkste luchthavens in de drie landen Algerije, Brazilië en Canada. Het
getal bij elke verbinding geeft aan hoeveel vluchten er per dag zijn tussen de twee luchthavens. Bijvoorbeeld,
van luchthaven b3 in Brazilië zijn er vier dagelijkse vluchten naar luchthaven c3 in Canada, maar geen enkele
vlucht naar c2 in Canada.
Bereken het aantal dagelijkse vluchten van ai naar cj met een tussenlanding in Brazilië (voor elke i en j).
Algerije
Brazilië
b1
2
a1
Canada
3
2
1
c1
2
b2
3
a2
2
c2
1
1
b3
4
1
c3
b4
1
Oplossing. Uiteraard kunnen we alle mogelijkheden afzonderlijk uitrekenen. Maar zoals je later zal merken
kunnen we zo’n soort problemen wat efficiënter aanpakken, namelijk met behulp van matrices. Om te herkennen
over welke matrices het gaat, volgen we de volgende stappen.
Stap 1. Start met een voorbeeld.
We berekenen bijvoorbeeld:
aantal vluchten van a1 naar c1 via B is
2 · 3 + |{z}
1 · 2 + |{z}
0 · 1 + |{z}
1·0 =8
|{z}
via b1
Analoog bereken je bijvoorbeeld:
aantal vluchten van a2 naar c1 via B is
...
aantal vluchten van a2 naar c3 via B is
...
A-90
via b2
via b3
via b4
(∗)
Stap 2. Herken in Stap 1 een vermenigvuldiging van matrices.
In de bewerking (∗) herkennen we:
aantal vluchten van a1 naar c1 via B is
2 1
Analoog herken je:
...
aantal vluchten van a2 naar c1 via B is
...
...
aantal vluchten van a2 naar c3 via B is
 
3
2 
0 1 ·
1 = 8
0
...
...
 
...
. . .

... · 
. . . = . . .
...
...
 
...
. . .

... · 
. . . = . . .
...
Stap 3. Voeg alle rijen in een matrix P , en alle kolommen in een matrix Q.
Om met één bewerking het aantal dagelijkse vluchten van ai naar cj via Brazilië te berekenen, maken we volgende
matrixvermenigvuldiging:


3 0 2
2 1 0 1 
2 0 0
 = ...
·
3 0 2 1 1 0 4
|
{z
} 0 1 0
P
|
{z
}
Q
Zo is bijvoorbeeld het aantal vluchten van a2 naar c3 met een tussenlanding in Brazilië gelijk aan het (. . . , . . .)-de
element van de matrix P · Q, en dat is gelijk aan . . .
Opmerking. De matrix P stelt het aantal directe verbindingen van Algerije naar Brazilië voor, ook wel de
directe-wegenmatrix (of éénstapsverbindingsmatrix) van Algerije naar Brazilië genoemd.
%
a1
a2
b1
b2
b3
b4
2
1
1
0
0
2
1
1
2 1
matrix P =
1 0
0 1
2 1
Pik = aantal directe wegen van ai naar bk
De notatie ‘a1 % b1 ’ wijst op het aantal wegen van a1 naar b1 , namelijk a1 % b1 = 2.
Analoog stelt matrix Q de directe wegenmatrix van Brazilië naar Canada voor.
%
b1
b2
b3
b4
c1
c2
c3
3
2
1
0
0
0
0
1
2
0
4
0

3
2
matrix Q = 
1
0
0
0
0
1

2
0

4
0
A-91
Qkj = aantal directe wegen van bk naar cj
3 Modelvoorbeeld De volgende graaf toont het aantal metroverbindingen tussen vier stations s1 , s2 , s3 en s4 .
(a) Bereken met behulp van matrices het aantal verbindingen van si naar sj
met één tussenstop in een willekeurige station (voor elke i en j).
(b) Wat is het aantal verbindingen van s2 naar s3 met één tussenstop? Lees
dit af uit je antwoord op (a).
Metro van Londen
(c) Bereken met behulp van matrices het aantal verbindingen van s4 naar
s1 met twee tussenstops in willekeurige stations. Maak gebruik van je
grafische rekenmachine.
(d) Bereken met behulp van matrices het aantal verbindingen van s1 naar s1 met tien tussenstops in willekeurige
stations. Maak gebruik van je grafische rekenmachine.
s2
s1
s4
s3
Oplossing.
(a) Om te herkennen over welke matrices het gaat, volgen we terug ons stappenplan.
Stap 1. Start met een voorbeeld.
We berekenen bijvoorbeeld:
aantal verbindingen van s1 naar s4
via één tussenstop is
· . .}. + .|. .{z
· . .}. + .|. .{z
· . .}. = . . .
.|. .{z
· . .}. + .|. .{z
via s1
via s2
via s3
(∗∗)
via s4
Stap 2. Herken in Stap 1 een vermenigvuldiging van matrices.
In de bewerking (∗∗) herkennen we:
 
...
. . .
aantal verbindingen van s1 naar s4

... ... ... ... · 
. . . = . . .
via één tussenstop is
...
Stap 3. Voeg alle rijen in een matrix P , en alle kolommen in een matrix Q.
Om met één bewerking het aantal verbindingen van si naar sj via één tussenstop te berekenen, maken we
volgende matrixvermenigvuldiging:

 

... ... ... ...
... ... ... ...
. . . . . . . . . . . . . . . . . . . . . . . .

 

. . . . . . . . . . . . · . . . . . . . . . . . . = . . .
... ... ... ...
... ... ... ...
|
{z
} |
{z
}
P
Q
Opmerking. In dit voorbeeld is de matrix Q gelijk aan de matrix P . Dat komt omdat het beginstation, de tussenstop en het eindstation nu eender welk station mag zijn. Daarom noemt men P de
directe-wegenmatrix (of éénstapsverbindingsmatrix) van de totale graaf.
(b) Het aantal verbindingen van s2 naar s3 met één tussenstop gelijk aan het (. . . , . . .)-de element van de matrix
P 2 , en dat is gelijk aan . . .
A-92
(c) Hoe kunnen we met één bewerking het aantal verbindingen van station si naar sj met twee tussenstops
berekenen?
Het berekenen kan met behulp van de grafische rekenmachine.
2ND
MATRIX
EDIT
2ND
MATRIX
ENTER
1:[A]
4
ENTER etc.
∧ . . . ENTER
2ND
QUIT
>
Zo is het aantal wegen van s4 naar s1 met twee tussenstops gelijk aan het (. . . , . . .)-de element van de
matrix . . .
en dus gelijk aan . . .
Opmerking. De matrix . . .
noemen we de . . . stapsverbindingsmatrix van de totale graaf.
(d) Hoe kunnen we met één bewerking het aantal verbindingen van station si naar sj met tien tussenstops
berekenen?
Het berekenen kan met behulp van de grafische rekenmachine.
Zo is het aantal wegen van s1 naar s1 met tien tussenstops gelijk aan het (. . . , . . .)-de element van de
matrix . . .
en dus gelijk aan . . .
Opmerking. De matrix . . .
noemen we de . . . stapsverbindingsmatrix van de totale graaf.
A-93
Toepassing 2. Matrices en migratie- en populatievoorspellingen
3 Op ontdekking We beschouwen een eenvoudig model voor de verandering
van het aantal inwoners in een bepaalde stad t.o.v. het platteland.
Onderstel dat ieder jaar 5% van de inwoners van de stad verhuizen naar het
platteland en dat ieder jaar 3% van de inwoners van het platteland verhuizen
naar de stad. Stel in 2012 wonen er 60000 mensen in de stad en 40000 mensen
op het platteland.
(a) Bepaal het aantal inwoners in de stad en op het platteland na twee jaar en
na vijf jaar. Maak gebruik van je grafische rekenmachine.
Jan Van Eyckplein,Brugge
(b) Naar welke waarde evolueert het aantal mensen in de stad? Maak gebruik van je grafische rekenmachine.
Oplossing. We kunnen de migratiebeweging voorstellen met behulp van de volgende graaf:
0, 05
0, 97
0, 95
platteland
stad
0, 03
Ook hier kunnen we het probleem wat efficiënter aanpakken met behulp van matrices. Om te herkennen over
welke matrices het gaat, volgen we de volgende stappen.
Stap 1. Start met een voorbeeld.
We berekenen bijvoorbeeld:
aantal mensen in de stad
na één jaar:
Analoog bereken je bijvoorbeeld:
aantal mensen op platteland
na één jaar:
0, 95 · 60000
|
{z
}
0, 03 · 40000
{z
}
|
+
aandeel van stad
= 58200
(∗)
aandeel van platteland
...
Stap 2. Herken in Stap 1 een vermenigvuldiging van matrices.
In de bewerking (∗) herkennen we:
aantal mensen in de stad
na één jaar:
Analoog herken je:
aantal mensen op platteland
na één jaar:
60000
0, 03 ·
= 58200
40000
0, 95
...
... ·
...
...
= ...
Stap 3. Voeg alle rijen in een matrix P , en alle kolommen in een matrix Q.
Om met één bewerking het aantal mensen in de stad en op het platteland na één jaar te berekenen, maken we
volgende matrixvermenigvuldiging:
60000
0, 95 0, 03
·
= ...
40000
0, 05 0, 97
{z
} | {z }
|
P
Q
Opmerking. De matrix P stelt de (procentuele) bijdragen voor die een plaats (stad of platteland) genereert voor
een andere plaats (stad of platteland), ook wel een overgangsmatrix 1 (of migratiematrix) genoemd.
.
stad
platteland
stad
platteland
0, 95
0, 05
0, 03
0, 97
0, 95 0, 03
matrix P =
0, 05 0, 97
Pij = proc. aandeel van plaats j naar i
De notatie ‘stad . platteland’ wijst op het procentueel aandeel bij overgang van platteland naar stad, namelijk
stad . platteland = 0, 05.
1 Een
overgangsmatrix is een vierkante matrix waarvoor de som van elke kolom gelijk is aan 100%.
A-94
(a) Hoe kunnen we met één bewerking het aantal inwoners in de stad en op het platteland na twee jaar
berekenen? En na vijf jaar?
(b) Hoe kunnen we nagaan naar welke waarde het aantal mensen in de stad evolueert?
A-95
3 Modelvoorbeeld De bioloog K. Evers bestudeert een insectensoort. Hij beschikt over 3000 eitjes, 2000 larven en 1000 insecten. Elke levensfase (ei, larve
en insect) duurt één maand. Hij plaatst de eitjes, larven en insecten in een
afgesloten ruimte. Na één maand is de situatie als volgt:
. Van de eitjes is 95% opgegeten of niet uitgekomen. De rest is uitgekomen.
. Van de larven heeft 20% zich ontwikkeld tot insect. De rest is dood.
. Van de oorspronkelijke insecten is er niet één meer over. Maar ze hebben
elk gemiddeld 100 eitjes voortgebracht.
(a) Stel de populatiebeweging voor met behulp van een graaf.
(b) Bepaal met behulp van matrices het aantal eitjes, larven en insecten na
één maand, twee maanden en acht maanden.
(c) Naar welke waarde evolueert het aantal eitjes? Maak gebruik van je grafische rekenmachine.
Roodkopvuurkever
(Pyrochroa serraticornis)
Oplossing.
(a) We kunnen de overgang van de levensfasen voorstellen met volgende graaf:
100
eitje
0, 05
larve
insect
0, 2
(b-c) Om te herkennen over welke matrices het gaat, volgen we terug ons stappenplan.
Stap 1. Start met een voorbeeld.
We berekenen bijvoorbeeld:
aantal eitjes
na één maand:
.|. .{z
· . .}.
+
aandeel van eitjes
.|. .{z
· . .}.
aandeel van larven
+
.|. .{z
· . .}.
= ...
(∗∗)
aandeel van insecten
Stap 2. Herken in Stap 1 een vermenigvuldiging van matrices.
In de bewerking (∗∗) herkennen we:


...
aantal eitjes
...
... ... ... ·  ...  =
na één maand:
...
Stap 3. Voeg alle rijen in een matrix P , en alle kolommen in een matrix Q.
Om met één berekening de populatie (eitjes, larven en insecten) na één maand te kennen maken we de
volgende matrixvermenigvuldiging:

 

... ... ...
...
. . . . . . . . . ·  . . .  = . . .
... ... ...
...
|
{z
} | {z }
P
Q
Opmerking. De matrix P stelt de fracties voor die een levensfase genereert voor een andere levensfase, ook
wel een Leslie-matrix 2 (of populatievoorspellingsmatrix) genoemd.
2 Een
Leslie-matrix is een vierkante matrix P waarvan enkel de elementen op de eerste rij en de elementen vlak onder de diagonaal mogen
verschillen van het getal 0. Het model van Leslie werd beschreven door P.H. Leslie 1945 [16], en vereist een populatie die niet onderhevig
is aan migratie en waarbij slechts één sexe, meestal de vrouwelijke, wordt beschouwd.
A-96
(b) Hoe kunnen we met één bewerking het aantal eitjes, larven en insecten na twee maanden berekenen? En
na acht maanden?
(c) Hoe kunnen we nagaan naar welke waarde het aantal eitjes, larven en insecten streeft?
A-97