Uploaded by
common.user3097
Genereren van een spanning in een spoel

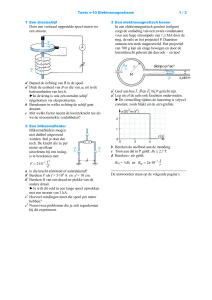
Genereren van een spanning in een spoel Bekijk even onderstaand filmpje ▪ Ik moet eerlijk toegeven dat het filmpje een beetje saai lijkt, maar al de wetten en regels rond elektromagnetisme worden hierin nog even duidelijk herhaald. Probeer zelf mee actief te denken tijdens het filmpje, dan wordt het plots een stuk interessanter. ▪ Klaar? ▪ Elektromagnetische inductie, 5V -YouTube Inductiestroom ▪ Vorige les hebben we geleerd hoe de inductiespanning juist ontstaat. Je weet wel, de lorentzkracht (die door fluxverandering ontstaat) zal de elektronen die rond de atomen zweven naar de ene kant duwen waardoor er (in onderstaand voorbeeld) onderaan de geleider een hoop negatieve atomen en bovenaan een hoop positieve atomen komen staan. Er staat dus een ladingsverschil op de geleider. Als we dan een gesloten stroomkring aansluiten op die geleider willen de atomen weer neutraal zijn waardoor de elektronen onderaan de staaf via de gesloten stroomkring, door onze verbruiker, naar de positief geladen atomen gaan. Er ontstaat dus een stroom. Deze stroom wordt inductiestroom genoemd. Inductiespanning in een spoel ▪ Vorige les hebben we gepraat over een rechte geleider in een veranderend magnetisch veld. (fluxverandering) ▪ We hebben ook gezien dat het geen verschil uitmaakt of we de geleider bewegen in het magnetisch veld, of het veld bewegen rond de geleider. Beiden geven hetzelfde resultaat. (fluxverandering, lorentzkracht, ladingsverschil dus inductiespanning) ▪ Vandaag gaan we kijken wat er nu gebeurt in een spoel. Spoel • Een spoel bestaat uit een rechte geleider die rond een kern gedraaid werd. • Het stukje draad dat 1x rond de kern gedraaid zit noemen we een winding. • De kern versterkt de magnetische werking van de spoel maar wordt ook vaak verwijderd. Wel of geen spoel hangt af van de functie van de spoel. winding Kern Waarom een spoel en geen rechte geleider? ▪ De welgekende formule E = B . l . v vertelt ons dat de opgewekte inductiespanning “E” afhangt van onder andere de lengte “l” van de geleider die zich in de fluxverandering bevindt. ▪ Deze lengte kunnen we vergroten door de rechte geleider op te winden tot een spoel. x aantal windingen Werkbare Werkbare lengte lengte Nog even dit: Wet van Lenz ▪ We hebben van horen zeggen dat de wet van Lenz beweert dat de opgewekte emk “E” de oorzaak van zijn ontstaan zal tegenwerken. ▪ Laat ons dat eens even gaan bekijken. Magneet beweegt niet Geen stroom Magneet draait met de klok, positieve stroom Magneet draait tegen de klok, negatieve stroom Galvanometer wijst de stroomzin aan S N I • • • • • • • • • De galvanometer wijkt uit naar rechts. De stroom zal dus rechtsom lopen. Onderaan de spoel zal de stroom in ons blad gaan. Om bovenaan de spoel weer uit het bad te komen. De rechterhandregel of de kurkentrekker tonen ons de zin van het magnetisch veld rond de geleider. Boven de spoel tegen de klok. Onder de spoel met de klok mee. Binnen de spoel gaan alle veldlijnen dus van links naar rechts. Rechts verlaten de veldlijnen de spoel, dit is dus de N van de spoel. Links zit dan de Z. Wet van Lenz. • De wet van Lenz zal de oorzaak van zijn ontstaan tegenwerken. • Uit de vorige slide bleek dat de N – pool van de spoel rechts stond. • Dit is tegengesteld aan de magneet. • De lorentzkracht zal de oorzaak van zijn ontstaat, het bewegen van de magneet, dus gaan tegenwerken. bewegingszin S N Handboek ▪ Neem je handboek vanaf p.117. ▪ We overlopen samen even de antwoorden. Er wordt geen stroom opgewekt. wijkt in beide zinnen lichtjes uit lichtjes tegengewerkt tijdens de beweging De galvanometer wijkt in beide zinnen sterk uit. Naarmate je sneller beweegt is de uitwijking groter maw, de opgewekte stroom is groter Deze gaat in de omgekeerde zin van het uitwijkingspatroon uitwijken. Idem als beginsituatie De sterkere magneet wekt een grotere stroom op. De spoel met 1500 windingen wekt meer stroom op stroom opgewekt gegenereerd inductie tegengewerkt zin zin aantal windingen snelheid sterkte veldlijnen aansnijdt Het bepalen van de zin van de opgewekte emk “E” Regel: • Bepaal de zin van het elektromagnetisch veld van de spoel met de Wet van Lenz. • Bepaal de zin van de inductiestroom met de rechterhandregel in de spoel. • De spoel kan nu beschouwd worden als een bron. Bepaal de polariteit van deze bron over de weerstand R en de geïnduceerde stroomzin door de weerstand. Bepaal de zin van het elektromagnetisch veld van de spoel met de Wet van Lenz. ▪ De wet van Lenz vertelt ons dat de inductiespanning zo gericht is dat ze de oorzaak van haar ontstaan zal tegenwerken. ▪ Aangezien de magneet met zijn Z-pool richting de spoel beweegt mogen er dus van uitgaan dat de inductiespanning in die zin zal zijn dat ze een Z pool aan de rechterkant zal creëren. ▪ Links krijgen we dus de N-pool van de spoel. N Z Bepaal de zin van de inductiestroom met de rechterhandregel in de spoel. ▪ We weten dat de veldlijnen binnen in de magneet van Z naar N gaan. ▪ Hierdoor weten we dat de magnetische velden van de geleiders bovenaan kloksgewijs zullen draaien en onderaan tegen de klok. ▪ Als we de rechterhandregel of de kurkenrekkerregel gaan toepassen zien we dat de stroom bovenaan in ons blad gaat ▪ En onderaan uit ons blad komt. Bepaal de polariteit over de weerstand R en de geïnduceerde stroomzin door de weerstand. ▪ Onderaan komt de stroom uit ons blad en dus ook uit de spoel. ▪ De stroom gaat rechts in onze weerstand en komt er links weer uit ▪ Om nadien bovenaan de spoel weer in de spoel te gaan. De grootte van de opgewekte emk “E” ▪ Hoe meer windingen “N” in het (veranderend) magnetisch veld, hoe sterker de opgewekte E. N≈E ▪ Flux duiden we aan met symbool Ф Verandering duiden we aan met wiskundig symbool ∆ Fluxverandering wordt dus aangeduid als ∆ Ф ▪ Wanneer we een magneet stil houden in of naast de spoel zal er in de spoel geen fluxverandering plaatsvinden en dus ook geen E worden opgewekt. Hoe groter de fluxverandering , hoe groter de opgewekte E ∆ Ф ≈E ▪ Ook de snelheid waarmee we de magneet of de spoel bewegen heeft invloed op de opgewekte E. Hoe sneller de beweging, hoe meer ∆ Ф per tijdseenheid “t” deze factor duiden we aan met symbool ∆ t De grootte van de opgewekte emk “E” ▪ De fluxverandering per tijdseenheid “∆ t” moeten we even beter bekijken. Hoe sneller we de magneet of spoel bewegen, hoe sneller de fluxverandering “∆ Ф”. Als de fluxverandering plaats vindt op 4s wordt een bepaalde E opgewekt. Als de fluxverandering sneller plaatsvindt, bv op 2s, wordt een grotere E opgewekt. ▪ Hoe kleiner de tijdspanne “∆ t” hoe groter de opgewekte E ▪ ∆ t is dus omgekeerd evenredig met E Wiskundig schrijven we dan: 1 ≈E ∆t Formule ▪ Als we vorige bevindingen samen gieten krijgen we volgende formule. ▪ E=N . ∆Ф ∆t Oefeningen p 121 en 122 ▪ Los de volgende oefeningen op in je cursus op p. 121 en 122. ▪ Trek er nadien een foto van en zet ze in de uploadzone. ▪ Op de volgende dia krijg je alvast de eerste oefening cadeau. Oefening 1 p.121 Einde Succes!