Uitwerkingen - Noordhoff Uitgevers

■■
7
Kracht en beweging
■■
Introductie
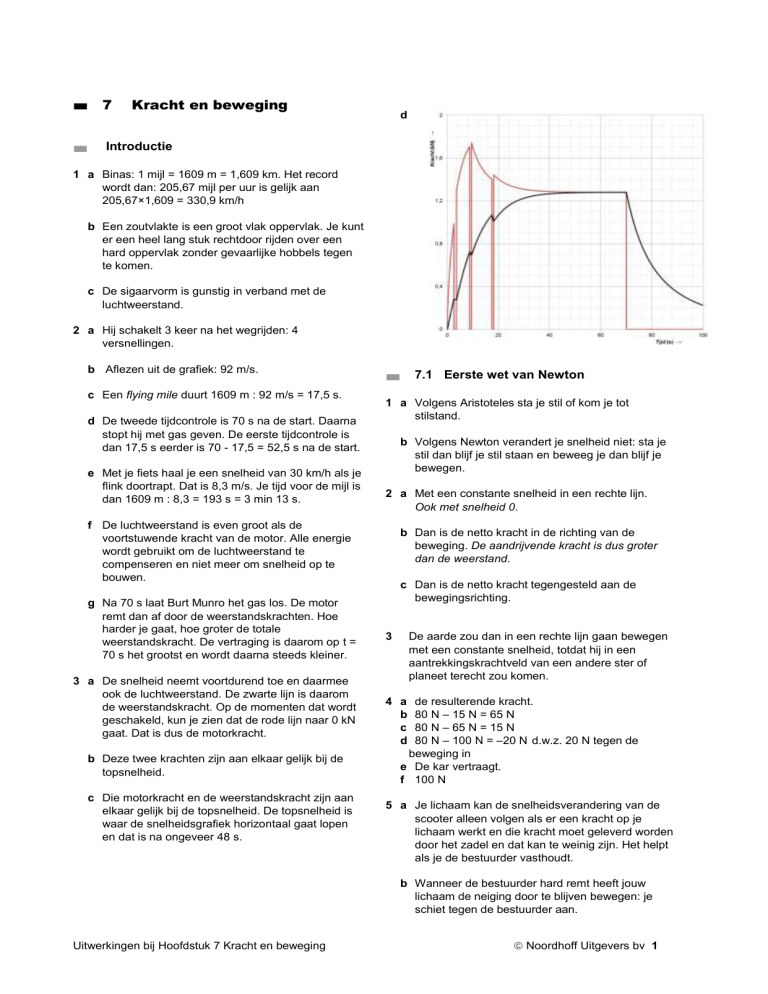
d
1 a Binas: 1 mijl = 1609 m = 1,609 km. Het record
wordt dan: 205,67 mijl per uur is gelijk aan
205,67×1,609 = 330,9 km/h
b Een zoutvlakte is een groot vlak oppervlak. Je kunt
er een heel lang stuk rechtdoor rijden over een
hard oppervlak zonder gevaarlijke hobbels tegen
te komen.
c De sigaarvorm is gunstig in verband met de
luchtweerstand.
2 a Hij schakelt 3 keer na het wegrijden: 4
versnellingen.
b Aflezen uit de grafiek: 92 m/s.
c Een flying mile duurt 1609 m : 92 m/s = 17,5 s.
d De tweede tijdcontrole is 70 s na de start. Daarna
stopt hij met gas geven. De eerste tijdcontrole is
dan 17,5 s eerder is 70 - 17,5 = 52,5 s na de start.
e Met je fiets haal je een snelheid van 30 km/h als je
flink doortrapt. Dat is 8,3 m/s. Je tijd voor de mijl is
dan 1609 m : 8,3 = 193 s = 3 min 13 s.
■■
1 a Volgens Aristoteles sta je stil of kom je tot
stilstand.
b Volgens Newton verandert je snelheid niet: sta je
stil dan blijf je stil staan en beweeg je dan blijf je
bewegen.
2 a Met een constante snelheid in een rechte lijn.
Ook met snelheid 0.
f De luchtweerstand is even groot als de
voortstuwende kracht van de motor. Alle energie
wordt gebruikt om de luchtweerstand te
compenseren en niet meer om snelheid op te
bouwen.
g Na 70 s laat Burt Munro het gas los. De motor
remt dan af door de weerstandskrachten. Hoe
harder je gaat, hoe groter de totale
weerstandskracht. De vertraging is daarom op t =
70 s het grootst en wordt daarna steeds kleiner.
3 a De snelheid neemt voortdurend toe en daarmee
ook de luchtweerstand. De zwarte lijn is daarom
de weerstandskracht. Op de momenten dat wordt
geschakeld, kun je zien dat de rode lijn naar 0 kN
gaat. Dat is dus de motorkracht.
b Deze twee krachten zijn aan elkaar gelijk bij de
topsnelheid.
c Die motorkracht en de weerstandskracht zijn aan
elkaar gelijk bij de topsnelheid. De topsnelheid is
waar de snelheidsgrafiek horizontaal gaat lopen
en dat is na ongeveer 48 s.
7.1 Eerste wet van Newton
b Dan is de netto kracht in de richting van de
beweging. De aandrijvende kracht is dus groter
dan de weerstand.
c Dan is de netto kracht tegengesteld aan de
bewegingsrichting.
3
De aarde zou dan in een rechte lijn gaan bewegen
met een constante snelheid, totdat hij in een
aantrekkingskrachtveld van een andere ster of
planeet terecht zou komen.
4 a
b
c
d
de resulterende kracht.
80 N – 15 N = 65 N
80 N – 65 N = 15 N
80 N – 100 N = –20 N d.w.z. 20 N tegen de
beweging in
e De kar vertraagt.
f 100 N
5 a Je lichaam kan de snelheidsverandering van de
scooter alleen volgen als er een kracht op je
lichaam werkt en die kracht moet geleverd worden
door het zadel en dat kan te weinig zijn. Het helpt
als je de bestuurder vasthoudt.
b Wanneer de bestuurder hard remt heeft jouw
lichaam de neiging door te blijven bewegen: je
schiet tegen de bestuurder aan.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 1
12
a/b
6 a Doordat de rolweerstand erg klein is zal de kar als
hij eenmaal beweegt door willen gaan met die
beweging. Je hoeft dus alleen de rolweerstand te
overwinnen en die is klein.
b
b Als hij stilstaat en je wilt hem in beweging
brengen.
c Als je hem af wilt remmen en als je de bocht om
wilt.
a
d Bij een volle kar, die is moeilijker in beweging te
krijgen en moeilijker af te remmen.
7
De schaatsen van een vallende schaatser hebben
geen grip meer op het ijs. De glijweerstand op het
ijs is erg klein en dus zal de schaatser de
beweging blijven volgen die hij op dat moment
heeft. Dat is rechtdoor en dus volgt hij de bocht
niet.
8 a Langzaam of lui. Bijvoorbeeld een slak of een
bepaald type leerling.
b Als het voorwerp een grote massa heeft.
Dan duurt het lang om de snelheid te veranderen.
9
Het binnenste van een rauw ei is vloeibaar. Zo’n
vloeistof draait als je het ei een tijdje rondgedraaid
heeft mee. Als je het ei plotseling tot stilstand
brengt, draait de vloeistof nog een tijdje door. Die
vloeistof neemt vervolgens het ei weer mee als je
het loslaat. De traagheid van de vloeistof zorgt er
dus voor dat het ei weer gaat draaien.
10 a Rolweerstand en luchtweerstand.
b 15 N.
Je snelheid is constant. De netto kracht is dus
0 N. De totale weerstand moet dus even groot zijn
als de aandrijvende kracht.
c 15 N.
Fnetto = Faandrijvend – Fluchtweerstand =
30 – 15 = 15 N. De weerstand is nog niet
veranderd als je dezelfde snelheid hebt als eerst.
d Als je sneller gaat rijden neemt de luchtweerstand
toe. Na een tijdje is dus de totale weerstand weer
net zo groot geworden als de aandrijvende kracht.
Je gaat dan met een grotere maar weer constante
snelheid vooruit.
13 a Een supertanker is erg zwaar. Zware voorwerpen
hebben een grote traagheid.
b Als je een bocht om wilt moet de tanker reageren
op een zijwaartse kracht. Zo’n zware tanker
reageert traag en wil dus rechtdoor. En als hij
eenmaal draait, stopt hij ook niet zomaar.
c Omdat het bij zo’n zware tanker lang duurt om zijn
snelheid te verminderen.
14 a Wanneer de voorwerpen niet te licht zijn is het
mogelijk om het kleed er onder vandaan te
trekken. Je maakt dan gebruik van de traagheid
van de voorwerpen.
b
Zie de filmpjes: na een aantal mislukte pogingen
lukt het ze (maar dan gaat er weer iets anders
mis...)
15 a De weerstand met het water.
b De weerstand tussen de boot en het onderstel is
veel kleiner. De boot verliest dus niet veel vaart en
schiet door.
c Als je zo’n onderstel gebruikt kun je ervoor zorgen
dat hij erg hard van de helling afglijdt en kun je er
ook voor zorgen dat je boot een eindje boven het
water vooruit schiet, dus nog niet afremt op het
water zelf.
d Antwoord B. Op dat moment is de verandering van
snelheid (en richting) het grootst en hebben de
deelnemers de neiging door de traagheid van hun
lichamen, voorover te klappen.
e Ja, je rijdt harder.
11
Pulsje
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 2
■■
7.2 Kracht en versnelling
wordt twee keer zo groot. De versnelling wordt dus
twee keer zo klein.
16 a Dat hoeft niet. Als de versnelling maar kort duurt
dan is de snelheid niet zo groot.
b Nee de sprinkhaan is niet zwaar. De kracht hoeft
dan niet groot te zijn.
17 a Die heeft de kortste tijd (6,5 s) nodig om van 0 tot
100 km/h te versnellen.
b Hij heeft een grotere motorinhoud en (dus) een
groter vermogen.
c De Daihatsu heeft weliswaar een kleinere
motorinhoud en (dus) een kleiner vermogen, maar
hij is ook veel lichter. Daardoor kan hij toch sneller
optrekken dan de Citroen.
18 a 1 cm3 = 0,001 dm3 = 0,001 L.
De inhoud is dan 3197 x 0,001 = 3,197 L.
b 1 pk = 7,355∙102 W.
Het vermogen is dan 90 x 7,355∙102 = 66 kW
19
kracht (N)
versnelling
(m/s2)
20 a a 
Joris
50
20
Carmen
30
12
Aischa
45
18
William
40
16
v
t
b Een negatieve versnelling betekent dat de
snelheid afneemt: een vertraging
21 a De snelheid na 50 s bereken je met
v  at  0,0027  50  0,135 m/s
b De gemiddelde snelheid van een vliegtuig dat
begint met een snelheid van 0 m/s en eindigt met
een snelheid van 0,135 m/s is de helft van die
eindsnelheid: 0,0675 m/s. De afgelegde afstand is:
𝑠 = 𝑣𝑔𝑒𝑚 ∙ 𝑡 = 0,0675 ∙ 50 = 3,375 = 3,4 𝑚
c De gemiddelde snelheid is 4,2 m : 60 s = 0,07 m/s.
De snelheid op het eind, na 60 s is twee maal het
gemiddelde: 2 × 0,07 = 0,14 m/s. De versnelling is
de snelheidsverandering per seconde: 0,014 : 60
= 0,0023 m/s2.
22 a mtotaal = 55 kg + 15 kg + 70 kg = 140 kg
b De kracht die je uit kunt oefenen op je pedalen
verandert niet. Die is als je fietst met iemand
achterop even groot als zonder die persoon.
Toen je alleen fietste was de versnelling a =
3,0 m/s2 en de massa m = 70 kg.
Daaruit volgt: F = m  a = 3,0  70 = 210 N
Met iemand achterop blijft de trapkracht F =
210 N, m = 140 kg
F 210

 1,5 m/s2.
Dus: a 
m 140
Een snellere en ook juiste redenering is: Je massa
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
23 a 0,50 g =
0,50
 0,00050 kg.
1000
De versnelling van het propje is a 
v
12


t 0,15
80 m/s2.
Hiervoor is een kracht nodig van
F  m  a  0,000 50  80  0,04 N.
b De kracht van het elastiekje is vlak na het loslaten
het grootst, omdat het elastiekje dan het meest is
uitgerekt. De kracht van het elastiekje wordt
daarna steeds kleiner.
24 a De snelheidsafname is 0,165 m/s in 10 s. De
vertraging is: 0,165 : 10 = 0,0165 = 0,017 m/s2.
b De vertraging wordt enkel veroorzaakt door de
rolweerstand:
Frol = ma = 190000 × 0,0165 = 3135 N = 3,1 kN.
c Bereken eerst de versnelling in het eerste deel van
de grafiek. Dan de netto trekkracht. De trekkracht
van Kevin is dan 3135 N groter omdat ook de
rolweerstand gecompenseerd moet worden.
De snelheidstoename is 0,165 m/s in 60 s =
0,00275 m/s2. De netto trekkracht is 190 000 ×
0,00275 = 522,5 N. De trekkracht van Kevin is
522,5 + 3135 = 3657,5 N = 3,7 kN.
F
. De massa moet in kg.
m
Dus wordt het m = 250 g = 0,25 kg.
10
a
 40 m/s2.
0,25
v
b a
Dus v  a  t . Hieruit volgt dan:
t
v  40  0,20  8,0 m/s. Omdat je begint met een
snelheid van 0 m/s, is dat ook de eindsnelheid.
25 a Je gebruikt a 
c 5,0 N. De versnelling wordt twee keer zo klein bij
dezelfde massa. Dan is de benodigde kracht ook
twee keer zo klein.
F
10

 67 m/s2.
m 0,15
26 a 180 N is de stuwkracht. De netto kracht valt af te
leiden uit de versnelling.
Fnetto  m  a  125  1,2  1,5  102 N.
d a
b 3  10 N. Omdat er maar 1,5  102 N van de
1,80  102 N stuwkracht over is moet er een
tegenwerkende kracht zijn van 0,3  102 N. Dat is
de weerstand.
F
F
F
stuw
weerstand zodat
Of formeler: netto
Fweers tan d  Fnetto  Fstuw  150  180 
-3  10 N.
De - betekent dat de weerstand tegenwerkt.
c Als de snelheid groter wordt neemt de
luchtweerstand ook toe.
 Noordhoff Uitgevers bv 3
d Fnetto is nu 180 – 80 = 100 N. De versnelling is
F 100

 0,80 m/s2.
m 125
e Als de scooter op topsnelheid rijdt, verandert zijn
snelheid niet. Er is dan geen netto kracht meer.
f Vlak voor Erik begon te remmen was zijn totale
weerstand 180 N. De totale weerstand als hij
begint te remmen is dus 180 + 500 = 680 N.
F 680


De vertraging die hij krijgt is dus: a 
m 125
5,44 m/s2.
dan a 
De vertraging wordt natuurlijk direct minder omdat
bij afnemende snelheid ook de weerstand kleiner
wordt.
27 a Om de versnelling te berekenen moet je de
nettokracht delen door de massa:
𝐹
12,5
𝑎 = 𝑛𝑒𝑡𝑡𝑜 =
= 0,50 m/s2.
𝑚
b Na 4 s is de snelheid 4 × 0,50 = 2,0 m/s
c De spankracht in het touw is gelijk aan de kracht
die nodig is voor de versnelling plus de kracht die
nodig is om de weerstand van de sneeuw te
compenseren: Fspan = 12,5 + 7,5 = 20 N.
d De nettokracht is nu nul en de trekkracht is gelijk
aan de spankracht en die is gelijk aan de
weerstand van de sneeuw = 7,5 N.
e De vertraging wordt veroorzaakt door de
weerstand van de sneeuw:
𝐹
7,5
𝑎 = 𝑛𝑒𝑡𝑡𝑜 = − = −0,30 m/s2.
25
Elke seconde gaat er 0,30 m/s van de snelheid af.
De slee staat stil na 2,0 : 0,30 = 6,7 s.
f
c F  m  a  10 000  9,8  103 = 9,8  107 N.
d Nee want die kan maar een versnelling van
98,1 m/s2 overleven.
Op het lichaam van een mens van 70 kg zou dan
een kracht komen te staan van 70  9,8  103 =
6,9  105 N. Het gewicht van 70 personenauto’s
op elkaar.
30 a De nettokracht op de motorfiets is 1,4 – 1,06 =
0,34 kN = 340 N.
𝐹
340
𝑎 = 𝑛𝑒𝑡𝑡𝑜 =
= 1,1 𝑚/𝑠 2
2,5
𝑚
2
snelheid in m/s
v 11,2  10 3


t
1,14
b
9,8  103 m/s2.
Als de tijd 100 × korter is, en de
snelheidsverandering hetzelfde, is de versnelling
100 × groter dan in bron 9.
a
(20+5)
𝑚
f De vertraging in het laatste deel is 18 m/s : 5 =
3,6 m/s2. De nettokracht om een passagier met
een massa van 570 : 9,81 = 58,1 kg een
vertraging te geven van 3,6 m/s2 is F = m  a =
58,1  3,6 = 209 N. De kracht van de lift op de
passagier werkt omhoog en de zwaartekracht op
de passagier werkt omlaag. Samen moet dat een
kracht van 209 N omlaag geven omdat de
passagier afremt: Fz - Flift = 209 N en daaruit volgt
Flift = Fz - 209 = 570 - 209 = 361 N. De kracht van
de passagier op de liftvloer (=gewicht) is dan ook
361 N en de passagier is door het afremmen van
de lift lichter geworden.
s
6400
t


s  v gem  t
v gem 11,2  10 3 2
29 a
dus:
1,14 s
Je kunt ook zeggen: de loop is 100 × korter dus de
tijd is 100 × korter dan in bron 9.
300
b Op t = 60 s is de voortstuwende kracht van de
motor gelijk aan de weerstandskracht en de
nettokracht is dan 0 N. De versnelling van de
motormotor is dan ook 0 en de snelheid van Burt
blijft dus constant.
1,5
1
0,5
0
0
2
4
6
8
10
12
14
16
tijs in s
28 a De maximale snelheid is 18,0 m/s is 18.0 × 3,6 =
64,8 km/h.
b De snelheidstoename is 18 m/s in 6 s. De
versnelling is: 16 : 6 = 3,0 m/s2.
c De persoon moet een versnelling krijgen van
3,0 m/s2. Daar is een kracht voor nodig van F =
ma = 58  3,0 = 174 N.
d De gemiddelde snelheid tijdens het afremmen is
de helft van de maximale snelheid: 9,0 m/s. Het
afremmen duurt 5 s. De afstand die tijdens het
afremmen wordt afgelegd is dan 5  9,0 = 45 m.
e De passagier voelt zich lichter omdat zijn lichaam
door de traagheid zijn snelheid naar boven ‘wil
behouden’. Hierdoor duwt de liftvloer minder terug.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 4
7.3 Weerstand en beweging
31 a Wanneer je met je voet op een skateboard staat;
wanneer je met je fiets een bocht wilt maken;
wanneer een auto op een helling staat
geparkeerd.
b Wanneer je aan een parachute in de lucht hangt;
wanneer een schansspringer (skispringer) een
nieuw record wil vestigen, wanneer je een dartpijl
wilt gooien.
32 a luchtweerstand
b rolweerstand
c Als de eindsnelheid is bereikt geldt dat de
luchtweerstand gelijk is aan de zwaartekracht. Het
(frontale) oppervlak van het gummetje is veel
kleiner dan dat van de prop watten. Daardoor
moet het gummetje harder gaan om dezelfde
luchtweerstand te krijgen.
39 a 0 N. Op t = 0 heeft de parachutist nog geen
snelheid. Er is dan nog geen luchtweerstand.
b De versnelling bepaal je met een raaklijn. Zie de
raaklijn bij t = 0 (rode stippellijn).
∆𝑣
30−0
𝑎= =
= 10 𝑚/𝑠 2
∆𝑡
33 a Dan hoef je minder hard te trappen
b fietsen met hard opgepompte banden
c Je slipt bij het wegrijden en je remweg wordt
langer
d Gladde banden of een glad wegdek
34 a luchtweerstand
b snelheid van de trein en de vorm van de trein
(frontaal oppervlak).
35
De weerstand tussen band en grind is erg groot.
36
Pulsje
37
Een vrije val is een valbeweging waarbij er geen
weerstandskrachten werken. Je versnelt dan
voortdurend met de valversnelling (g = 9,81 m/s 2).
Parachutespringers hebben altijd te maken met
luchtweerstand. Natuurkundig gezien is het
daarom geen vrije val.
∆𝑡
8,5−0
𝐹𝑛𝑒𝑡𝑡𝑜 = 𝑚 ∙ 𝑎 = 80 ∙ 10 = 125 = 1,3 ∙ 102 𝑁
30
20
10
0
0
38 a
3−0
(Dit klopt ongeveer: de valversnelling is 9,81 m/s 2)
𝐹𝑛𝑒𝑡𝑡𝑜 = 𝑚 ∙ 𝑎 = 80 ∙ 10 = 800 = 8,0 ∙ 102 𝑁
c Zie de raaklijn bij t = 4 (groene streepjeslijn).
∆𝑣
30−16,7
𝑎= =
= 1,56 = 1,6 𝑚/𝑠 2
Snelheid (m/s) →
■■
5
vv
propje papier
t
15
Tijd (s) →
gummetje
b
10
t
d Flucht = 800 – 125 = 675 N
(Wanneer je met g = 9,81 m/s2 rekent: 660 N)
e De luchtweerstand is dan ook 800 N.
f De parachute gaat open op t = 10 s. De afgelegde
weg bepaal je door hokjes tellen:
1 hokje komt overeen met 1 s∙2 m/s = 2 m
Er zijn 103 hokjes, dus s = 103∙2 = 206 m
Je zou ook vgem kunnen schatten:
vgem = 20 m/s. s = 20∙10 = 200 m
g De luchtweerstand is dan nog steeds 800 N.
40 a De nettokracht is 1000 N - 900 N = 100 N
b a  Fnetto  100  0,42 m/s2
m
240
c Elke sec neemt de snelheid toe met 0,42 m/s. Een
snelheid van 1,0 m/s bereiken, duurt: 1,0 : 0,42 =
2,4 s.
d Als de constante snelheid gehaald is, hebben de
rovers alleen nog kracht nodig om de weerstand te
compenseren: de schuifweerstand van 900 N. Dat
is 450 N per persoon.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 5
e
1,2
snelheid in m/s
1
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
6
tijd in s
41 a De nettokracht is de rolweerstand = 200 N
c De auto rolt nog een tijdje door omdat alleen de
rolweerstand van 200 N de auto afremt.
Bovendien is een auto behoorlijk zwaar en dus
traag.
d De vertraging door de rolweerstand is:
F
2
200
a  rol 
 0,2 m/s
m 1000
De snelheid is 3,3 m/s en elke seconde gaat er 0,2
m/s van de snelheid af: remtijd is 3,3 : 0,2 =
16,5 s. In die tijd rolt de auto nog door met een
gemiddelde snelheid van 3,3 : 2 = 1,65 m/s. De
afstand die tijdens het uitlopen is afgelegd: vgem
 remtijd = 1,65  16,5 = 27,2 m.
e Op t = 12,5 s: vanaf dat tijdstip remt de auto
sneller af.
f De rolweerstand is 200 N. De spierkracht van
Maarten is 250 N. De netto kracht is dan 350 +
200 = 450 N.
g De versnelling is te bepalen uit de grafiek:
∆𝑣
0−3
𝒂= =
= −0,462 m/s2. De auto heeft
∆𝑡
19−12,5
volgens de zo doe je dat een massa van 1000 kg.
𝐹𝑛𝑒𝑡𝑡𝑜 = 𝑚 ∙ 𝑎 = 1000 ∙ 0,462 = 462 N
h De getekende raaklijn aan de grafiek tussen t =
11,0 s en t = 12,4 s snijdt de grafiek in de t-as bij t
= 27,4 s. Dit was de lijn geweest als alleen de
rolweerstand de auto had afgeremd. Dus na 27,4
s.
Je kunt het ook berekenen. De vertraging door
enkel de rolweerstand heb je bij vraag d berekend:
0,2 m/s2. De remtijd heb je daar ook berekend: 3,3
: 0,2 = 16,5 s. Het remmen begon op tijdstip t = 11
s. De auto zou hebben stilgestaan op t = 11 + 16,5
= 27,5 s.
42 a Op t = 0 s is er nog geen snelheid. De nettokracht
is dan 60 N. De door de boot geleverde
spankracht is 240 N. De weerstandskracht is dan
240 – 80 = 180 N
b De versnelling is maximaal als de nettokracht
maximaal is. Dat is aan het begin, dus op t = 0 s.
c De snelheid bereikt zijn maximum als de
nettokracht nul is geworden. Dit is na ongeveer 50
s.
d De luchtweerstand
e
75
Kracht (N) →
b De versnelling is 0,30 m/s2 en die versnelling
houden ze 11 s vol (zie bron 11 zo doe je dat). De
snelheid is dan 0,30  11 = 3,3 m/s.
60
45
30
15
0
0
10
20
30
40
50
Tijd (s) →
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 6
7.4 Zwaartekracht en massa
43 a Je hangt een massa van b.v. 1 kg aan de
krachtmeter. De zwaartekracht die je meet als de
krachtmeter stil hangt is getalsmatig even groot als
de versnelling van de zwaartekracht.
Fz  m  g
g  Fz
Dus als m = 1 kg dan is
.
b Je hangt de onbekende massa aan de
krachtmeter en meet de zwaartekracht op de
krachtmeter. Dit is nu het gewicht van de
onbekende massa. De massa bepaal je nu met:
𝐹𝑧
𝑚=
𝑔
44 a gMars = 3,7 m/s2.
F  m  g Mars  0,64  3,7 
b z
2,4 N.
Fz
25
m


g Mars
3,7
c
6,76 kg dus 6,8 kg
45 a Op Jupiter geldt:
Fz  m  g jupiter  m  24,9  1040
m
N en dus:
1040
 41,8
24,9
kg
b Het gewicht op aarde is:
Fz  m  g Aarde  41,8  9,81  410 N
c Op Jupiter is de gravitatieversnelling
24,9
 2,54
9,81
maal groter dan op aarde. De
weegschaal geeft daardoor een waarde aan die
2,54 maal hoger is dan op Aarde. Op aarde geeft
de weegschaal 41,8 kg aan en op Jupiter 41,8
×2,54 = 106 kg.
46 a Op een massa van 120 g werkt een zwaartekracht
F  mg
 0,120  9,81  1,18
aarde
van: z
N.
b De spierkracht is dan het gewicht van de bal plus
de kracht die nodig is voor de versnelling:
∆𝑣
2,4
𝑚
𝑎= =
= 6,86 2
∆𝑡
0,35
𝑠
𝐹𝑛𝑒𝑡𝑡𝑜 = 𝑚 ∙ 𝑎 = 0,12 ∙ 6,86 = 0,82 𝑁
𝐹𝑠𝑝𝑖𝑒𝑟 = Fz + Fnetto = 1,18 + 0,82 = 2,00 N
1
1
c 𝑣𝑔𝑒𝑚 = ∙ 𝑣𝑚𝑎𝑥 = ∙ 2,4 = 1,2 𝑚/𝑠
2
2
𝑠 = 𝑣𝑔𝑒𝑚 ∙ 𝑡 = 1,2 ∙ 0,35 = 0,42 𝑚 = 42 𝑐𝑚
47
C. Deze dichtheid is 1000 x kleiner dan de andere
dichtheden. De andere eenheden zijn aan elkaar
gelijk: 1 g/cm3 = 1 kg/dm3 = 1 kg/L = 1 g/ml.
48 a De straal r = 1,25 cm = 1,25 · 10-2 m
Het volume is dan:
3
4
4
V     r 3     1,25  10 2   8,18  10 6 m3
3
3
b De dichtheid van staal is 7,8·103 kg·m-3
(hiervoor moet je kijken in de tabel met ‘alliages’,
want staal is geen zuivere stof maar een mengsel
van ijzer en o.a. koolstof)
m = ρ · V = 7,8 · 103 × 8,18 · 10-6 = 0,0638 kg
= 64 gram.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
c De dichtheid van aluminium is 2,78·103 kg·m-3.
Dat is 7,8 / 2,78 = 2,8 x zo klein als staal. Voor
een even zware knikker heb je dus 2,8 x meer
aluminum nodig, dus VAl = 2,8 x 8,18 = 23∙10-6 m3
49 a De massa
b Dan moet je uitrekenen op welke massa de
zwaartekracht 0,50 N is:
F
0,50
m Z 

g
9,81 0,051 kg = 51 g.
c Op de maan werkt deze brievenweger ook. Hij is
namelijk gebaseerd op het vergelijken van een
onbekende massa met een bekende.
50 a
4
Snelheid (m/s) →
■■
3
2
1
0
-1
0
1
2
3
4
5
-2
-3
-4
Tijd (s) →
b De gemiddelde snelheid tijdens de beweging
omhoog is 3,5 m / 2,2 s = 1,59 m/s. De
beginsnelheid is het dubbele van de gemiddelde
snelheid omdat de snelheid gelijkmatig afneemt
van maximaal naar nul. De beginsnelheid is dan
3,18 m/s. En dat is ook de snelheid waarmee je
weer op de grond komt.
c De zwaartekrachtversnelling op deze planeet
bereken je als volgt: in 2,2 s verandert de snelheid
van 0 naar 3,18 m/s. De versnelling is dan:
v 3,18
a

 1,4
t
2,2
m/s2 .
d Eén of andere maan van Jupiter.
e Je sprong naar het hoogste punt duurt: 3,18/9,81
= 0,32 s. Je gemiddelde snelheid naar het hoogste
punt is weer 1,59 m/s. De hoogt die je bereikt is
gemiddelde snelheid × tijd = 1,59 × 0,32 = 0,51 m.
51 a Je doet wat water in een maatcilinder en leest het
volume af. Dan laat je het stukje metaal in het
water zakken en leest opnieuw af. Het verschil is
het volume van het stukje metaal.
Natuurlijk moet je zoveel water nemen dat het
voorwerp helemaal onder water komt. Verder
gebruik je een zo smal mogelijke maatcilinder; dat
leest het nauwkeurigst af.
b 47 g = 0,047 kg; 6,5 mL = 0,0065 L
gebruik een verhoudingstabel:
massa (kg)
0,047
7,23
 Noordhoff Uitgevers bv 7
volume (m3)
0,0065
1,0
dus de dichtheid is 7,23 kg/m3
of vul de formule in: m = ρ · V
0,047 = ρ × 0,0065 
ρ = 0,047 : 0,0065 = 7,23 kg/m3
Volgens Binas kan het zink of chroom zijn, maar
stukjes puur chroom kom je niet vaak tegen.
Als de meting niet al te nauwkeurig is komen ook
tin en gietijzer in aanmerking.
c De stukjes zijn even zwaar. Als het stukje sneller
valt dan een ronde kogel moet het een goede
stroomlijn hebben, bijvoorbeeld langwerpig met
een spitse punt.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 8
oppervlak van de rechthoek is 3 × 46 = 138 m. De
totale afstand is dan 161 + 138 = 299 m = 0,30
km.
Toepassing
Opgave 1 Winterpret
1 De zwaartekracht Fz op een zwaar voorwerp is
groter en dus ook de schuifweerstand volgens het
10
van C naar D: de zwaartekracht
in punt D: de zwaartekracht
van D naar C: de zwaartekracht
11
John: 1c
Dave: 2b
 F
F
z
verband: schuif
2 Bij het linkerdeel van de vergelijking is de eenheid,
de eenheid van kracht: N. Het rechterdeel moet
dan ook als eenheid N hebben en dat is al de
eenheid die hoort bij Fz. De constante kan dan
geen eenheid hebben.
Opgave 3 Radiografisch bestuurbare auto
12
3 Bereken eerst de schuifweerstand en dan
daarmee de vertraging. Met de vertraging en de
beginsnelheid bereken je de remtijd en met de
remtijd tenslotte de remweg. De snelheid van 50
km/h is 13,89 m/s.
Fschuif  Fz  0,25  2000  9,81  4905
a
Fschuif
De vertraging:
t
De remtijd:
De remweg:
vbegin
a
m

N.
4905

 2,45
2000
m/s2.
10 m
1s
14
De groene lijn is de luchtweerstand want die moet
toenemen wanneer de snelheid toeneemt.
De rode lijn is de rolweerstand want die is
nauwelijks afhankelijk van de snelheid.
De zwarte lijn is de nettokracht want die neemt af
door de toenemende luchtweerstand.
De paarse lijn is dan de motorkracht.
4 De nettokracht (in de horizontale richting) is enkel
de schuifweerstand Fschuif.
N.
15
10
Snelheid (m/s) →
2
2
Het uitglijden duurt dan:
s
400
s = vgem ∙ t ⇔ t =
=
= 90 s
vgem 4,44
6 vanaf 4,7 m/s
6
4
2
F
74,7
a  netto 
 0,96
m
78
De vertraging:
m/s2
0
0
Om de kracht uit te rekenen heb je de versnelling
nodig. De versnelling is gelijk aan de helling van
de grafiek in de eerste 7 seconde.
a
8
12
16
20
Tijd (s) →
v 46

 6,57 m/s2.
t
7
De afstand is gelijk aan de oppervlakte onder de
grafiek van t = 0 tot t = 10 s. Verdeel het oppervlak
in een driehoek en een rechthoek. Het oppervlak
van de driehoek is: 0,5×7×46 = 161 m. Het
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
4
De versnelling op t = 0 is gelijk aan de helling
(richtingscoëfficiënt) van de raaklijn:
∆v
10
a= =
= 1,82 m/s2
∆t
5,5
De nettokracht is dan
Fnetto = m ∙ a = 2,2 ∗ 1,82 = 4,0 N
De nettokracht die de magneten uitoefenen is dan
F  ma  6200  6,57  4,07  104 N.
9
8
7 De schuifweerstand is 7,7 N en de luchtweerstand
is 67 N. De nettokracht is dan 67 + 7,7 = 74,7 N.
Opgave 2 Tower of Terror
8
36 km
1h
Bepaal de oppervlakte onder de grafiek van t = 0 s
tot t = 6 s. Teken een passende driehoek en de
afgelegde afstand is inderdaad 28 m.
Je kunt ook hokjes tellen (14 hokjes) of eerst de
gemiddelde snelheid schatten (ongeveer 4,7 m/s).
13,89
s  vgemiddeld  t 
 5,67  39
2
m
5 De snelheid waarmee Sven over de finish gaat is
32 km/h = 32 / 3,6 = 8,9 m/s. De gemiddelde
snelheid over het traject van 400 m (1 rondje) is:
v +v
8,9+0
vgem = 1 2 =
= 4,44 m/s
3600 × 10 = 36000
3600 s
13
13,89
 5,67
2,45
s
Fschuif  Fz  0,010  78  9,81  7,6518  7,7
Volgens de grafiek is de maximale snelheid 10 m/s
en dat is inderdaad gelijk aan 36 km/h.
Met een verhoudingstabel:
16
De snelheid is dan nog klein en daardoor ook de
luchtweerstand. Daaruit volgt dat de rolweerstand
gelijk is aan 1,0 N want dan geldt:
Fnetto = Fmotor - Frol.
 Noordhoff Uitgevers bv 9
17
FL  0,040  v 2 . Op t = 6,0 s is de snelheid 8,0 m/s
en de luchtweerstand FL  0,040  8  2,56 N.
De rolweerstand is nog steeds 1,0 N. Fnetto = Fmotor
- Flucht - Frol = 5,0 - 2,56 - 1,0 = 1,44 = 1,4 N
2
18
Bij de maximumsnelheid (10 m/s) moet de
nettokracht 0 N zijn, want is de nettokracht groter
dan 0 N dan gaat de auto nog harder en is de
nettokracht kleiner dan 0 N dan remt de auto. De
luchtweerstand bij 10 m/s is dan volgens de
tweede grafiek: 5,0 N - 1,0 N = 4,0 N. Dat is weer
gelijk aan:
FL  k  v 2 waarbij je moet aantonen dat k =
2
2
0,0040. Dus FL  4,0  k  v  k  10 dus
k
Daarna moet je de versnelling a  v bepalen voor
t
4,0
 0,040
100
de raaklijn, waarbij je de snelheid in km/h ook nog
omrekent naar m/s (delen door 3,6):
a
Opgave 4 Supervogels?
19
-
20
De sprongkracht is nodig om het gewicht van de
vogel te compenseren en voor het versnellen, dus:
sprongkracht = gewicht + m·a
3000 = 150·9,81 + 150×a
150×a = 3000 - 150·9,81 = 1528
a = 1528 / 150 = 10,19 N = 10,2 m/s2.
21
De eindsnelheid: v = a t = 10,2 × 0,700 = 7,14 m/s.
22
Het aantal vleugelslagen per minuut is dan 60 ×
1,2 = 72.
Je weet nu de versnelling, de massa is gegeven
(m =8,1∙103 kg) en met Fres = m∙a kun je nu de
resulterende kracht berekenen. Die is: Fres
=8,1∙103 × 0,80 = 6,5∙103 N. Dit vergelijk je met de
waarde in figuur 3 en dan kun je zien dat dat
overeen stemt.
27
23
11000 kg
1 cm2
11000×10000
10000 cm2
11·107 kg
1 m2
11·107×9,81 N
1 m2
antwoord: 11·108 N/m2 = 1,1·109 N/m2
24
Die kracht is 90 kg/cm2 komt overeen met 883
N/cm2. Een kies met een oppervlakte van 0,60
cm2 geeft dan een kracht van 0,60× 833 = 530 N =
0,53 kN.
Opgave 5 Superbus
25
26
Je moet de optrekafstand aan de hand van de
figuur bepalen. Dus niet met formules rekenen.
Het is een v-t grafiek en de oppervlakte onder de
grafiek is de afgelegde weg. Je kunt de grafiek zo
aanpassen dat het een makkelijk figuur wordt. Als
je hier van een driehoek uitgaat, krijg je basis (105
s) maal halve hoogte (= 0,5 × 250 / 3,6) = 3,7∙103
m.
De bus wordt aangedreven door de Fres. Die zorgt
ervoor dat er de eerste 10 seconden een
constante versnelling is. Die versnelling kun je uit
figuur 2 halen door een raaklijn vanuit het begin te
trekken, zie figuur.
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
v 300 / 3,6

 0,80 m/s2
t
104
.
In de figuur kun je zien dat de motorkracht groter
is dan de resulterende kracht. Het verschil tussen
die twee wordt veroorzaakt door de wrijving. Op
het moment t = 0 s begint de bus te bewegen. Er
is dan nog geen luchtweerstand, want hij beweegt
immers nog niet door de lucht. De enige
weerstand die er dan op dat moment is, is de
rolweerstand: Frol. Deze kracht vermindert het
effect van de motor. De grootte van Fw,rol is gelijk
aan het verschil tussen de motorkracht en de
resulterende kracht: Frol=Fmotor−Fres. Aflezen van
de beide waarden voor Fmotor en Fres levert dan
voor de Frol = 7,8 − 6,5= 1,3 kN = 1,3⋅103 N.
28
Om de luchtwrijvingscoëfficiënt te kunnen
berekenen moet je naast de gegeven waarden ook
de grootte van de luchtweerstand Flucht hebben.
Bij constante snelheid is de nettokracht gelijk aan
nul. De voorwaartse kracht is de kracht van de
motor en de tegenwerkende kracht is de
weerstandskracht, die bestaat uit de rolweerstand
Frol en de luchtweerstand Flucht .
Fw,lucht = Fmotor−Fw,rol = 4,8⋅103 −1,3⋅103 =
3,5⋅103 N.
Door nu de gegevens in te vullen kun je de cw
waarde berekenen:
3,5⋅103 = ½ cw∙1,2×2,50×1,70×(69,4)2
3,5⋅103 = 1,23∙104 ∙cw
cw = 3,5⋅103/1,23∙104 = 0,28
 Noordhoff Uitgevers bv 10
Opgave 5 Vallen op de maan
29
Vallende voorwerpen die geen luchtwrijving
ondervinden, vallen met dezelfde versnelling.
Luchtwrijving wordt veroorzaakt door een
dampkring. Die is kennelijk afwezig, dus Scott
heeft gelijk.
30
𝑣𝑔𝑒𝑚 =
∆𝑠
∆𝑡
1
=
1,5
1,36
= 1,1
𝑚
𝑠
𝑣𝑔𝑒𝑚 = ∙ 𝑣𝑚𝑎𝑥 ⇔ 𝑣𝑚𝑎𝑥 = 2 ∙ 1,1 = 2,2 𝑚/𝑠
2
𝑎=𝑔=
∆𝑣
∆𝑡
=
2,2
1,36
= 1,6 𝑚/𝑠 2
Dit is in overeenstemming met de waarde in Binas.
31
Bij de door ons gekozen oplossingsmethode
hebben we dat bij vraag 30 al gedaan: 2,2 m/s
32
even groot, groter
33
Volgens Binas tabel 6 is de afstand aarde-maan
gelijk aan s = 3,8∙108 m. Volgens tabel 7 is de
lichtsnelheid ongeveer 3,0∙108 m/s. Voor de tijd
geldt dan:
𝑠
3,8∙108
𝑣
3,0∙108
𝑡= =
= 1,3 𝑠
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 11
■■
b gMaan = 1,63 m/s2; m = 75 kg
Fz  m  g  75  1,63  1,2  102 N.
Voorbeeldproefwerk
1 a In een bocht moet de bewegingsrichting
veranderen. Daar is een kracht voor nodig. Als de
aanhanger die kracht niet goed op de betonmolen
over kan brengen gaat het fout. De betonmolen
gaat dan rechtdoor.
b Als je hard remt, of erg snel optrekt. Dan gaat de
betonmolen door met bewegen, of blijft juist achter.
2 a de zwaartekracht en de luchtweerstand
b Direct na het springen is de zwaartekracht groter
dan de luchtweerstand
Als de snelheid constant is zijn beide krachten
even groot.
5
De dichtheid van staal is 7,8 · 103 kg·m-3
massa (kg)
volume (m3)
7,8 · 103
1,0
350
0,0449
Er zit dus 0,0449 m3 staal in de carrosserie. Met
het andere metaal kan dat 40% minder worden,
dan blijft dus 60% over: 0,60 × 0,0449 = 0,0269 m 3
Gemaakt van het lichtere metaal is de massa
hiervan:
m = ρ · V = 4,9 · 103 × 0,0269 = 132 kg
De auto wordt dus 350 – 132 = 218 kg lichter.
c De luchtweerstand, want de parachutist remt dan af.
d De netto kracht is dan 0 N. De snelheid verandert
namelijk niet.
e Die zijn in beide gevallen even groot. Ze zijn net
zo groot als de zwaartekracht en die is niet
veranderd. In beide gevallen gaat de parachutist
met een constante snelheid naar beneden. Dat
kan alleen als de weerstand net zo groot is als de
zwaartekracht.
3 a a
F
2400

 1,8 m/s2
m 1340
b Bereken eerst Fnetto:
Fnetto  m  a  1340  1,6  2,1  103 N. De
aandrijvende kracht is nog steeds 2,4 kN. De
weerstand van de weg is dus 2,4 – 2,1 = 0,3 kN =
3  102 N.
c Ze wordt juist naar voren geduwd. Ze komt iets
minder snel op gang dan de auto. Ze blijft dus een
beetje achter, totdat haar stoeltje haar ‘meeneemt’.
d m
F 25

 16 kg
a 1,6
e v  110  20  90 km/h 
90
 25 m/s
3,6
v 25

 6,3 m/s2.
t
4,0
F  m  a  1340  6,3  8 375 N = 8,4 kN.
a
f Dan zou zijn hoofd door de klap van achter
achterover klappen, waardoor hij nekletsel op zou
kunnen lopen. Zijn hoofd gaat namelijk niet vanzelf
naar voren als de auto van achter een harde duw
krijgt. Zijn hoofd kantelt door de kracht waarmee
zijn nek eraan trekt, als er geen hoofdsteun is. Die
kracht veroorzaakt het nekletsel.
4 a tot 10 N
Uitwerkingen bij Hoofdstuk 7 Kracht en beweging
 Noordhoff Uitgevers bv 12