Naam onderdeel

Nu voor straks NaSk 1 deel 4 KGT leerboek
Hoofdstuk 13 Constructies 1
Hoofdstuk 13: Constructies
13.1 Wat weet je er nog van?
1
B
2
a
Fz
3
b
2 cm komt overeen met 8 N, dus 1 cm komt overeen met 4 N.
a
3,0 cm x 15 N/cm = 45 N
b
500 N komt overeen met 2,5 cm, dus 1 cm komt overeen met
500 N
= 200 N.
2,5
13.2 Soorten krachten
4
even groot als.
5
Als je een kabel oprolt, wil je geen duwkrachten hebben.
6
a
b
Een balk (als tafelpoot) kan het tafelblad ophoog houden, een touw kan dit niet.
Voorbeelden zijn scheerlijnen van een tent, de schoten van een zeilboot en het touw van een
vlieger.
13.3 Krachten samenstellen
7
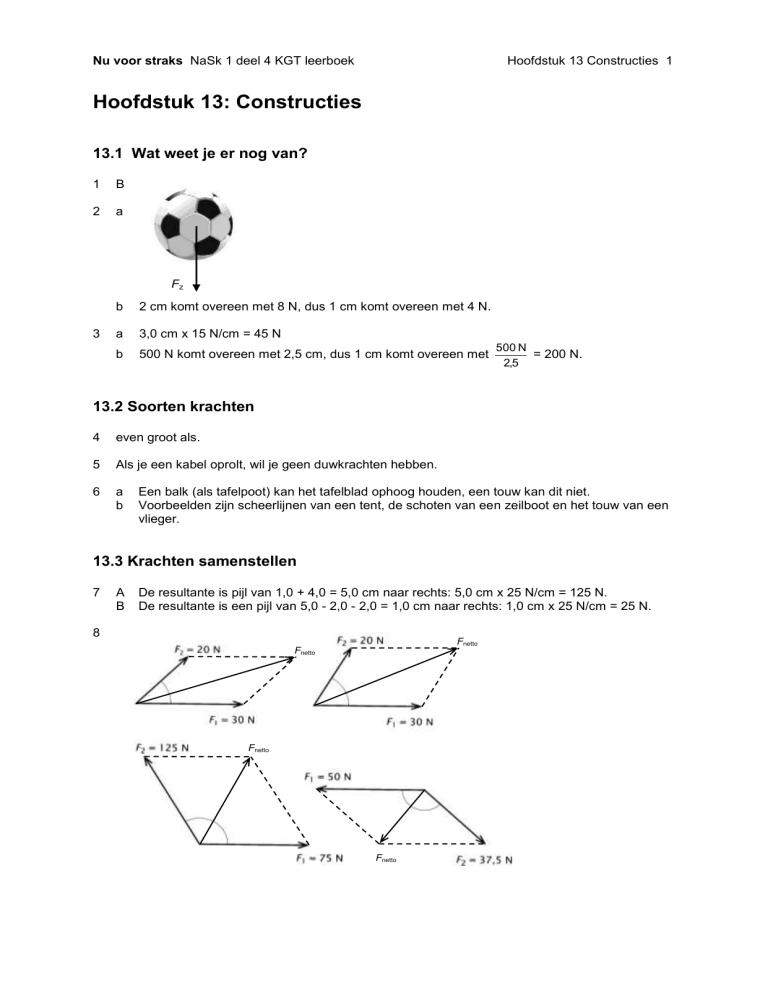
A
B
De resultante is pijl van 1,0 + 4,0 = 5,0 cm naar rechts: 5,0 cm x 25 N/cm = 125 N.
De resultante is een pijl van 5,0 - 2,0 - 2,0 = 1,0 cm naar rechts: 1,0 cm x 25 N/cm = 25 N.
8
Fnetto
Fnetto
Fnetto
Fnetto
Nu voor straks NaSk 1 deel 4 KGT leerboek
9
Hoofdstuk 13 Constructies 2
In de tekening komt 1 cm overeen met 2000 N.
Fnetto is 5,1 cm lang. Dit komt overeen met een kracht
van 5,1 cm x 2000 N/cm = 10 200 N.
Fnetto
Fstuw = 10 000 N
Fwater =
2000 N
veerpont
13.4 Een kracht ontbinden
10 krachten optellen of krachten samenstellen.
11 a
b
Fspan
Fspan
Linker tekening: 1,7 cm x 2 000 N/cm = 3 400 N per koord.
Rechter tekening: 3,0 cm x 2 000 N/cm = 6 000 N per koord.
Die spankracht moet de zwaartekracht opheffen en is recht omhoog gericht, dus 6 000 N.
Nu voor straks NaSk 1 deel 4 KGT leerboek
Hoofdstuk 13 Constructies 3
13.5 Moment en massamiddelpunt
12 Omdat de arm van een lange moersleutel groot is, kun je met dezelfde kracht een groter moment
uitoefenen op de moer.
13 Dan is de arm van de spierkracht groter en kan hij makkelijker voorkomen dat de halter gaat
kantelen.
14 a
b
De arm van de kracht om de kruiwagen op te tillen is 5,0 x zo groot als de arm van de
zwaartekracht (100 cm in plaats van 20 cm). De kracht die je moet leveren is dus ook 5,0 x zo
klein als de zwaartekracht:
c
15 a
b
1 000 N
= 200 N.
5,0
Er is evenwicht. De reactiekracht van de grond en de kracht bij het handvat (200 N) heffen
samen de zwaartekracht (1 000 N) op. De reactiekracht is dus 1 000 N - 200 N = 800 N.
De arm is twee maal zo groot, dus de kracht is twee maal zo klein: 300 N.
Deze kracht moet de andere krachten opheffen: 600 N + 300 N = 900 N
16 Midden in de balk (lengte 15 cm, breedte 2,5 cm en hoogt 2 cm)
17 a
b
Omdat het ventiel zwaarder is dan de rest van de bal draait het ventiel naar onder.
Nee, het ligt blijkbaar meer aan de kant van het ventiel.
18 a
De zwaartekracht Fz = m x g = 50 kg x 10 N/kg = 500 N. Er is evenwicht, dus het
linksdraaiend moment is gelijk aan het rechtsdraaiend moment.
De afstand tot het draaipunt van Ffreek is 2 x zo groot als de afstand van de zwaartekracht tot
het draaipunt. De kracht van Freek is dus ½ x 500 N = 250 N.
Er is evenwicht. De reactiekracht van de grond en de spierkracht van Freek heffen samen de
zwaartekracht op. De reactiekracht is 500 N - 250 N = 250 N.
Dan zal de balk verder omhoog komen.
b
c
Nu voor straks NaSk 1 deel 4 KGT leerboek
Hoofdstuk 13 Constructies 4
13.6 Krachten in de praktijk
19 De pijlen die de kracht op het koord weergeven in de tekening op blz 130 zijn 3,0 cm lang.
Deze kracht is dus 3,0 cm x 2 N/cm = 6,0 N.
20 a
Fg
b
c
De pijl die deze kracht weergeeft, is 2,1 cm lang. De kracht is 2,1 cm x 2 N/cm = 4,2 N.
Ja, als het koord langer is, wordt de kracht op de draad kleiner (4,2 N i.p.v. 6,0 N).
21 De kabels houden elkaar in evenwicht. De twee kabels aan de rechterkant moeten in evenwicht
zijn met tientallen kabels aan de linkerkant. De kracht op elk van beide rechter kabels is veel
groter dan de kracht op elk van de linkerkabels. Daarom zijn de beide rechterkabels dikker.
22 In veel kasten is aan de achterkant en in veel bedden aan de onderkant een diagonale balk
bevestigd. Deze maakt een driehoek om de kast of het bed in de juiste vorm te houden.
23 De vrachtwagen oefent een kracht uit van Fz = m x g =
10 000 kg x 10 N/kg = 100 000 N.
In de tekening wordt een krachtenschaal gebruikt van 2,5 cm per
100 000. Dit is 40 000 N per cm.
De extra spankracht is een aangegeven met een pijl van 3,0 cm.
Dit komt overeen met een toename van de spankracht in de kabel
met 3,0 cm x 40 000 N/cm = 120 000 N.
24 a
b
25 a
b
Vakwerk bestaat uit driehoeken. Driehoeken zijn stevig van
vorm.
De kracht van het dak die de muren naar buiten duwt, wordt
met een horizontale balk opgevangen.
De verticale balken houden het dak omhoog.
De horizontale balken zorgen dat het dak de muren niet naar
buiten drukt.
De diagonale balken vormen driehoeken. Dit geeft de
constructie extra stevigheid.
In de muur zitten dikke verticale balken. Deze ondersteunen
de randen van het dak. Als je zo'n balk weghaalt, moet je het dak daar stutten.
26 De component langs de helling is het deel van de
zwaartekracht dat meewerkt of tegenwerkt bij het fietsen op de
helling.
27 De krachtenschaal is 8 kN per 2,7 cm, dat is 3,0 kN per cm.
De component langs de helling is 0,9 cm. Dat is een kracht van
0,9 cm x 3,0 kN/cm = 2,7 kN.
Nu voor straks NaSk 1 deel 4 KGT leerboek
Hoofdstuk 13 Constructies 5
13.7 Afsluitende vragen
28 a
b
29 C
30
De pijl die de nettokracht weergeeft is 5,1 cm. Dit komt overeen met 5,1 cm x 25 N/cm = 128 N.
31
100 N komt overeen met 2,5 cm. De krachtenschaal is 40 N/cm.
De nettokracht is 2,1 cm. Dit komt overeen met 2,1 cm x 40 N/cm = 84 N
32 Zie ook het antwoord bij vraag 20. In situatie 2 is de hoek tussen de draad en de richting van de
zwaartekracht kleiner. Hierdoor wordt de kracht op de draad ook kleiner.
33 a
b
c
De zwaartekracht F = m x g = 250 kg × 10 N/kg = 2 500 N,
De arm l = 4,0 m – 1,5 m = 2,5 m.
Het moment M = F x l = 2 500 N x 2,5 m = 6 250 Nm linksdraaiend.
Je hebt een rechtsdraaiend moment van 6 250 Nm nodig om de slagboom te openen.
Dan verschuift het zwaartepunt van de slagboom naar links en is er een kleiner moment nodig
om de slagboom te laten draaien.
Het rechtsdraaiend moment moet gelijk zijn aan het linksdraaiend moment: 6250 Nm.
Het contragewicht zit op 0,75 m van het draaipunt.
De zwaartekracht van het contragewicht is dus F = M/l =
De massa is
8 333 N
= 833 kg.
10
6250 Nm
= 8 333 N.
0,75 m
Nu voor straks NaSk 1 deel 4 KGT leerboek
34 a
Fwind
Hoofdstuk 13 Constructies 6
Fstuw
Froer
b
c
1 cm komt overeen met 200 N
De pijl van de stuwkracht is 2,15 cm lang. Dit is 2,15 cm x 200 N/cm = 430 N.
De kracht van het roer moet de zijwind tegengaan (zie tekening). Deze pijl is 1,25 cm lang. Dit
is een kracht van 1,25 cm x 200 N/cm = 250 N.
35 a
b
36 a
De resultante van F2 en F3 is een pijl van 3,7 cm. F1 is een pijl met een lengte van 2,6 cm.
De nettokracht is dus een pijl met een lengte van 3,7 cm - 2,6 cm = 1,1 cm.
Dit komt overeen met een nettokracht van 1,1 cm x 50 N/cm = 55 N naar rechtsonder.
Om de resultante van F2 en F3 op te heffen, moet F1 een pijl zijn met een lengte van 3,7 cm.
Dit is een kracht van 3,7 cm x 50 N/cm = 185 N.
Op de auto werkt een zwaartekracht Fz = m x g = 1 100 kg x 10 N/kg = 11 000 N.
De achterwielen werken als draaipunt.
Het rechtsdraaiend moment Mrechts = Fz x lrechts = 11 000 N x 1,2 m = 13 200 Nm.
Het linksdraaiend moment en het rechtsdraaiend moment zijn gelijk bij evenwicht.
M links = F links x l links = F links x 3,0 m = 13 200 Nm .
F links =
13 200 Nm
= 4 400 N.
3,0 m
b
c
37 a
De krachten zijn recht omhoog en recht omlaag gericht. De kracht dwars op de hijsarm is 0 N.
De massa van de brug zorgt voor een linksdraaiend moment.
Fz = m x a = 500 kg x 10 N/kg = 5 000 N .
Deze kracht grijpt aan in het midden van de brug op 2 m van het draaipunt.
M links = F links x l links = 5 000 N x 2 m = 10 000 Nm.
Het contragewicht zorgt voor een rechtsdraaiend moment.
Fz = m x a = 1600 kg x 10 N/kg = 16 000 N
Deze kracht grijpt aan op 1 m in het midden van de brug op 2 m van het draaipunt.
M rechts = F lrechts x l rechts = 16 000 N x 1 m = 16 000 Nm.
Nu voor straks NaSk 1 deel 4 KGT leerboek
b
c
d
e
38 a
b
c
Hoofdstuk 13 Constructies 7
groter
[De vraag in het leerboek is helaas niet juist, correctie volgt in nieuwe oplage].
[De vraag in het leerboek is helaas niet juist, correctie volgt in nieuwe oplage].
Het contragewicht zorgt ervoor dat het ophalen van de brug gemakkelijker wordt zodat
iemand de brug in zijn eentje kan ophalen.
Op het stuk AC werken trekkrachten, op het stuk BC duwkrachten.
De zwaartekracht van 250 N wordt weergegeven door een pijl van 2,0 cm. Dit is 125 N per
cm. De pijl die de spankracht aangeeft is 2,8 cm lang. Dit komt overeen met een kracht van
2,8 cm x 125 N/cm = 350 N.
De horizontale component van de spankracht in het doek zorgt voor een kracht op de muur in
punt B. De pijl die deze component weergeeft is 2,0 cm lang. Dit komt overeen met een
kracht van 2,0 cm x 125 N/cm = 250 N.