Junior Wiskunde Olympiade 2012-2013: eerste ronde

Junior Wiskunde Olympiade 2012-2013: eerste ronde
1. Hoeveel is
p√
(A) 3
4+
√
9+
√
16?
(B) 29
(C)
√
29
(D)
√
3
29
(E)
C
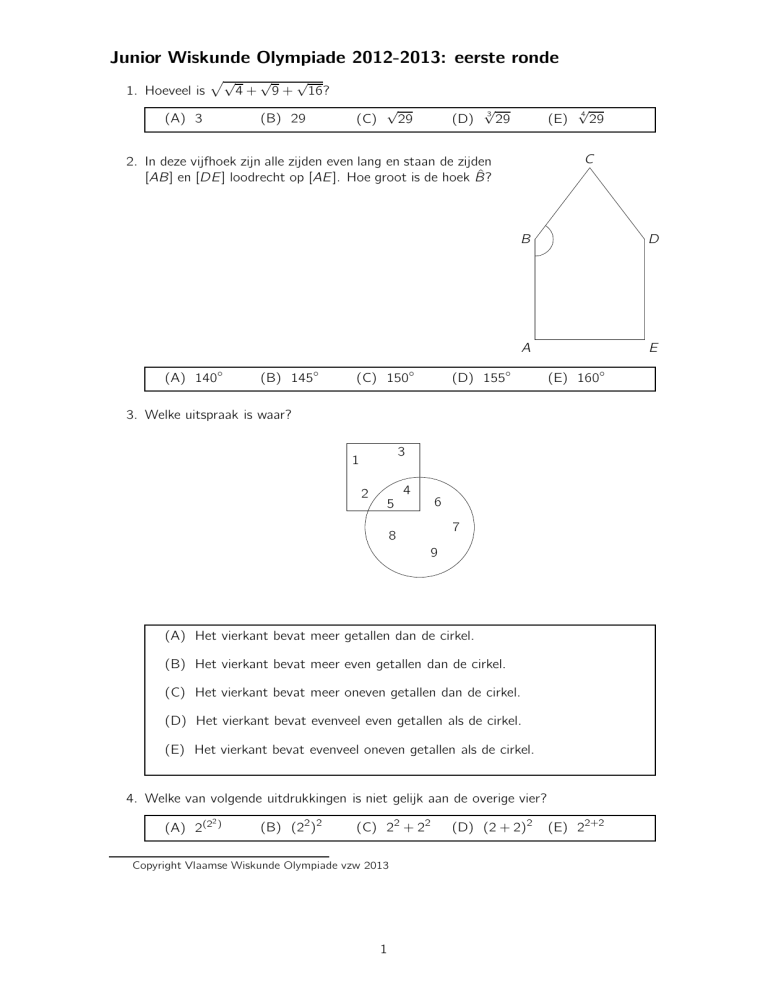
2. In deze vijfhoek zijn alle zijden even lang en staan de zijden
[AB] en [DE] loodrecht op [AE]. Hoe groot is de hoek B̂?
(A) 140◦
(B) 145◦
(C) 150◦
√
4
29
B
D
A
E
(D) 155◦
(E) 160◦
3. Welke uitspraak is waar?
3
1
2
4
6
5
7
8
9
(A) Het vierkant bevat meer getallen dan de cirkel.
(B) Het vierkant bevat meer even getallen dan de cirkel.
(C) Het vierkant bevat meer oneven getallen dan de cirkel.
(D) Het vierkant bevat evenveel even getallen als de cirkel.
(E) Het vierkant bevat evenveel oneven getallen als de cirkel.
4. Welke van volgende uitdrukkingen is niet gelijk aan de overige vier?
2)
(A) 2(2
(B) (22 )2
(C) 22 + 22
Copyright Vlaamse Wiskunde Olympiade vzw 2013
1
(D) (2 + 2)2
(E) 22+2
5. Welk getal moet je op de stippellijn invullen opdat er in het vierkant een ware uitspraak
zou staan?
11111
In dit vierkant
staat . . . keer
het cijfer 1.
11111
(A) 10
(D) 13
(B) 11
(E) 11 111 111 111
(C) 12
6. Wat is het derde cijfer na de komma van de oplossing van de vergelijking 27x − 6 = 0?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
7. Het getal 24X8Y bestaat uit vijf cijfers. Het getal is deelbaar door 9 en door 10. Wat
is de som van de cijfers X en Y ?
(A) 4
(B) 5
(C) 9
(D) 10
(E) 13
8. Een rooster met 13 × 13 vakjes wordt opgevuld zoals in de figuur.
3
1
4
2
5
3
1
4
2
5
3
1
4
4
2
5
3
1
4
2
5
3
1
4
2
5
5
3
1
4
2
5
3
1
4
2
5
3
1
1
4
2
5
3
1
4
2
5
3
1
4
2
2
5
3
1
4
2
5
3
1
4
2
5
3
3
1
4
2
5
3
1
4
2
5
3
1
4
4
2
5
3
1
4
2
5
3
1
4
2
5
5
3
1
4
2
5
3
1
4
2
5
3
1
1
4
2
5
3
1
4
2
5
3
1
4
2
2
5
3
1
4
2
5
3
1
4
2
5
3
3
1
4
2
5
3
1
4
2
5
3
1
4
4
2
5
3
1
4
2
5
3
1
4
2
5
5
3
1
4
2
5
3
1
4
2
5
3
1
Welk cijfer komt het minst voor?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
1
9. De uitdrukking (1 + x)(1 − ) is gelijk aan
x
1
)
x
1
(D) (x − 1)(1 − )
x
(A) (1 − x)(1 −
1
)
x
1
(E) (x − 1)(1 + )
x
(B) (1 − x)(1 +
2
(C) (x + 1)(
1
− 1)
x
10. Bij de talentenjacht “X 2 Factor” wordt een deelnemer door drie juryleden beoordeeld.
Elk jurylid geeft als score 0, X of X 2 . De eindscore is het product van deze drie
beoordelingen. Hoeveel eindscores zijn er mogelijk?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
11. De rechthoek in de figuur is opgebouwd uit 30 vierkantjes met oppervlakte 1. Hoe groot is de oppervlakte van het gekleurde gebied?
(A) 6
(B) 6,5
(C) 7
(D) 7,5
(E) 8
12. Bij het uitbreken van een griepepidemie in een school is 10 % van de leerlingen ziek.
Een week later is nog eens 10 % van de overige leerlingen ziek en is ook 10 % van
de oorspronkelijk zieke leerlingen weer gezond. Hoeveel procent van de leerlingen is op
dat moment ziek?
(A) 16 %
(B) 17 %
(C) 18 %
(D) 19 %
(E) 20 %
13. De som van twee opeenvolgende gehele getallen is 12 kleiner dan het drievoud van het
grootste van die twee getallen. Als x het kleinste van die twee getallen is, dan geldt
(A) x + (x + 1) + 12 = 3(x + 1)
(B) x + (x + 1) + 12 = 3x + 1
(C) (x − 1) + x − 12 = 3x
(D) x + 2x − 12 = 3x + 1
(E) x + (x + 1) − 12 = 3(x + 1)
14. In het vierkant in de figuur zijn een diagonaal en een
willekeurige snijlijn gegeven. Wat is het verband tussen
de hoeken α en β?
α
β
(A) α = 2β
(D) α − β = 45◦
(B) α + β = 90◦
(E) α − β = 30◦
(C) α + β = 180◦
15. Een spel kaarten bevat 26 rode en 26 zwarte kaarten en wordt in twee stapeltjes
verdeeld. Het eerste stapeltje bevat drie keer zoveel kaarten als het tweede en het
bevat ook dubbel zoveel rode als zwarte kaarten. Hoeveel zwarte kaarten bevat het
tweede stapeltje?
(A) 0
(B) 3
(C) 6
3
(D) 7
(E) 13
16. Op hoeveel nullen eindigt het product van alle priemgetallen kleiner dan 100?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
17. Als x een geheel getal is, dan is x 2 − x − 1
(A) oneven
(D) negatief
(B) even
(E) deelbaar door drie
(C) positief
√
√
√
3−1 √
1
3+1
3
18. Als je de getallen
, 3 − 1, ,
en
van klein naar groot rangschikt,
3
3
3
3
dan is het middelste getal gelijk aan
√
√
√
√
1
3−1
3+1
3
(B)
3−1
(C)
(E)
(A)
(D)
3
3
3
3
19. De punten A, B, C, D, E, F, G en H
zijn hoekpunten van twee kubussen
met een gemeenschappelijk zijvlak,
zoals in de figuur. Welke van volgende rechten snijden elkaar?
B
•
•
A
(A) AB en CD
(D) CD en GH
•
•
(B) AB en EF
(E) EF en GH
C
(C) AB en GH
20. Als x 4 − 3 = 0, dan is (x − 1)(x 8 + x 9 + x 10 + x 11 ) gelijk aan
(A) 9
(B) 12
(C) 15
(D) 18
(E) 21
21. Een rechthoek is verdeeld in zes vierkanten zoals in de figuur. Twee van deze
vierkanten zijn congruent en de lengte
van de zijde van het kleinste vierkant is
1. Wat is de lengte van de zijde van het
grootste vierkant?
1
(A) 5,5
(B) 6
(C) 6,5
4
(D) 7
•
H
•
E
•
D
G
•
F
(E) 7,5
22. De langste twee zijden van een rechthoekige driehoek meten 255 en 257. Wat is de
lengte van de kortste zijde?
(A) 2
(B) 4
(C) 8
(D) 16
(E) 32
23. Lesley en An staan met de ruggen tegen elkaar en stappen allebei 6 meter vooruit en
draaien 90◦ naar links. Daarna stappen ze allebei achtereenvolgens 5, 4, 3, 2 en 1
meter vooruit waarbij ze telkens tussen twee afstanden 90◦ naar links draaien. Hoe ver
staan ze op het einde uit elkaar?
(A) 0 m
(B) 5 m
(C) 10 m
(D) 15 m
(E) 21 m
24. Een lift vertrekt vanaf verdieping 0 (gelijkvloers), gaat naar verdieping 30 en maakt
hierbij zeven tussenstops. De lift stopt op de verdiepingen 1, 3, 6, 10, 15, 21 en 28,
maar niet in deze volgorde. Hij daalt slechts éénmaal tussen twee stops. De afstand
tussen twee verdiepingen is 3 m en de lift legt in totaal 156 m af. Naar welke verdieping
daalt de lift?
(A) 1
(B) 3
(C) 6
(D) 10
(E) 15
25. Een vergadering met vijf aanwezigen, uitsluitend elfen of trollen (minstens één van elke
categorie), wordt bijgewoond door Aislin, Bevan, Calum, Deirde en Erin. Trollen liegen
altijd, elfen spreken altijd de waarheid. Aan de vergadertafel gebeuren de volgende
uitspraken:
Aislin: “Calum en Deirde zijn allebei elfen.”
Bevan: “Ik behoor niet tot dezelfde categorie als Calum.”
Calum: “Bevan en Deirde zijn allebei elfen.”
Deirde: “Ik ben een elf.”
Erin: “Aislin is een elf.”
Hoeveel trollen zitten er aan tafel?
(A) 1
(D) 4
(B) 2
(C) 3
(E) Het aantal is niet eenduidig te bepalen.
26. Een toren bestaat uit 2013 dozen. In de bovenste doos zit 1 appel en in de andere
dozen zit telkens 1 appel meer dan in de doos erboven. Elke keer als spookje Boe
over de toren vliegt, neemt hij de bovenste doos met a appelen en de doos daar net
onder met b appelen weg. Hij eet 2b − ab appelen op en zet een doos met de rest van
de appelen weer op de toren. Uiteindelijk blijft er van de toren maar één doos over.
Hoeveel appelen zitten in die doos?
(A) 0
(B) 1
(C) 2
5
(D) 2013
(E) 20132
27. Wat is de grootste gemene deler van 2012 en 1220 ?
(A) 2
(B) 22
(C) 212
(D) 220
(E) 224
28. Bij een dobbelsteen is de som van de ogen op overstaande zijvlakken gelijk aan 7.
Acht dobbelstenen met afmetingen 1 × 1 × 1 worden in een doorzichtig doosje met
afmetingen 4 × 2 × 1 geplaatst. Het maximale aantal zichtbare ogen is dan
(A) 108
(B) 114
(C) 124
(D) 132
(E) 156
29. Onderzoekers bestudeerden hoe gelukkig mensen worden door spullen te kopen. Ze
meten deze geluksfactor op een schaal van 0 (niet gelukkig) tot 1 (heel gelukkig). Als
een bepaalde aankoop geluksfactor x heeft en een andere aankoop geluksfactor y , dan
is x + y − xy de geluksfactor van beide aankopen samen. Welke van volgende aankopen
maakt het minst gelukkig?
(A) een aankoop met geluksfactor 0,88
(B) twee aankopen met geluksfactoren 0,7 en 0,7
(C) twee aankopen met geluksfactoren 0,1 en 0,9
(D) twee aankopen met geluksfactoren 0,4 en 0,8
(E) drie aankopen met geluksfactoren 0,5, 0,5 en 0,5
30. Als in het product
B C
D C
×
A A A
verschillende letters verschillende cijfers voorstellen, dan is A + B + C + D gelijk aan
(A) 18
(B) 19
(C) 20
6
(D) 21
(E) 22