Holey Fibers

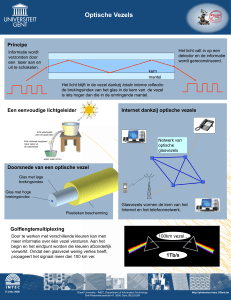
Holey Fibers
door Niels Thijssen en Wouter Vandenbussche iov prof. Jan Engelen
Inhoudtafel
Inhoudtafel .............................................................................................................................................. 1
Inleiding ................................................................................................................................................... 1
Werkingsprincipe..................................................................................................................................... 2
Het lassen van microgestructureerde fiber............................................................................................. 5
Eigenschappen......................................................................................................................................... 7
Toepassingen ......................................................................................................................................... 10
Referenties ............................................................................................................................................ 11
Inleiding
Glasvezel is al meer dan 40 jaar een vertrouwd begrip geworden in de telecommunicatie sector.
Volgens Moores wet zullen verwerkingsnelheden elke 18 maanden verdubbelen. De groeiende vraag
naar transmissie capaciteit van informatie zal het belang van glasvezel dus alleen nog maar doen
toenemen. Glasvezel heeft zijn werking te danken aan het inwendig reflecteren van het licht in een
glazen kern. Oorspronkelijk bestonden monomode vezels, en multimodevezels.
De ontwikkeling naar nieuwe soorten glasvezels is echter nooit stilgevallen. Al een tiental jaar is er
onderzoek naar holle vezels of micorgestructureerde vezels. Deze vezels verschillen van de
conventionele door de luchtgaten in de axiale richting. De twee types holle vezels berusten op
reflectie of op het “fotonische bandgap effect” (verder uitgelegd). Deze vezels bieden vele voordelen
ten op zichte van de conventionele vezels. Dit geeft aanleiding tot heel wat toepassingen waarin de
vezels van nut kunnen zijn. Ondanks het onderzoek naar holle vezels nog lang niet afgerond is,
voorspellen wetenschappers dat holle vezels de toekomst van steeds grotere informatie overdracht
kunnen verzekeren.
Werkingsprincipe
Structuur van holle kabels
Microgestructureerde vezel en conventionele vezels bestaan allebei uit een kern en een mantel,
figuur 1. Onder een microscoop wordt het verschil tussen beide pas echt duidelijk. Bij een holle
vezels is er in de mantel een periodische gaten structuur gemaakt. De gaten liggen in de axiale
richting van de vezel (figuur 1). Er zijn 2 types te onderscheiden, die verschillen in principe en
werking. Er zijn vezels met een hoge brekingsindex die een vaste glazen kern hebben, en vezels met
een lage brekingsindex met meestal een holle kern. De vezel met een vaste een hoge brekingsindex
wordt photonic crystal fiber (PCF) genoemd, die met lage brekingsindex photonic bandgap fiber (PBF)
(Figuur 2).
Figuur 1. Microgestructureerde optische vezel [1]
Figuur 2. Links: photonic crystal fiber (PCF) [4] ; Rechts photonic bandgap fiber (PBF) [5]
2
Fotonisch crystal fiber (hoge effectieve brekingsindex) (PCF) [3]
Zoals al eerder aangegeven heeft deze vezel een vaste glazen kern met een hoge brekingsindex.
Rondom de kern zitten er axiaal gerichte microkanalen (luchtgaten) met diameters gaande kleiner
dan 1 micron. De diameter, afstand (periodiciteit) en structuur van vezel zijn bepalend voor de
eigenschappen. De werking van de vezel berust op het principe van totale interne reflectie,
vergelijkbaar met klassieke vezels. De werking wordt hieronder verduidelijkt.
Figuur 3. Werking van totale interne reflectie. [3]
Figuur 4. Kritische hoek θc. [3]
Wanneer een lichtstraal een overgang maakt naar een medium met een hogere index wordt deze
straal naar de normaal toe gebogen. Bij een bepaalde hoek, de kritische hoek θ c, zal de invallende
lichtstraal gebroken worden op een hoek van 90° t.o.v. de normaal (langs het brekingsvlak). Wanneer
het licht dus onder een hoek groter dan de kritische hoek het brekingsvlak raakt, zal er geen licht
meer in het tweede medium intreden. Dit is bekend als totale interne reflectie. De kritische hoek kan
berekend worden aan de hand van de wet van Snell:
Sin(θ 1)*n1=sin(θ 2)*n2
Met θ2 = 90°
Resulteert:
θc = θ1 = arcsin(n2/n1)
Voor glas(n1=1.5) en lucht (n2=1) bedraagt de kritische hoek dan 41,8°
3
Toch zijn er opmerkelijke verschillen tussen deze vezel, en de conventionele glasvezels. Bij
conventionele vezels wordt het verschil in brekingsindex bereikt door een verschillend materiaal te
nemen voor kern en mantel. Bij fotonische crystal vezels zorgen de gaten in de mantel voor het grote
brekingsindex verschil. Het index contrast is zo groot dat zelfs de gemiddelde optische vermogens
geconcentreerd kunnen worden in een zeer kleine sectie. Aan de hand van de microstructuur kan
ook nog eens de dispersie eigenschappen worden bijgestuurd.
Door in te spelen op de pitch (gat-tot-gat afstand) kunnen ook het aantal modes in de vezel bepaald
worden. De modes die zich in de vezel kunnen voortplanten zijn afhankelijk van de brekingsindex en
van de pitch. Zo zullen selectieve golflengtes zich kunnen propageren door de vezel, en andere weer
niet.
Een veel gebruikte vorm van fotonisch crystal fibers zijn deze met een driehoeks kanalen structuur.
Er is een gat weggelaten in het midden van de vezel om de kern te vormen. Bij deze vezels geldt dat
zolang de verhouding tussen de luchtgaten diameter en de pitch kleiner is dan 0.45, zal de vezel
enkel een single mode propageren, ongeacht de grote van de kern.
Fotonische bandgap fiber (lage effectieve brekingsindex) (PBF)
Zoals al uit de titel af te leiden valt, heeft de kern van deze vezel een lagere brekingsindex dan de
mantel eromheen. Het principe van totale inwendige reflectie gaat hier dus duidelijk niet op. Er
bestaan 2 mogelijkheden om zo een vezel te bekomen. Een mogelijkheid is een fotonisch cristal vezel
te nemen, en de luchtgaten op te vullen met vloeibaar kristal die een veel hogere brekingsindex
heeft als de glazen kern. Een tweede mogelijkheid is het gebruik maken van een holle kern, die op
zijn beurt dan ook weer een lagere brekingsindex heeft als de omliggende mantel.
Een fotonische bandgap kan bekomen worden door een periodische structuur van hoge
brekingsindexmaterialen. Er kan aangetoond worden (uit de wetten van Maxwell) dat er periodische
structuren bestaan die samen alle radiale propagaties blokkeren en de axiale propageren. Licht kan
alzo door de vezel gegidst worden, waarbij de ontsnapping ervan geblokkeerd wordt door de
fotonische bandgap.
De fotonische bandgap wordt ook wel eens vergeleken met de elektronische bandgap, waarbij enkel
elektronen met een bepaalde range aan energie zijn toegelaten. Deze toegelaten energiebanden zijn
van elkaar gescheiden door de zogenaamde bandgaps. De bandgap kan dus ook voorgesteld worden
als een verboden energie zone voor elektronen die zich in het kristal willen voortplanten. Zowel bij
electronische als fotonische bandgaps kan dit bereikt worden door een periodieke structuur.
Hierdoor zou dan ook een vezel met een fotonische bandgap in het zichtbare licht spectrum niet
bruikbaar zijn. Door de kern, die van glas of lucht bestaat, te vernauwen zullen er nieuwe toegelaten
toestanden in de bandgap ontstaan. Het gevolg hiervan is alleen frequenties die perfect match met
de nieuwe toestanden zich in de vezel kunnen propageren. Hierdoor kan het licht ook niet anders
dan alleen door de centrale kern zich voortplanten.
4
Het lassen van microgestructureerde fiber
Door het revolutionair design en de ongewone fysische eigenschappen is er grote interesse in
microgestructureerde fibers (MOF). De moeilijkheid van het lassen van MOF’s zorgde aanvankelijk
voor groot obstakel, en legde een druk op de MOF technologie.
De hoge verliezen op een splitsing tussen MOF’s en conventionele vezels of tussen 2 MOF’s kunnen
worden toegeschreven aan twee oorzaken. Vooraleerst zal er tussen de MOF’s en de conventionele
vezels een inherente modus mismatch optreden ten gevolge van de intrinsieke werking van de
afzonderlijke vezel. De tweede oorzaak is te wijten aan het ineenstorten van de luchtgaten in de
buurt van de splitsing. Dit ten gevolge van lokale smelting van de vezel, waardoor de vezel zijn
vermogen om licht te geleiden verliest.
Hieronder zijn testen beschreven voor het lassen van MOFs vezels. Er wordt gebruik gemaakt van
een commerciële elektrische-boog lasser. De testen beschrijven de overgang van vervolgens MOF
compatibel met de standaard single mode fiber SSMF (hier de SMF28) en deze van MOF naar MOF.
De testen zijn gebeurd met oog op treksterkte en extra verlies in de las.
MOF-SMMF fusie
De las wordt gerealiseerd met een boog van korte tijd en een zwak vermogen. Testen wezen uit dat
de beste resultaten werden bekomen met boog duur van 0.40, 0.45 of 0,50 seconden. In figuur 5
wordt de schematische opbouw van het experiment gegeven.
Figuur 5. Experimentele opstelling [2]
De verliezen worden gemeten voor en na de lassen. Voor een boogduur van 0,40 en 0,45 seconden
vinden we typische verliezen van 0,7 en 1,1 dB. De verliezen zijn vermoedelijk hoofdzakelijk toe te
wijzen aan de mismatch tussen MOF en SMMF. De experimenteel gemeten waarden van verlies
vinden we in figuur 6. Een nog groter boogduur leidt al vlug tot verliezen van 1.5 tot 2.5 dB.
Figuur 6. Meetresultaten van de MOF-SMMF fusie; treksterkte vs de verliezen. De bolletjes voor een
boogduur van 0.50s, de kruisjes voor 0.45s, de vierkantjes voor 0.40s [2]
5
Een compatibele berekende MOF die dezelfde verliezen geeft als experiment geeft een pitch van (gat
tot gat afstand) van 3.6 micron en een gatdiameter van 1.0 micron. Bij verhoging van de gatdiameter
tot 1.3 micron worden verliezen van 1.6dB berekend. Toch leert de praktijk dat dit betere resultaten
geeft voor de las. Figuur 7 toont dat de luchtgaten ineenstorten in de buurt van de las, met gevolg
dat een bredere mode vezel een betere matching geeft aan de SSMF mode. De verliezen van de las
zijn dus zeer gevoelig aan de gatdiameters en structuur van de vezels. Een nog groter boogduur leidt
al vlug tot verliezen van 1.5 tot 2.5 dB. De grote boogduur zorgt voor een plaatselijke ineenstorting
van de vezel die het licht niet meer kan geleiden (figuur 7).
Figuur 7. Links: SSMF-MOF las zonder ineenstorting (boogduur 0.4s). Rechts: SSMF-MOF las met
ineenstorting van de luchtgaten (boogduur 0.5s) [2]
De testen van treksterkte worden gedaan met hoge voorzichtigheid. Het risico van kleine
beschadigingen of kraken in de vezel rond de las zouden de resultaten sterk beïnvloeden. De
resultaten kunnen wederom in figuur 6 terug gevonden. We vinden en trekkracht tussen de 20 en 80
kpsi. Voor een referentie van een las tussen twee SSMF’s worden trekkrachten bekomen van 110 tot
200 kpsi.
MOF – MOF fusie
Hetzelfde experiment wordt gedaan voor MOF-MOF fusies. Mits de juiste uitlijning (ook rotatie) van
de vezels worden de verliezen minimum. In figuur 8 zijn de resultaten van de test opgegeven. Er zijn
MOF’s lassen mogelijk tot minimum verliezen van 0.08 dB. Al zijn de verliezen over een grote gebied
verspreid. De grootste verliezen zijn ook hier nog steeds te wijten aan het ineenstorten van de
luchtgaten. Naast de mismatch van de geometrie van de twee vezels is een tweede oorzaak de
mismatch tussen de verschillende ineenstorting van de gaten in de twee vezels. Ook de mate van het
identiek zijn van de lasbogen kan in vraag gesteld worden. Het wordt dus snel duidelijk dat het
maken van een degelijke las tussen MOF’s zeer gevoelig is, nog meer dan een MOF-SSMF fusie.
Figuur 8. Meetresultaten van de MOF-MOF fusie; treksterkte vs de verliezen. De bolletjes voor een boogduur
van 0.50s, de kruisjes voor 0.45s, de vierkantjes voor 0.40s [2]
6
Om de treksterkte te waarborgen is er een gebied nodig in de vezel zonder gaten. Het ineenstorten
van de gaten kan ook de treksterkte bevorderen. De hier gebruikte test had relatief kleine gaten en
een dikke mantel rondom wat de treksterkte bevorderde.
Besluit
Het realiseren van een MOF las is dus een zeker niet onoverkoombaar probleem. Het zou allesinds
geen reden mogen zijn voor het onderzoek naar MOF vezels te stoppen. Ook alternatieve methodes
voor het lassen zijn zeker nog de moeite waard om verder te onderzoeken, bv het CO2 laserlassen.
Eigenschappen
In deze paragraaf bespreken we de verschillende eigenschappen van holle vezels. Er zal ook
regelmatig verwezen worden naar een gewone monomode glasvezel om het verschil duidelijk te
maken.
Zoals al vermeld zijn er twee soorten glasvezels [10].
De propagatie bij het eerste type steunt op totale interne refelectie. Men noemt dit type holle vezel
ook wel “photonic crystal fiber” (PCF). Het voordeel van dit type vezel ten opzichte van zijn
tegenhanger is dat vele van zijn optische eigenschappen (bv dispersie) kunnen zorgvuldig aangepast
worden naar gelieve door te spelen met parameters (zie verder).
Bij het tweede type holle vezel steunt de propagatie niet op reflectie maar op het fysisch verschijnsel
van fotonische bandgap. Deze vezels noemt men “photonic bandgap fiber” (PBF). Licht propageert
door het centrum. Dit centrum is vaak van lucht. Het grote voordeel hiervan is dat dispersie en
absorptie kunnen geëlimineerd worden.
We zullen vooral de eigenschappen van PCF bespreken omdat deze in praktijk het meest gebruikt
worden.
Sterke niet-lineariteit
Holle vezels beperken licht tot een zeer kleine oppervlakte binnenin de fiber doordat er een groot
contrast is tussen de brekingsindices van lucht en glas. De oorzaak van een hoge niet-lineariteit van
de PCF vezels is dus de combinatie van een abrupte overgang in brekingsindex en een hoge
intensiteit van licht in het centrum. Door het bijsturen van de microstructuur van de vezels kunnen
we nu optische eigenschappen van de vezel aanpassen. Hieronder wordt op enkele van deze
eigenschappen dieper ingegaan.
Verliezen
Een klassieke monomode glasvezel heeft zijn fysische limiet in zake verlies bijna bereikt. Veel minder
dan 0.2 db/km zal niet lukken dankzij Rayleigh verstrooiing. Hierdoor is het ook niet mogelijk om
grote golflengtes (> 10µm) te gebruiken.
Het grootste verschil inzake verlies zit in het lekverlies. Dit verlies is veroorzaakt door het plooien van
de vezel. Zoals verder (bij EMA) zal besproken worden daalt dit verlies exponentieel met het aantal
lagen gaten. Zo blijkt [6] dat het verlies van een PCF (0.205 dB/km) ongeveer gelijk is aan een
standaard monomode glasvezel, maar dat het lekverlies door plooiing een factor 800 kleiner is.
7
Dispersie
Dispersie is een van de belangrijkste karakteristieken van een glasvezel. Ze is namelijk
verantwoordelijk voor pulsverbreding. Met andere woorden dispersie is verantwoordelijk voor het
transmissiedebiet van de glasvezel. Hoe meer dispersie, hoe breder de puls bij de ontvanger en dus
hoe meer overlap tussen verschillende pulsen. Als we nu die dispersie kunnen beperken of zelfs
elimineren, kunnen we de signaalfrequentie opdrijven.
Er zijn twee verschillende soorten dispersie: materiaal dispersie en golfpropagatiedispersie.
Deze laatste soort is veroorzaakt door de golflengte afhankelijke brekingsindexverandering van de
gaten. Deze dispersie wordt groot als de gaten groot zijn of de core klein. In figuur 9 zien we de
dispersie ifv de golflengte voor verschillende gatdiameter/gatafstand verhoudingen. We merken dat
voor de verhouding 0.2 en 0.3 er geen dispersie is bij 1550nm. Bovendien zien we dat we zones met
een negatief dispersie kunnen gebruiken om dispersiecompensatie te doen.
Figuur 9: dispersie regimes voor verschillende gatdiameter/pitch verhoudingen. [8]
In figuur 10 zien we een voorbeeld van een glasvezel opgebouwd uit 13 lagen van gaten rond de
core. De core zelf is met germanium gedopeerd zodanig dat bij een golflengte van 1550nm de
dispersie nul is. Door de afstand tussen de gaten aan te passen kunnen we helling van de –duidelijk
zeer niet-lineaire – dispersiecurve aanpassen.
Figuur 10: Een dwarsdoorsnede van een PCF met 13 gaten (a). De overeenkomstige dispersie en EMA
grafieken voor verschillende dimensies (b). [1]
8
Effectieve mode oppervlak
Het effectieve mode oppervlak (EMA) is een maat voor de oppervlak een bepaalde mode effectief
voorkomt. Het EMA van holle vezels is gemakkelijk een factor 10 kleiner dan normale glasvezels. Zo is
een EMA van minder dan 2 µm² mogelijk [1].
Het grote voordeel van een kleine EMA – naast de oorzaak van sterkte niet-lineariteiten zoals eerder
vermeld – is dat de lichtbundel sterk geleid wordt. Dit wil zeggen dat bocht effecten en andere
externe storing zwak zijn. Een nadeel echter van een kleine EMA is echter dat “confinement losses”
(vrij vertaald als verliezen door opsluiting) toenemen.
Het toevoegen van meer lagen van gaten kan dit verlies verminderen. Zoals te zien is op figuur 10
kan men de EMA ook beïnvloeden door het aanpassen van de afstand tussen de gaten. Men kan het
verlies zo zelfs beperken tot 0.2 db/km. Meestal is dit echter niet nodig omdat door de sterke nietlineariteit de lengte van de kabel beperkt blijft (< 10m) een verlies van 1db/km toelaatbaar is.
In plaats van het zeer klein maken van EMA, kan met ook opteren voor het zeer groot (> 1000µm²)
maken van de EMA. Dit heeft als voordeel de niet-lineariteiten weg te werken. Dit soort vezels zijn
minder gevoelig voor beschadiging en worden bv gebruikt om intense pulsen te versterken.
Afsnij golflengte
Vanaf een bepaalde golflengte zal een monomode glasvezel multimode worden. Deze golflengte is
vooral afhankelijk van de kern diameter. De golflengtes buiten het bereik zullen sterk verzwakt
worden, vooral dankzij lekverlies. Met holle vezels is echter mogelijk om een zeer breed bereik te
verkrijgen waarbinnen monomode propagatie mogelijk is. In het geval van monomode propagatie
moeten we de genormaliseerde frequentie (V) kleiner zijn van 2.4. In formulevorm wordt gegeven
door
. In normale glasvezels is V niet naar boven begrenst omdat enkel
golflengte significant afneemt. In holle vezels echter varieert de brekingsindex van de cladding ook
en is V naar boven begrenst. In figuur 9 wordt de genormaliseerde frequentie van twee holle fibers
uitgezet ifv de frequentie voor twee verhoudingen van gatgrootte/gatafstand. En zoals duidelijk op
de figuur blijft V voor een zeer groot interval binnen de grenzen van 0.8 en 2.4. Dit soort vezels
noemen ze ook “endlessly single-mode fibers”.
Figuur 11: Genormaliseerde frequentie van twee holle vezels. Let op de begrensde genormaliseerde
frequentie. [9]
9
In sommige toepassingen echter zijn monomode vezels met grote kerndiameter nodig. Dit kan
bereikt worden door een zeer klein verschil in brekingsindex tussen cladding en core. Deze methode
heeft echter enkele nadelen zoals een groot lekverlies. Men kan de gewenste vezels ook bekomen
door PCF met een groot IMA.
Besluit
Na onderzoek van de verschillende eigenschappen kunnen we concluderen dat het grote voordeel
van holle vezels hun niet-lineariteit is. Door deze niet lineaire karakteristiek kunnen we de optisch
eigenschapen van de vezel aanpassen naar believen. Zo kunnen we bijvoorbeeld de dispersie nul
maken of het lekverlies drastisch inperken.
Toepassingen
In deze paragraaf bespreken we enkele belangrijke toepassingen van holle vezels. Deze nieuwe soort
vezel krijgt meer en meer toepassingen. Zo worden ze gebruikt als niet-lineaire omvorming, in
telecomtoepassingen, als sensor, in kwantumoptica, als lichtversterker, … [7]
We lichten enkele specifieke toepassingen hieronder wat meer toe.
Supercontinuüm generatie [7]
Supercontinuüm generatie is een proces waarbij laserlicht omgezet wordt in licht met een breed
spectrum. Hierbij wordt wel meestal spatiale coherentie behouden. Deze verbreding is meestal
bewerkstelligd door optische pulsen door een sterk niet-lineair apparaat te sturen. Als apparaat
wordt vaak een stuk PCF gebruikt. Deze is uitermate geschikt vanwege zijn dispersiekarakteristiek.
Zelfs met een laag ingangsvermogen kan een zeer breed spectrum gerealiseerd worden. Op figuur 12
zie je het resultaat van een dergelijk apparaat. Een stukje vezel (0-2 mm) zorgt voor een verbreding
van het spectrum. De kleur geeft de intensiteit van de bepaalde golflengte (logaritmisch) weer.
Een zeer belangrijke toepassing van supercontinuüm is fluorescentie microscopie. Hierbij worden
bepaalde organische of anorganische elementen zichtbaar gemaakt door licht van een bepaalde
golflengte erop te laten schijnen. Het is dus gewenst om een beeld op te nemen van meerdere
fluorescenties gelijktijdig.
Figuur 12: Verbreding van het zichtbaar spectrum na een bepaalde (verticale as) doorgang door een holle
vezel. [7]
Hoog vermogen vezels [7]
Hoog vermogen vezels worden gebruikt om vermogenrijk laserlicht te transporteren. Dit laserlicht
wordt bijvoorbeeld in industriële toepassingen gebruikt om te snijden of lassen. Bij hoge vermogens
komen er nieuwe problemen bij, zoals het opwarmen van de vezel of het beschadigen ervan.
Om opwarming te verminderen kan met de EMA vergroten. Bij klassieke vezels zullen de lekverliezen
10
snel toenemen. Een holle vezel kan hiervoor een oplossing bieden. Zij het in een licht aangepast
vorm. Hieronder een dwarsdoorsnede van een veel gebruikte verel: de “double-clad fiber”. Op de
werking hiervan gaan we niet dieper in.
Figuur 13: Dwarsdoorsnede van een holle vezel voor hoog vermogen geleiding. [7]
Referenties
[1]
O. Bjarklev, J. Broeng, “Microstructerd fibers: Design and Applications”, Photonics Spectra
(Feb 2006)
[2]
B. Bourliaguet, C. Paré, F. Émond, A. Croteau, ” Microstructured fiber splicing”, Optics
Express, Vol. 11 Nr 25, (2003)
[3]
http://www.fiberoptics4sale.com/Merchant2/optical-fiber.php
[4]
http://www.nrl.navy.mil/techtransfer/fs.php?fs_id=97
[5]
http://www.rdmag.com/
[6]
http://www.hitachi-cable.co.jp/ICSFiles/afieldfile/2005/12/01/h01.pdf
[7 ]
http://www.rp-photonics.com/
[8]
http://www.lightreading.com/document.asp?doc_id=21449
[9]
http://www.iap.unibe.ch/publications/download/2719/en/2719.pdf
[10]
W. Mannstadt, B. Drapp, B. Hoppe, D. Sprenger, “Microstructured Fiber: Out of the lab and
put to use”, Photonics Spectra (Sep 2005)
[11]
P. Rusell, “Photonic Crystal Fibers: A Historical Account”, IEEE LEOS Newsletter (Okt 2007)
11