newton 4-5H K1 Licht uitwerkingen basisboek

K1 Optica
Lichtbeelden | havo
Uitwerkingen basisboek
K1.1 INTRODUCTIE
1
[W] Experiment: Spiegels en spiegelbeelden
2
[W] Voorkennistest
3
Waar of niet waar?
a Waar
b Niet waar: Ook glanzende oppervlakken zoals een glimmende auto kunnen als
spiegel gebruikt worden.
c Waar
d Waar
e Niet waar: Een voorwerp heeft kleur als er het licht dat er op schijnt de juiste kleur
bevat.
f
Niet waar: In het maanlicht zie je bijna geen kleuren, omdat het licht van de maan te
zwak is. Hierdoor kunnen je ogen de kleuren niet goed onderscheiden.
4
Zie figuur.
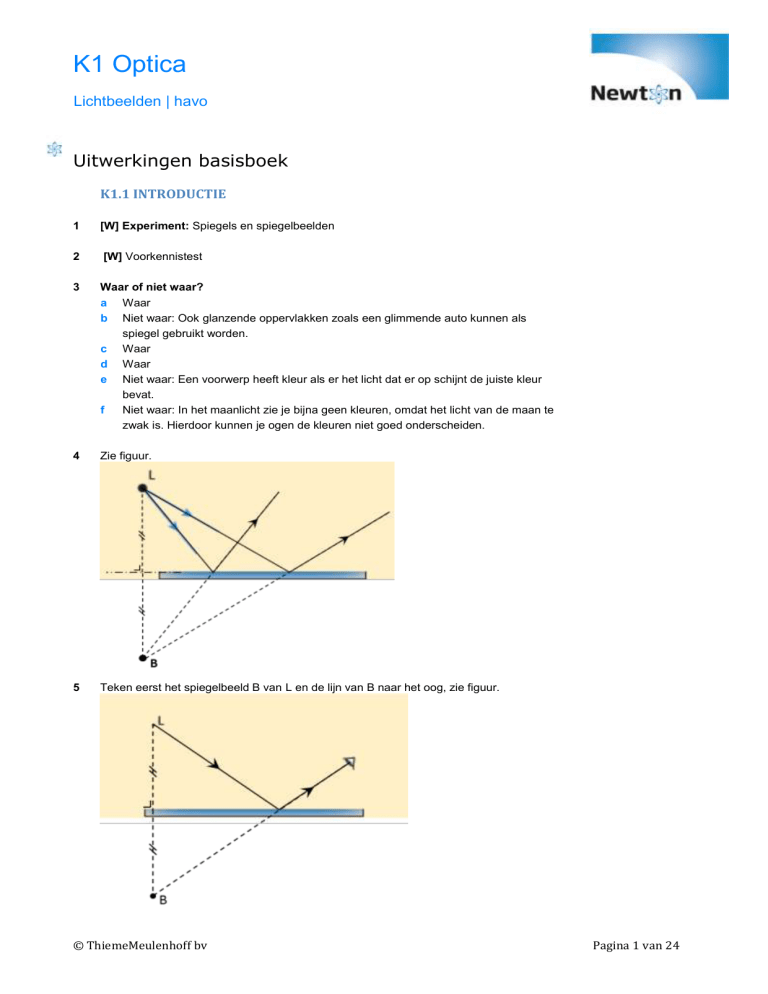
5
Teken eerst het spiegelbeeld B van L en de lijn van B naar het oog, zie figuur.
© ThiemeMeulenhoff bv
Pagina 1 van 24
6
a
Zie figuur.
b
Zie figuur.
c
Zie bovenstaande figuur: De lichtstraal met één pijltje erin die loopt van L naar de
spiegel, loopt evenwijdig aan de lichtstraal met één pijltje erin die loopt van spiegel S 2
naar omhoog. Hetzelfde geldt voor de lichtstraal met twee pijltjes erin.
De lichtstralen worden rechtstreeks gereflecteerd door de combinatie van S1 en S2.
Merk op dat de onderste lichtstraal na reflectie de bovenste is geworden. Met deze
spiegel kun je dus jezelf zien zoals anderen jou zien (dus niet in spiegelbeeld).
d
e
7
a
Zie figuur.
© ThiemeMeulenhoff bv
Pagina 2 van 24
b
c
8
Nee, de automobilist ziet de auto’s die hem inhalen niet.
Met een bolle spiegel is het gezichtsveld veel groter en kan de automobilist ook zien
wat er links achter hem zit.
Wat je op de foto links ziet, zie je in de spiegel rechts.
9
a
b
c
Rood-wit-blauw zie je als zwart-blauw-blauw.
Rood-wit-blauw zie je als rood-rood-zwart.
Rood-wit-blauw zie je als zwart-groen-zwart.
K1.2 HET MAKEN VAN BEELDEN
10
[W] Experiment: Lenzen en lensbeelden
11
[W] Experiment: Camera Obscura
12
Waar of niet waar?
a Niet waar: Een bolle lens breekt de lichtstralen van een bundel (meer) naar elkaar toe.
Dat is de convergerende werking van de bolle lens.
b Niet waar: Een holle lens breekt de lichtstralen van een bundel (meer) van elkaar af.
Dat is de divergerende werking van de holle lens
c Niet waar: De plek waar lichtstralen die uit één voorwerpspunt komen elkaar na een
bolle lens snijden, is het beeldpunt.
d Waar
e Waar
f
Waar
g Waar
h Niet waar: Met een zwakke positieve lens kun je zowel een heel klein als een heel
groot beeld maken.
i
Waar
13
a
b
c
14
Als het voorwerp op brandpuntsafstand van de lens staat, komt er een evenwijdige
bundel uit een bolle lens.
Als het voorwerp verder van het brandpunt afstaat, komt er een convergente bundel
uit de lens.
Als het voorwerp tussen het brandpunt en de lens in staat, komt er een divergente
bundel uit de lens.
De lichtbundel die uit één punt komt wordt door een negatieve lens alleen nog maar verder
uit elkaar gebogen en kan dus nooit in één punt bij elkaar komen achter de lens. Zie
figuur.
© ThiemeMeulenhoff bv
Pagina 3 van 24
15
a
b
c
d
e
f
Teken een lichtstraal die door het midden van de lens gaat, deze verandert niet van
richting. Zie onderstaande figuur links.
L1 en L2 staan op gelijke afstand van de lens, dus het beeld van L 2 ontstaat ook op
dezelfde afstand van de lens als B1. Er ontstaat een scherp beeld van L2 op het
scherm.
Teken een lichtstraal door het midden van de lens en een lichtstraal die vòòr de lens
evenwijdig aan de hoofdas gaat. Deze gaat na de lens door het brandpunt. Het
snijpunt van de twee lichtstralen is het beeldpunt B2.
L2 staat nu verder van de lens af, waardoor de lichtstralen iets minder divergent (meer
evenwijdig) op de lens vallen. Hierdoor ontstaat het beeldpunt B 2 dichter bij de lens.
In de figuur is goed te zien dat op het scherm de lichtstralen niet in één punt
samenkomen. Er ontstaat een “vlek” op het scherm. Het beeld is dus onscherp.
Teken een scherm dat door B1 en B2 gaat.
16
a
b
c
17
Als het voorwerp dichter bij de lens komt te staan, is de rode lichtbundel die op de
lens valt meer divergent. Het punt waar de stralen elkaar na de lens snijden ligt dan
verder weg.
Als het voorwerp te dicht bij de lens staat, is de lichtbundel die van het voorwerp
afkomt zo divergent, dat de lens de stralen niet genoeg naar elkaar toebuigt. De
lichtbundel is dan achter de lens nog steeds divergent en kan dus niet samen komen
in één beeld.
Vanaf de brandpuntsafstand.
Oriëntatie:
De stippellijnen zijn lijnen die loodrecht staan op het spiegeloppervlak. Gebruik dat de
hoek van inval gelijk moet zijn aan de hoek van terugkaatsing.
Uitwerking:
a Zie figuur.
© ThiemeMeulenhoff bv
Pagina 4 van 24
Zie figuur.
b
Bolle spiegels hebben een divergerende werking.
18
[W] Experiment
19
Eigen antwoord.
20
a
b
c
Het maakt niet uit vanaf welke kant het licht op de lens valt. Een evenwijdige
lichtbundel vanaf de andere kant komt ook in een brandpunt samen.
Ja.
De lichtstraal evenwijdig aan de hoofdas gaat na breking door het brandpunt achter
de lens. Als je nu de loop van de lichtstraal omdraait, gaat de lichtstraal voor de lens
door het brandpunt en na de lens evenwijdig aan de hoofdas.
a
Zie figuur.
b
c
Zie bovenstaande figuur.
Het beeld is groter dan het voorwerp, dus vergroot.
a
Zie figuur.
21
22
© ThiemeMeulenhoff bv
Pagina 5 van 24
b
c
De lichtstralen vallen meer divergent op de lens, dus het beeld is groter dan het
voorwerp.
Zie figuur.
a
Zie figuur.
b
De lichtstralen vallen meer convergent op de lens, dus het beeld is kleiner dan het
voorwerp.
Als het voorwerp heel ver weg staat zullen de lichtstralen evenwijdig invallen. Ze
komen dan samen in het brandpunt. Het beeld is dan zo klein als een punt geworden.
23
c
24
Oriëntatie:
Teken eerst een lichtstraal van L’ naar B’. Deze gaat door het midden van de lens. Teken
vervolgens de lens en tenslotte de andere twee constructiestralen met de brandpunten.
Uitwerking:
Zie figuur.
25
a
Meet de brandpuntsafstand van F2 tot de lens op en plaats het brandpunt F1 op
dezelfde afstand voor de lens. Teken vervolgens de lichtstralen. Zie figuur.
© ThiemeMeulenhoff bv
Pagina 6 van 24
26
b
Zie figuur.
c
Het beeld is even groot als het voorwerp.
1
1
𝑆 = 𝑓 = 0,035 = 29 dpt.
27
1
𝑆
1
−0,80
a
𝑓= =
= −1,25 = −1,3 m.
b
Het minteken geeft aan dat het een negatieve lens is.
a
Zie figuur.
b
Zie bovenstaande figuur.
c
𝐿b = 1,5 cm dus 𝑁 =
d
𝑏 = 7,5 cm dus
a
7,2/3 = 2,4 en 10,8/3=3,6 dus de dia is 2,4 bij 3,6 cm.
b
N= 3=
c
Zie figuur, schaal 1:10.
28
𝑏
𝑣
=
𝐿b
1,5
= 1,0
𝐿v
7,5
= 1,5.
5,0
= 1,5.
29
b
v
60

v
v = 20 cm.
f = 1,5 ∙ 10 = 15 cm dus S =
© ThiemeMeulenhoff bv
1
f
=
1
0,15
= 6,7 dpt.
Pagina 7 van 24
30
[W] Experiment: De lenzenformule
31
[W] Experiment: De negatieve lens en het virtuele beeld
32
[W] Holle en bolle spiegels
33
a
1
𝑣
1
1
1
1
1
b
𝑁=
c
Schaal 1:2 dus het beeld is 0,7∙2 = 1,4 cm groot.
d
Eigen antwoord.
a
𝑁 = 𝑣  5 = 𝑣  𝑏 = 5 ∙ 𝑣.
+ 𝑏 = 𝑓  9,5 + 𝑏 = 5,6  𝑏 = 13,6 = 14 cm.
𝑏
𝑣
=
13,6
9,5
= 1,4.
34
b
𝑏
1
𝑣
1
𝑏
1
1
1
1
6
1
+ 𝑏 = 𝑓  𝑣 + 5𝑣 = 10  5𝑣 = 10  𝑣 = 12 cm. De afstand tussen lens en
scherm is dus 𝑏 = 5 ∙ 𝑣 = 5 ∙ 12 = 60 cm.
K1.3 OPTISCHE APPARATEN
35
[W] Experiment: Pupil meten
36
[W] Experiment: Onderzoek aan jouw oog
37
Waar of niet waar?
a Niet waar: Door te accommoderen wordt de ooglens boller gemaakt door het
aanspannen van de oogspier.
b Waar
c Niet waar: Bij een fotocamera worden alleen de voorwerpen die op dezelfde afstand
van de lens staan als waarop is scherp gesteld ook scherp afgebeeld.
d Niet waar: Als je ‘wegdroomt’ zie je de dingen die ver weg zijn scherp.
e Niet waar: Met je pupil regel je de hoeveelheid licht die in je oog komt.
38
a
b
c
d
Bij een camera is b ongeveer gelijk aan f. De beeldafstand is bij een mobieltje erg
klein omdat het mobieltje erg plat is. Dus is de brandpuntsafstand ook erg klein.
Het beeld wordt scherp afgebeeld op een beeldchip die kleiner is dan het voorwerp.
Het beeld is dus verkleind.
Bij een camera is v erg groot. De lichtstralen uit één voorwerp vallen vrijwel evenwijdig
op de lens, zodat het beeld in het brandvlak wordt gevormd.
Mobieltje is ongeveer 1,0 cm dik, dus de brandpuntsafstand is ongeveer 1,0 cm. 𝑆 =
1
𝑓
1
= 0,010 = 100 dpt.
© ThiemeMeulenhoff bv
Pagina 8 van 24
39
a
b
c
40
De sterkte van de ooglens.
De beeldafstand.
Ja, als de ooglens heeft scherp gesteld op een bepaald voorwerp, kunnen de
voorwerpen op ongeveer dezelfde afstand nog scherp gezien worden door de pupil te
verkleinen. Door het kleiner maken van de pupil worden de ‘vlekjes’ van de onscherpe
voorwerpen op het netvlies kleiner en zie je dus scherper.
Dan geldt: tan 𝛼
=
hoogte voorwerp
afstand tot voorwerp
=
0,020
1,0
= 0,020  𝛼 = 1,1°.
41
1
1
a
𝑓 = 𝑆 = 125 = 0,00800 m = 0,800 cm.
b
De voorwerpsafstand is groot, waardoor de lichtstralen uit één voorwerpspunt vrijwel
evenwijdig invallen op de lens. De beeldafstand is dan vrijwel gelijk aan de
brandpuntsafstand.
c
𝑁=
d
𝑁=
a
Een gewone lens is bol aan de buitenkant. Bij een fresnellens wordt alleen de bolle
oppervlakte van de lens gebruikt, de massieve binnenkant wordt weggelaten.
Hierdoor is een fresnellens net zo sterk als een gewone lens, maar wel veel platter.
Zie figuur.
𝑏
𝑓
0,800
≈ =
= 0,0032.
𝑣
𝑣
250
𝐿b
𝐿b
 0,0032 =
 𝐿b =
𝐿v
185
0,59 cm.
42
b
c
Ja, als de lamp precies in het brandpunt staat is de lichtbundel na de lens een sterke,
evenwijdige lichtbundel.
a
b
Met een negatieve lens vergroot je het gezichtsveld van de kassière.
Zie figuur.
43
44
Eigen antwoord.
45
Waar of niet waar?
a Waar
b Niet waar: Bij een loep kijk je naar een virtueel, vergroot en rechtopstaand beeld.
© ThiemeMeulenhoff bv
Pagina 9 van 24
46
Zie figuur.
47
a
b
Ze heeft zonder bril een grotere gezichtshoek.
Ze kan zonder bril meer details waarnemen.
a
In het donker valt er te weinig licht op de kegeltjes in je ogen die de kleuren
waarnemen. De kegeltjes reageren niet als er te weinig ‘energie’ van het licht is, zodat
je geen kleuren waarneemt.
De kegeltjes zitten op je gele vlek. Door naast de ster te kijken valt het ligt niet op je
gele vlek, maar ernaast, waar de staafjes zitten. Met je staafjes reageren wel bij
weinig licht.
48
b
49
a
b
Deze persoon is verziend en oudziend (zijn oogas is te kort en zijn lens niet meer zo
elastisch).
Het positieve (lees)gedeelte van deze bril zit onderin.
50
a
b
c
51
Als het hoornvlies boller wordt gemaakt vervangt dit een bolle lens van een bril. Deze
operatie wordt dus bij verziendheid gedaan.
Als het hoornvlies minder bol wordt gemaakt vervangt dit een holle lens van een bril.
Deze operatie wordt dus bij bijziendheid gedaan.
Iemand die oudziend is heeft een minder elastische ooglens en kan dus minder goed
accommoderen. Als de het hoornvlies boller gemaakt zou worden, zou deze persoon
niet goed meer in de verte kunnen kijken.
[W] Experiment: Een verrekijker bouwen
52
a
b
c
d
De microscoop bestaat uit een buis met meerdere lenzen. Het is dus het rechter
instrument.
Er komt dan een evenwijdige lichtbundel uit de lens.
Bij gebruik van de gecombineerde lens kun je met een ongeaccommodeerd oog heel
dicht bij de lens komen. Als je bij gebruik van slechts één lens dichterbij de lens komt
ga je het beeld wazig zien.
De twee lenzen zijn samen een sterkere lens dan één lens apart. Je ziet het beeld dus
groter bij de twee lenzen samen.
53
a
b
c
De afstand tussen het voorwerp en de loep is kleiner dan de brandpuntsafstand.
De lichtstralen lopen na de lens divergent.
Omdat de lichtstralen divergent lopen, lijken ze niet achter, maar voor de lens bij
elkaar te komen. Daardoor lijkt het beeld van het voorwerp groter te zijn.
© ThiemeMeulenhoff bv
Pagina 10 van 24
54
Je moet erop letten dat de diameter van het objectief groot genoeg is, zodat er meer licht
de kijker binnenkomt.
55
Daar zal de waarnemer weinig van merken, want hij heeft zijn ogen scherp gesteld op de
maan. Hij ziet hoogstens een wazig vlekje. Het lukt de waarnemer ook niet om scherp te
stellen op de vlieg, de vlieg zit daarvoor veel te dicht bij het objectief.
56
Oriëntatie:
Construeer eerst het (virtuele) beeld B van L. Voor het oog lijkt de lichtbundel te komen
van dit virtuele beeld B.
Uitwerking:
57
a
De lichtstralen van een ver weg gelegen voorwerp vallen vrijwel evenwijdig in, zodat
het beeld in het brandpunt. De brandpuntsafstand van de lens is: 𝑓
1
𝑆
= =
1
54,0
=
0,0185 m = 1,85 cm. De afstand van de ooglens tot het netvlies (2,00 cm) is groter
b
dan de brandpuntsafstand dus het beeld komt vòòr het netvlies terecht. Door te
accommoderen wordt de lens sterker en de brandpuntsafstand nog kleiner. Het lukt
dit oog dus niet om een ver weg gelegen voor werp scherp op het netvlies af te
beelden.
Om ver weg gelegen voorwerpen scherp op het netvlies te krijgen moet de
brandpuntsafstand van de ooglens 2,00 cm zijn. De sterkte van de ooglens is dan:
𝑆=
1
𝑓
=
1
0,0200
= 50 dpt.
c
Deze persoon moet contactlenzen met een negatieve sterkte hebben, om ver weg
gelegen voorwerpen weer scherp op het netvlies te krijgen.
a
De minimale sterkte is de sterkte die hoort bij een brandpuntsafstand van 22 mm:
58
1
1
=
= 45 dpt.
𝑓
0,022
𝑏
= 𝑣 = 0,073 en de beeldafstand b is 22 mm dus:
𝑆=
b
𝑁
0,073 =
22
𝑣
𝑣
=
22
0,073
=
301 m. Het nabijheidspunt ligt dus op 30 cm van de ooglens.
59
a
b
De grootte van het beeld is 5 x 1,5 = 7,5 cm.
De beeldafstand is 5 x 2,5 = 12,5 cm.
© ThiemeMeulenhoff bv
Pagina 11 van 24
c
Zie figuur.
d
e
f
Zie bovenstaande figuur.
f = 3,1 cm.
Als de persoon zijn oog 3,5 cm voor de loep houdt, lijkt voor hem het beeld op een
afstand van 3,5 + 12,5 = 16 cm te staan.
Hij moet de afstand tussen het voorwerp en de loep iets vergroten.
g
60
𝑏
25
a
𝑁 = 𝑣 = 0,025 = 1000 = 1,0 ∙ 103 .
b
Omdat het beeld veel verder van de lens af staat, en een voorwerp dat verder weg is
lijkt kleiner.
Ja, dat klopt.
c
61
[W] Experiment: Adaptatie van je ogen aan het duister
62
[W] Experiment: Verschillende soorten ogen
K1.4 EIGENSCHAPPEN VAN LICHT
63
[W] Experiment: Lichtsnelheid meten
64
[W] Experiment: Absorptie van licht
65
Waar of niet waar?
a Waar
b Niet waar: De lichtsnelheid in glas is kleiner dan in lucht.
c Waar
d Niet waar: Als fotonen geabsorbeerd worden, wordt de energie van de fotonen
afgegeven en daarmee zijn de lichtdeeltjes verdwenen.
© ThiemeMeulenhoff bv
Pagina 12 van 24
e
f
g
h
i
j
Niet waar: De frequentie van rood licht is ongeveer twee keer zo klein als de
frequentie van blauw licht.
Waar
Niet waar: Breking van licht wordt veroorzaakt doordat licht zich als een golf gedraagt.
Waar
Niet waar: De verschillende kleuren van de regenboog die je ziet, komen allemaal uit
andere regendruppels.
Niet waar: Voor de kleur met de grootste brekingsindex is (in de betreffende stof) de
lichtsnelheid het kleinst.
66
a
b
Omdat de lichtsnelheid is enorm groot is in vergelijking met de snelheden waaraan de
mens gewend is. Het heeft lang geduurd voordat de juiste apparatuur er was om zo’n
grote snelheid te meten.
We kunnen met sterke telescopen sterren waarnemen waarvan het licht al miljarden
jaren geleden is uitgezonden. De levensduur van een ster is ook van die orde grootte,
dus is de kans groot dat deze sterren al zijn verdwenen op het moment dat het licht
ervan ons bereikt.
a
b
c
De UV-straling wordt voor een heel groot deel al door de atmosfeer geabsorbeerd.
Je hand wordt warm.
De fotonen worden geabsorbeerd en geven daarbij hun energie af.
a
b
c
d
Blauw licht wordt het meeste gebroken.
Bij rood licht is de lichtsnelheid het grootst in water.
De lichtsnelheid is in glas kleiner dan in water.
Als de lichtstraal van water naar glas gaat, wordt de lichtsnelheid kleiner. Er is dan
breking naar de normaal toe.
a
b
𝑠 = 𝑣 ∙ 𝑡  10 ∙ 103 = 3,00 ∙ 108 ∙ 𝑡  𝑡 = 3,3 ∙ 10−5 s.
67
68
69
Het signaal moet in ieder geval naar de satelliet en weer terug, zie figuur.
Bereken met Pythagoras: 𝑠 = √𝑅aarde 2 + (𝑅aarde + ℎ)2 met 𝑅aarde = 6371 km (zie
Binas)  𝑠 = √63712 + (6371 + 36000)2 = 42847 km.
De af te leggen weg is dus 2 ∙ 42847 = 85695 km  𝑡 =
2∙𝑠
𝑐
=
85695
300000
= 0,29 s.
Dat duurt dus minimaal 0,29 s.
70
a
b
Glas absorbeert licht met de frequentie van het ultraviolette licht.
Kwartsglas laat licht met de frequentie van het ultraviolette licht door.
© ThiemeMeulenhoff bv
Pagina 13 van 24
c
Om te voorkomen dat mensen die in het licht van een halogeenlamp komen
blootgesteld worden aan ultraviolet licht, wordt dit licht tegengehouden met een extra
laag gewoon glas.
a
Zie figuur.
b
c
Zie bovenstaande figuur.
Het lijkt of het bordje, dat op de bodem ligt, hoger ligt. Dus in werkelijkheid is het
zwembad dieper dan je waarneemt.
71
72
Zie figuur.
73
Zie figuur.
74
Het licht wordt naar de normaal toe gebroken, dus lijkt het voor de waarnemer alsof het
licht van hoger komt. De sterren lijken hoger te staan dan de werkelijke plek aan de hemel.
Zie figuur.
© ThiemeMeulenhoff bv
Pagina 14 van 24
75
[W] Experiment: Breking van lucht naar perspex
76
[W] Brekingsindex
77
Eigen antwoord.
78
De verschuiving hangt af van de dikte van de plaat, de brekingsindex van het glas, de
hoek van inval en de frequentie van het invallende licht.
79
In een vooraanzicht is het rietje een rechte lijn. Rechts daarnaast zit het oog. Door de
breking van de lichtstralen bij het wateroppervlak lijkt het rietje minder diep in het water te
zitten. Lichtstralen die onder het wateroppervlak uit de zijkant van het glas komen, lijken
juist van dieper te komen. De ronding van het glas heeft ook nog invloed op het geheel.
Zie figuur.
80
a
b
c
[𝐸] = [ℎ] ∙ [𝑓]  J = J∙s∙Hz en 1 Hz = 1 s-1 dus J = J∙s∙s-1
𝐸foton = ℎ ∙ 𝑓 = 6,626 ∙ 10−34 ∙ 1 ∙ 1026 = 7 ∙ 10−8 J.
a
𝜆 = 𝑓 = 1880∙106 = 0,160 m.
Als het gammafoton wordt geabsorbeerd, brengt de energie van het foton een deeltje
in beweging. Dit deeltje botst weer tegen andere deeltjes aan die andere deeltjes
botsen ook weer verder.
81
b
c
d
e
82
𝑐
1
4
3,00∙108
𝜆 = 0,040 m.
𝐸foton = ℎ ∙ 𝑓 = 6,626 ∙ 10−34 ∙ 1880 ∙ 106 = 1,246 ∙ 10−24 J.
Deze fotonen hebben weinig energie in vergelijking met zichtbaar licht.
2,6 GHz = 2600 MHz, dat is een hogere frequentie en dus een kortere golflengte dan
de radiogolven van de DECT telefoon.
Oriëntatie:
Zoek in Binas de brekingsindex voor rood licht in water op: n = 1,33.
𝑐
Gebruik 𝑛 = 1 waarbij c1 de lichtsnelheid in lucht is en c2 de lichtsnelheid in water.
𝑐2
Uitwerking:
1,33 =
83
3,00∙108
 𝑐water
𝑐water
= 2,26 ∙ 108 m/s.
Oriëntatie:
Bereken eerst de snelheid van het licht in de glasvezelkabel met
𝑐
𝑛 = 𝑐1 en vervolgens de
2
© ThiemeMeulenhoff bv
Pagina 15 van 24
tijd met 𝑠 = 𝑣 ∙ 𝑡.
Uitwerking:
3,00∙108
1,5 = 𝑐
glasvezel
 𝑐glasvezel = 2,0 ∙ 108 m/s.
7 ∙ 106 = 2,0 ∙ 108 ∙ 𝑡  𝑡 = 3,5 ∙ 10−2 = 0,04 s.
84
a
Oriëntatie:
Bereken eerst hoeveel energie de laserpointer in 2,0 seconde afgeeft met 𝐸 = 𝑃 ∙ 𝑡 en
reken vervolgens uit hoeveel fotonen dit zijn.
Uitwerking:
𝐸 = 1 ∙ 10−3 ∙ 2,0 = 2 ∙ 10−3 J dus dat zijn
b
c
2∙10−3
3∙10−19
= 6,7 ∙ 1015 = 7 ∙ 1015
fotonen.
Oriëntatie:
Bereken eerst hoeveel energie 100 fotonen hebben en vervolgens hoe lang de
laserpointer aan moet staan met 𝐸 = 𝑃 ∙ 𝑡.
Uitwerking:
100 fotonen leveren 100 ∙ 3 ∙ 10−19 = 3 ∙ 10−17 J  3 ∙ 10−17 = 1 ∙ 10−3 ∙ 𝑡  𝑡 =
3 ∙ 10−14 J.
Onze ogen kunnen de afzonderlijke fotonen niet waarnemen, daarvoor vallen ze veel
te kort op elkaar op ons netvlies.
85
sin 𝑖
sin 60
a
𝑛 = sin 𝑟 = sin 35 = 1,5.
b
Zie figuur.
sin 𝑖
sin 𝑖
86
𝑛 = sin 𝑟  1,60 = sin 30  sin 𝑖 = 0,80  𝑖 = 53°.
87
[W] Experiment: Breking en totale terugkaatsing
88
Totale terugkaatsing treedt op wanneer de lichtstraal van de normaal af breekt en de
invalshoek groter is dan de grenshoek g.
89
a
b
De brekingshoek is groter dan de invalshoek, dus er is breking van de normaal af. Dat
betekent dat stof B de minder dichte stof is. Stof B is lucht.
Ja, er kan totale terugkaatsing optreden bij de overgang van A naar B.
© ThiemeMeulenhoff bv
Pagina 16 van 24
c
Oriëntatie:
Totale terugkaatsing treedt op als de invalshoek groter is dan de grenshoek g. De
grenshoek is te berekenen met sin 𝑔
1
= 𝑛 en de brekingsindex n is bij breking van
een dichte stof naar lucht, te berekenen met
sin 𝑖
sin 𝑟
1
= 𝑛.
Uitwerking:
sin 22°
sin 38°
=
1
1

𝑛
𝑛
= 0,608  sin 𝑔 = 0,608  𝑔 = 37°.
Totale terugkaatsing treedt op als de invalshoek groter is dan 37°.
90
De invalshoek bij het grensvlak prisma – lucht is 45°, dat is groter dan de grenshoek (voor
o.a. glas, acryl en perspex), dus er vindt volledige terugkaatsing plaats. Zie figuur.
91
Onze ooglens werkt dankzij de breking van het licht bij de overgang van lucht naar water
(de samenstelling van de lens is ongeveer gelijk aan die van water). Als er nu voor de
ooglens ook water zit, worden de lichtstralen niet meer gebroken en kan er geen scherp
beeld op het netvlies ontstaan. Door het opzetten van een duikbril zit er wel weer een laag
lucht voor de ooglens, zodat de lichtstralen weer gebroken worden bij de overgang van de
lucht naar de ooglens.
92
a
Zie figuur.
b
1
𝑛
c
𝑛=𝑐
sin 𝑖
sin 30°
= sin 𝑟 = sin 47°  𝑛 = 1,46 = 1,5.
𝑐lucht
vloeistof
 1,46
3,00∙108
=𝑐
vloeistof
 𝑐vloeistof = 2,1 ∙ 108 m/s.
d
Kijk in Binas: de brekingsindex van rood licht bij glycerol is 1,466. Het zou hier om
glycerol kunnen gaan (misschien niet helemaal zuiver).
a
De brekingsindex van diamant bij violet licht is 2,457.
93
1
1
sin 𝑔 = 𝑛  sin 𝑔 = 2,457  sin 𝑔 = 0,4070  𝑔 = 24,02°.
© ThiemeMeulenhoff bv
Pagina 17 van 24
b
De grenshoek van diamant is veel kleiner dan van glas (ongeveer 41°). Dat betekent
dat de lichtstralen die door een diamant heen gaan veel sneller worden teruggekaatst
op het moment dat de lichtstraal het diamant zou verlaten. Er zitten dus veel meer
‘spiegeltjes’ in een diamant dan in een stuk glas dat in dezelfde vorm is geslepen.
1
1
94
sin g = n  sin 45° = n  n = 1,4.
95
Bij het eerste grensvlak lucht  glasvezel: 𝑛
sin 𝑖
sin 75°
𝑟
sin 𝑟
1
1
 sin g =
𝑔
n
1,5
= sin 𝑟  1,5 =
Bij het tweede grensvlak glasvezel  lucht: sin g
=
= 40°.
= 42° en 𝑖 =
50° dus er vindt volledige terugkaatsing plaats. Dit gaat zo door tot aan het eind van de
glasvezel en daar geldt weer: 𝑖 = 40° dus 𝑟 = 75°.
96
Perspex: n = 1,5 en g = 42°. Bij het eerste grensvlak is i = 60° dus i > g  volledige
terugkaatsing.
Bij het tweede grensvlak is i = 30° 
97
1
n
=
sin i
1

sin r
1,5
=
sin 30°

sin r
r = 49°. Zie figuur.
[W]
K1.5 LICHT IN DE RUIMTE
98
[W] Experiment: Licht ontleden
99
Waar of niet waar?
a Waar
b Waar
c Waar
d Niet waar: Het spectrum van de zon bevat, naast zichtbaar licht, ook infrarode en
ultraviolette straling.
e Waar
f
Waar
© ThiemeMeulenhoff bv
Pagina 18 van 24
100
a
b
Je kunt met beide een spectroscoop maken. Met een spectroscoop met een tralie kun
je nauwkeuriger de golflengte van het licht bepalen.
Het enige dat sterrenkundigen kunnen meten aan sterren is de straling die er van
afkomt. Die straling is uiteen te rafelen in verschillende golflengtes met behulp van
een spectroscoop.
101
a
b
c
Het gele diagram geeft het spectrum weer van zonlicht dat boven de atmosfeer is
gemeten, het rode spectrum is gemeten onder de atmosfeer. Aan het verschil tussen
het gele en het rode spectrum kun je zien welke soorten straling geabsorbeerd
worden door de atmosfeer. Daar waar dit verschil groot is, wordt veel straling
geabsorbeerd.
De theoretische stralingskromme van 5800 K geeft het spectrum weer dat een
voorwerp met een temperatuur van 5800 K zal uitzenden.
Wij zien de straling die komt van het oppervlak van de zon, dus is de 5800 K de
temperatuur van het oppervlak van de zon.
102
a
b
Het oppervlak van een dvd heeft allemaal groefjes.
Als je een dvd schuin onder een gloeilamp houdt, zie je dat het licht dat door de dvd
wordt weerkaatst is gesplitst in alle kleuren van de regenboog.
a
b
c
Rood
Geel en blauw. De temperatuur is het hoogst in het blauwe stuk, vlak bij de pit.
De kleur van een gloeilamp is geler dan de kleur van de zon. Door de lagere
temperatuur ontbreken er meer blauwe golflengtes en daardoor is het licht van de
gloeilamp geler.
a
b
c
d
Normale telescopen gebruiken zichtbaar licht.
UV- en IR-straling komen niet goed door de atmosfeer.
Radiogolven worden niet geabsorbeerd door de atmosfeer.
Om te voorkomen dat de radiogolven van onze radioapparatuur de metingen van de
radiotelescopen niet verstoren worden radiotelescopen in radiostiltegebieden
geplaatst.
IR-straling kan niet door onze huizen heen.
103
104
e
105
a
b
c
Doordat de satelliet zijn kijker niet op de aarde heeft gericht, kan het infrarood straling
van andere hemellichamen registreren (zonder verstoring van de straling van de
aarde).
Voor waarnemingen aan zichtbaar licht hoef je niet de ruimte in, want de atmosfeer
houdt het zichtbare licht niet tegen.
Een ruimtetelescoop heeft het voordeel dat het licht dat de telescoop opvangt alleen
uit de ruimte komt en niet verstoord wordt door lichtbronnen op aarde.
106
a
Infrarode straling.
© ThiemeMeulenhoff bv
Pagina 19 van 24
b
c
Het gaat om de straling van de aarde, die de aarde niet kan verlaten maar wordt
geabsorbeerd door de atmosfeer.
Bij een echte broeikas wordt de warme lucht en de infrarode straling tegengehouden
door het glas van de broeikas.
107 Eigen antwoord.
108 Een gloeilamp zendt een continu spectrum uit, een tl-buis bevat een lichtgevend gas, dat
een lijnenspectrum uitzendt.
109
a
b
c
Het lichtrendement van een lamp is het percentage lichtenergie die wordt uitgezonden
ten opzichte van de elektrische energie die de lamp verbruikt.
Het grootste deel van de straling van een gloeilamp bestaat uit IR-straling en dus
geen zichtbaar licht.
Als de temperatuur van de gloeidraad wordt verhoogd, gaat de gloeidraad sneller
kapot.
110
a
b
De maan reflecteert het licht van de zon, dus zal het spectrum van de maan dezelfde
golflengtes bevatten als het spectrum van de zon.
In de atmosfeer van Venus zitten gassen die bepaalde frequenties uit het spectrum
van de zon absorberen.
111 De temperatuur van de zonnevlekken is lager dan van de rest van het oppervlak van de
zon. Het spectrum van deze zonnevlekken zal dus meer naar rechts zijn verschoven en
daardoor minder wit zijn.
112
a
Omdat het gaat om een verhouding, kun je de intensiteit gewoon met je geodriehoek
in centimeters aflezen:
b
De verhouding
𝐼b
𝐼r
3,8
= 3,1 = 1,2.
𝐼b
geeft aan bij welke golflengte het maximum van het spectrum zich
𝐼r
bevindt en de plaats van het maximum hangt af van de temperatuur van de ster.
c
Als
𝐼b
groter is, bevindt het maximum zich meer naar links en is de temperatuur van
𝐼r
de ster hoger.
113 Meet met een spectroscoop het spectrum van de lava en bepaal aan de hand van de
stralingskromme de temperatuur van de lava.
114
a
b
c
De lijnen komen allemaal van dezelfde ster, dus schuiven alle lijnen dezelfde kant op.
Het heelal dijt uit, dus alle sterren bewegen van ons vandaan. Dat betekent dat alle
lijnen zijn verschoven naar de rode kant.
Doordat de ster van ons af beweegt, zijn de frequenties die worden gemeten lager
dan bij een stilstaande ster, net als bij een auto met sirene die van ons af beweegt.
Verschuiving naar lagere frequenties betekent verschuiving in de richting van het rode
gebied van het spectrum.
© ThiemeMeulenhoff bv
Pagina 20 van 24
115 Dat alleen ‘roodverschuiving’ is waargenomen betekent dat alle sterren van ons af
bewegen (en alle sterren ook van elkaar af bewegen). Het heelal dijt dus uit.
116
a
b
Bij een violetverschuiving beweegt het sterrenstelsel zich naar ons toe.
Bij een violetverschuiving zijn alle spectraallijnen iets richting het violette gebied
opgeschoven. Dat wil nog niet zeggen dat die spectraallijnen ook in het violette gebied
zitten. Dus het licht van de dit stelsel hoeft er niet violetachtig uit te zien.
117 Eigen antwoord
118
a
b
c
d
e
f
g
h
i
j
Een directe lichtbron geeft zelf licht, zoals bijvoorbeeld een lamp. Een indirecte
lichtbron weerkaatst het licht dat van een andere lichtbron af komt.
Gekleurde voorwerpen zie je gekleurd, doordat sommige kleuren licht worden
weerkaatst en andere kleuren worden geabsorbeerd. Het licht dat weerkaatst wordt,
bepaalt de kleur.
Een virtueel beeld is een beeld dat niet getoond kan worden op een scherm.
Het gezichtsveld is het gebied dat je via de spiegel kunt zien. Bij een vlakke spiegel
wordt de grootte van het gezichtsveld bepaald door de grootte van de spiegel en van
jouw afstand tot de spiegel.
Een positieve lens breekt de lichtstralen van een bundel meer naar elkaar toe. Als de
lichtbundel voor de lens zeer divergent is, zal de positieve lens de lichtstralen niet ver
genoeg naar elkaar toe breken om er een convergente bundel van te maken. De
bundel is dan na de lens wel minder divergent.
De sterkte van een lens is de mate waarin de lens de lichtstralen breekt. Hoe sterker
de lens, hoe meer de lens de lichtstralen zal breken.
Als een positieve lens een reëel beeld maakt, is dit altijd omgekeerd. Immers, de
constructiestraal door het optisch middelpunt van de lens komt altijd aan de andere
kant van de hoofdas terecht. Als de voorwerpsafstand kleiner is dan de
brandpuntsafstand ontstaat een virtueel beeld, dat rechtop staat.
De drie constructiestralen die worden gebruikt bij het construeren van een beeld zijn:
 de lichtstraal door het optisch middelpunt O van de lens. Deze wordt niet van
richting veranderd.
 de lichtstraal evenwijdig aan de hoofdas. Deze gaat na breking door het brandpunt
achter de lens.
 de lichtstraal door het brandpunt van de lens. De loopt na breking evenwijdig aan
de hoofdas.
Bij een positieve lens is het gevormde beeld vergroot als de voorwerpsafstand kleiner
is dan twee keer de brandpuntsafstand zit (𝑣 < 2𝑓 ). Het gevormde beeld is verkleind
als de voorwerpsafstand groter is dan twee keer de brandpuntsafstand (𝑣 > 2𝑓 ).
Als de sterkte van een lens toeneemt, wordt de brandpuntsafstand kleiner. Dit volgt
1
uit: 𝑆 = waarbij S de sterkte van de lens is en f de brandpuntsafstand.
𝑓
k
Voor de lineaire vergroting N geldt: 𝐿b = 𝑁 ∙ 𝐿v waarbij Lb de afmeting van het beeld is
en Lv afmeting van het voorwerp. De lineaire vergroting N is ook gelijk aan de
verhouding van de beeldafstand b en de voorwerpsafstand v: 𝑁
l
𝑏
= 𝑣.
Een menselijk oog stelt scherp door spieren rondom te lens aan te spannen waardoor
de ooglens boller en dus sterker wordt. Dit proces heet accommoderen.
© ThiemeMeulenhoff bv
Pagina 21 van 24
m
n
o
p
q
r
Door de diameter van de pupil te variëren, wordt de hoeveelheid licht geregeld die op
het netvlies valt.
Een spectroscoop rafelt het licht uiteen in een kleurenspectrum. In een spectroscoop
kan een prisma of een tralie zitten. Je kunt daarmee de golflengtes van de
verschillende kleuren licht bepalen.
Een gloeidraad is een hete metaaldraad. Het spectrum van een gloeidraad is een
continu spectrum.
Een foton is een reizende trilling. De energie van een foton hangt af van de frequentie
van de trilling.
Bij de overgang van lucht naar glas breekt de lichtstraal naar de normaal toe.
De brekingsindex hangt af de lichtsnelheden in beide stoffen.
119
a
Oriëntatie:
Construeer eerst het beeld B van L. Trek vervolgens een lijn van L’ door O. Het beeld
van L’ bevindt zich recht boven B.
Uitwerking:
b
Oriëntatie:
Trek eerst twee rechte lijnen van B’ via de randen van het diafragma naar de lens.
Verbind deze lijnen vervolgens met L’. Arceer het gebied tussen de lijnen.
Uitwerking:
c
De liniaal is in werkelijkheid 1,0 m. In figuur 88 is de liniaal 8,0 cm lang. Volgens de
tekst is dat 2,5 keer zo groot als het beeld dat is vastgelegd op het lichtgevoelige
materiaal. Op het lichtgevoelige materiaal is de liniaal dus
vergroting is dus 𝑁 =
© ThiemeMeulenhoff bv
0,032
1,0
8,0
2,5
= 3,2 cm lang. De
= 0,032.
Pagina 22 van 24
d
Vanwege de sterke verkleining is de afstand van de bordliniaal tot de lens (de
voorwerpsafstand) veel groter dan de beeldafstand. De beeldafstand zal in deze
situatie ongeveer gelijk zijn aan de brandpuntsafstand, dus de voorwerpsafstand moet
ook veel groter zijn dan de brandpuntsafstand van de lens.
a
Oriëntatie:
120
De brekingsindex van glas voor rood licht is 1,51 (zie Binas). Gebruik 𝑛
sin 𝑖
= sin 𝑟.
Uitwerking:
1,51 =
sin 57°

sin 𝑟
sin 𝑟 = 0,555  𝑟 = 34°.
b
Zie figuur.
c
𝑛=
d
De brekingsindex van glas voor blauw licht is iets groter: 1,52. De blauwe lichtstraal
zal dus iets sterker breken. Zie figuur.
e
De brekingsindex n is groter, dus zal de lichtsnelheid van het blauwe licht in glas cglas
kleiner zijn dan die van het rode licht.
Oriëntatie:
Bereken eerst de frequentie van het rode licht met 𝑐 = 𝜆 ∙ 𝑓 waarbij c de lichtsnelheid
is: 𝑐 = 3,00 ∙ 108 m/s.
Bereken vervolgens de energie van het foton met 𝐸foton = ℎ ∙ 𝑓 waarbij h de
constante van Planck is: ℎ = 6,626 ∙ 10−34 J ∙ s.
Uitwerking:
3,00 ∙ 108 = 700 ∙ 10−9 ∙ 𝑓  𝑓 = 4,286 ∙ 1014 Hz
dus 𝐸foton = 6,626 ∙ 10−34 ∙ 4,286 ∙ 1014 = 2,84 ∙ 10−19 J.
f
𝑐lucht

𝑐glas
1,51 =
© ThiemeMeulenhoff bv
3,00∙108
 𝑐glas
𝑐glas
= 1,99 ∙ 108 m/s.
Pagina 23 van 24
121
a
Zie figuur.
b
Elk blok heeft nu de halve dikte en zorgt dus ook voor de helft van de verschuiving
van het hele blok. Tussen de blokken in loopt de lichtstraal in de ‘normale’ richting. De
totale verschuiving is nu gelijk aan 2 keer de helft van de verschuiving van het hele
blok en is dus even groot als de verschuiving bij één blok.
© ThiemeMeulenhoff bv
Pagina 24 van 24