CMS zoektocht naar het Standaardmodel Higgs Boson met behulp

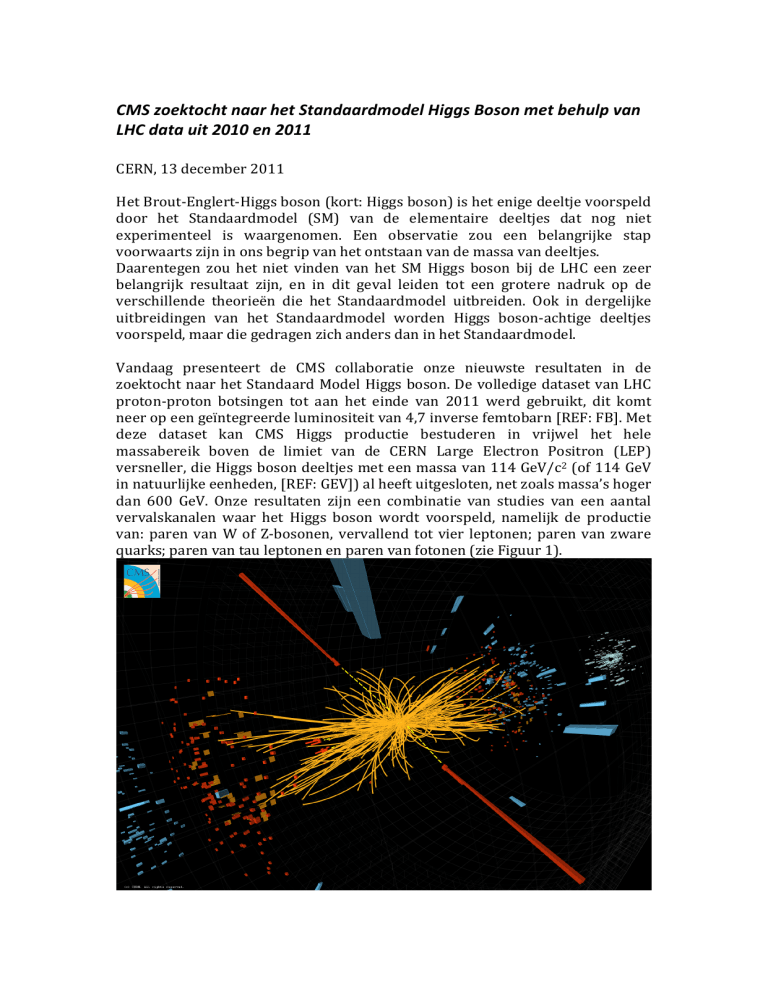
CMS zoektocht naar het Standaardmodel Higgs Boson met behulp van LHC data uit 2010 en 2011 CERN, 13 december 2011 Het Brout-­‐Englert-­‐Higgs boson (kort: Higgs boson) is het enige deeltje voorspeld door het Standaardmodel (SM) van de elementaire deeltjes dat nog niet experimenteel is waargenomen. Een observatie zou een belangrijke stap voorwaarts zijn in ons begrip van het ontstaan van de massa van deeltjes. Daarentegen zou het niet vinden van het SM Higgs boson bij de LHC een zeer belangrijk resultaat zijn, en in dit geval leiden tot een grotere nadruk op de verschillende theorieën die het Standaardmodel uitbreiden. Ook in dergelijke uitbreidingen van het Standaardmodel worden Higgs boson-­‐achtige deeltjes voorspeld, maar die gedragen zich anders dan in het Standaardmodel. Vandaag presenteert de CMS collaboratie onze nieuwste resultaten in de zoektocht naar het Standaard Model Higgs boson. De volledige dataset van LHC proton-­‐proton botsingen tot aan het einde van 2011 werd gebruikt, dit komt neer op een geïntegreerde luminositeit van 4,7 inverse femtobarn [REF: FB]. Met deze dataset kan CMS Higgs productie bestuderen in vrijwel het hele massabereik boven de limiet van de CERN Large Electron Positron (LEP) versneller, die Higgs boson deeltjes met een massa van 114 GeV/c2 (of 114 GeV in natuurlijke eenheden, [REF: GEV]) al heeft uitgesloten, net zoals massa’s hoger dan 600 GeV. Onze resultaten zijn een combinatie van studies van een aantal vervalskanalen waar het Higgs boson wordt voorspeld, namelijk de productie van: paren van W of Z-­‐bosonen, vervallend tot vier leptonen; paren van zware quarks; paren van tau leptonen en paren van fotonen (zie Figuur 1). Figuur 1: Een typische kandidaatbotsing waar twee hoog-­‐energetische fotonen zijn geproduceerd. De energie van de fotonen (weergegeven door de rode blokken) wordt gemeten in de CMS elektromagnetische calorimeter. Fotonen laten geen sporen na tot in de calorimeter, hun pad is aangegeven met de stippellijn. De andere gele lijnen zijn de gemeten sporen van geladen deeltjes die ook zijn geproduceerd in de botsing. Onze nieuwe resultaten, voor diverse statistische betrouwbaarheidsintervals [REF: CL], leiden tot uitsluiting van het bestaan van de SM Higgs boson in een breed gebied van mogelijke Higgs boson massa's: • 127 tot 600 GeV met een betrouwbaarheidsinterval van 95%, zoals aangegeven in figuur 2a; • 128 tot 525 GeV met een 99% betrouwbaarheidsinterval, en Een massa wordt gedefinieerd als "uitgesloten met 95% betrouwbaarheidsinterval" als het Standaard Model Higgs boson voor die massa in ten minste 95% van een reeks van herhaalde experimenten wel direct zou worden geobserveerd. Figuur 2a: Limiet van de uitgesloten massa van het Higgs boson SM op 95% betrouwbaarheidsinterval (indien zwarte lijn onder rode lijn). De analyse is gebaseerd op de 4,7 fb-­‐1 van proton-­‐proton gegevens verzameld door CMS in 2010 en 2011. De gearceerde banden geven de massaintervals uitgesloten door LEP, door de Tevatron op Fermilab, en nu door CMS. De stippellijn en de groene en gele banden geven de gemiddelde verwachte gevoeligheid die wordt verwacht voor deze CMS dataset. De verwachtte gevoeligheid is consistent met de waarde in de geanalyseerde data. Het CMS experiment sluit een SM Higgs boson met een massa tussen de 115 GeV en 127 GeV nog niet uit. Vergeleken met de SM voorspelling is er een klein, breed overschot van gebeurtenissen in deze massaregio (zie figuur 2b). Dit overschot is te zien in alle kanalen, maar niet significant genoeg om een conclusie te trekken over het eventuele (niet-­‐) bestaan van een Higgs boson bij deze massawaarden. Figuur 2b: De SM Higgs uitsluitingslimiet voor 95% betrouwbaarheidsinterval voor 4,7 inverse femtobarn proton-­‐proton data, voor de data verzameld door CMS in 2010 en 2011. Enkel de resultaten voor een massa tussen 110 en 160 GeV worden getoond. Met de hoeveelheid gegevens die tot nu toe zijn verzameld, is het inherent zeer moeilijk om onderscheid te maken tussen de twee hypothesen van het bestaan versus niet-­‐bestaan van een Higgs boson-­‐signaal in de lage massaregio. De waargenomen extra gebeurtenissen zijn consistent met een statistische fluctuatie van de niet-­‐Higgs achtergrondprocessen, consistent zowel inclusief als exclusief het bestaan van het SM Higgs boson. De grotere dataset die zal worden verzameld in 2012 zal de statistische onzekerheden in de lage massa regio verkleinen, waardoor we een onweerlegbare verklaring kunnen maken over de mogelijke bestaan, of niet, van het SM Higgs in deze massaregio. De data is compatibel met een SM Higgs boson hypothese met een massa in de buurt van 124 GeV of minder, maar met een statistische significantie van minder dan 2 standaarddeviaties (2σ) vergeleken met de bestaande niet-­‐Higgs achtergrond, nadat het zogenaamde “Look-­‐Elsewhere Effect” [REF: LEE] in aanmerking is genomen. Dit is ruim onder de significantie die in de elementaire deeltjesfyisca traditioneel wordt geassocieerd met resultaten die de tand des tijds doorstaan. Als we de hypothese testen dat de geconstateerde excessen een eerste hint is van de aanwezigheid van de SM Higgs boson, vinden we dat de hoeveelheid geproduceerde Higgs-­‐achtige botsingen ("werkzame doorsnede" ten opzichte van de SM, σ/σSM) in overeenstemming is met verwachtingen, voor elke vervalskanaal, maar met grote onzekerheden. Echter, de lage statistische significantie betekent dat de data redelijkerwijs net zo goed kan worden geïnterpreteerd als fluctuaties van de achtergrond. Om een solide conclusie te kunnen trekken, hebben we ten minste tweemaal onze huidige gegevens nodig. Dit sample verwachten wij te verzamelen tijdens de 2012 proton-­‐proton run van de LHC. Referenties: [REF: FB] http://news.stanford.edu/news/2004/july21/femtobarn-­‐721.html [REF: GEV] http://nl.wikipedia.org/wiki/Elektronvolt#De_elektronvolt_als_eenheid_van_ma
ssa De electronvolt is een eenheid van zowel massa als energie, door gebruik van E = mc2. Het is zeer gebruikelijk om zogenaamde ‘natuurlijke eenheden’ te gebruiken, waar c wordt gedefineerd als 1, zodat electronvolts als een directe massaeenheid kan worden gebruikt. [REF: CL] http://nl.wikipedia.org/wiki/Betrouwbaarheidsinterval Een betrouwbaarheidsinterval is een statistische methode die de fractie voorspelt dat een testresultaat ook werkelijk kan worden gemeten. Bijvoorbeeld, een betrouwbaarheidsinterval van 95% betekent dat na 100 metingen ook 95 metingen met de verwachtingen overeenstemmen. [REF LEE] http://cms.web.cern.ch/news/should-­‐you-­‐get-­‐excited-­‐your-­‐data-­‐let-­‐
look-­‐elsewhere-­‐effect-­‐decide