Hoofdstuk 3 - Transformaties

bladzijde 70
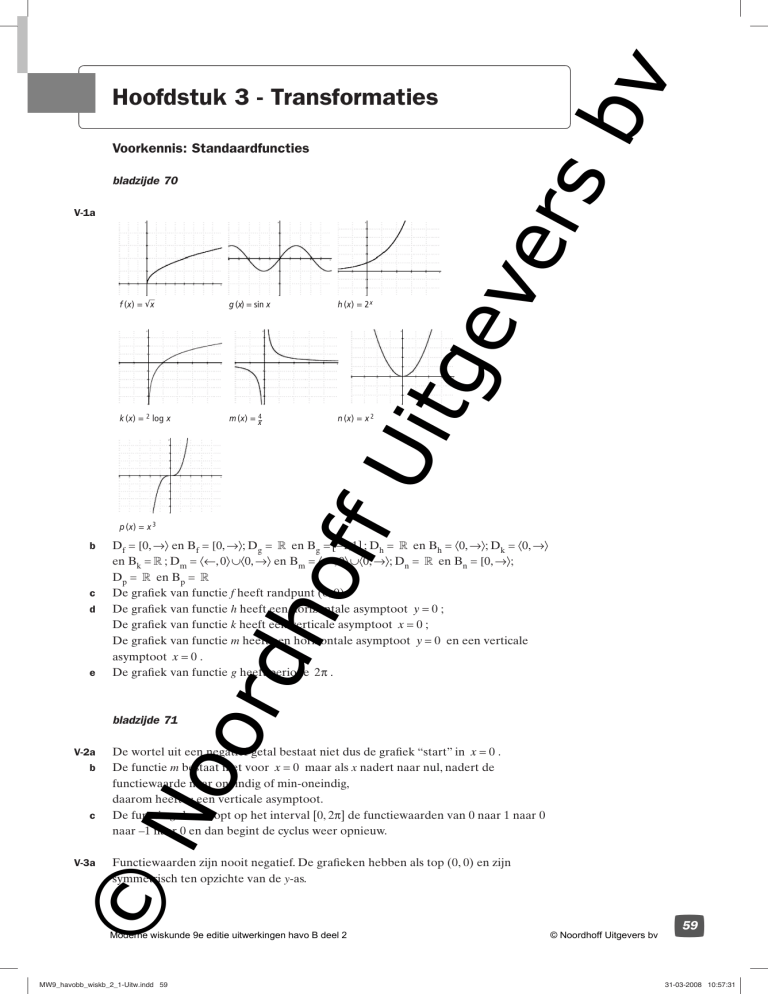
V-1a
k (x) = 2 log x
m (x) = x4
p (x) = x 3
c
d
e
Df = [0, →〉 en Bf = [0, →〉; Dg =  en Bg = [ −1, 1] ; Dh =  en Bh = 〈0, →〉; Dk = 〈0, →〉
en Bk =  ; Dm = 〈←, 0〉 ∪〈0, →〉 en Bm = 〈←, 0〉 ∪〈0, →〉; Dn =  en Bn = [0, →〉;
Dp =  en Bp = 
De grafiek van functie f heeft randpunt (0, 0).
De grafiek van functie h heeft een horizontale asymptoot y = 0 ;
De grafiek van functie k heeft een verticale asymptoot x = 0 ;
De grafiek van functie m heeft een horizontale asymptoot y = 0 en een verticale
asymptoot x = 0 .
De grafiek van functie g heeft periode 2π .
dh
b
n (x) = x 2
or
h (x) = 2x
Ui
tg
g (x) = sin x
off
f (x) = x
er
sb
v
Voorkennis: Standaardfuncties
ev
Hoofdstuk 3 - Transformaties
bladzijde 71
b
c
Functiewaarden zijn nooit negatief. De grafieken hebben als top (0, 0) en zijn
symmetrisch ten opzichte van de y-as.
©
V-3a
De wortel uit een negatief getal bestaat niet dus de grafiek “start” in x = 0 .
De functie m bestaat niet voor x = 0 maar als x nadert naar nul, nadert de
functiewaarde naar oneindig of min-oneindig,
daarom heeft m een verticale asymptoot.
De functie g doorloopt op het interval [0, 2π] de functiewaarden van 0 naar 1 naar 0
naar –1 naar 0 en dan begint de cyclus weer opnieuw.
No
V-2a
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 59
© Noordhoff Uitgevers bv
⁄
59
31-03-2008 10:57:31
c
V-4a
b
c
V-5
a
b
c
V-6a
b
Voor g > 1 zijn de kenmerken hetzelfde.
Voor 0 < g < 1 is de grafiek van f afnemend dalend met de x-as als horizontale
asymptoot en de grafiek gaat altijd door (0, 1).
Voor 0 < g < 1 is de grafiek van k afnemend dalend met de y-as als verticale
asymptoot en de grafiek gaat altijd door (1, 0).
ev
Alle grafieken zijn puntsymmetrisch ten opzichte van (0, 0). Als x negatief is, is de
functiewaarde negatief. Als x positief is, is de functiewaarde positief.
Alle grafieken gaan door (0, 0) en (1, 1).
Plot steeds de grafieken van f en g en laat de grafische rekenmachine vervolgens de
oplossingen berekenen.
t ≈ −0, 77 ; t = 2 en t = 4. De functie f stijgt op den duur het snelst.
t ≈ −0, 90 ; t ≈ 1, 14 en t ≈ 29, 21 . De functie f stijgt ook hier op den duur het snelst.
t ≈ 1, 01 en t ≈ 20, 95 . De functie f stijgt op den duur het snelst. Denk er wel aan om
functie g in te voeren als
log( x) : log(2) .
Ui
tg
b
Als x < −2 of x > 2 heeft p( x) = x 2 de meeste invloed omdat 1 dan heel snel naar
x
nul nadert.
In de buurt van x = 0 wordt q( x) = 1 groot positief of groot negatief terwijl x 2 juist
x
naar nul nadert en dus weinig invloed heeft.
off
er
sb
v
Hoofdstuk 3 - Transformaties
3.1 Grafieken verschuiven
bladzijde 72
b
2ab
dh
De coördinaten van het punt waar de raaklijn aan de grafiek horizontaal loopt zijn:
s: (0, 0); t: (–2, 0); u: (3, 5); v: (–4, –7); w: (0, 10).
De grafiek van functie t ontstaat door de grafiek van functie s 2 naar links te
schuiven.
De grafiek van functie u ontstaat door de grafiek van functie s 3 naar rechts en 5 naar
boven te schuiven.
De grafiek van functie v ontstaat door de grafiek van functie s 4 naar links en 7 naar
beneden te schuiven.
De grafiek van functie w ontstaat door de grafiek van functie s 10 naar boven te
schuiven.
y
or
1a
No
3
2
1
©
–1 O
1
2
3
4
5
6
7
8
9
10
x
–1
⁄
60
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 60
© Noordhoff Uitgevers bv
31-03-2008 10:57:35
c
d
e
f
er
sb
v
Hoofdstuk 3 - Transformaties
g( 7) = 7 − 3 = 2
f ( x) = g ( 7) = 2 geeft x = 2 dus x = 4
x = 17 − 3 = 14 dus x = 14
x = a − 3 dus x = a − 3
3a
b
4a
b
c
k( x) = 3x+ 3 ; m( x) = 3 log( x + 3) en n( x) = cos( x + 3)
t ( x) = 3x− 2π − 2 ; r( x) = 3 log x − 2 π − 2 en s( x) = cos( x − 2 π) − 2
(
)
5a
b
c
6a
b
c
d
De standaardfunctie is 1 .
x
De grafiek van de standaardfunctie heeft x = 0 en y = 0 als asymptoten. De grafiek
van f heeft x = −3 en y = 5 als asymptoten.
De standaardgrafiek is 3 naar links en 5 omhoog geschoven.
Hier wordt standaardfunctie x bedoeld.
Randpunt (0, 0) is verplaatst naar randpunt (1, 4).
Er is 1 naar rechts en 4 omhoog geschoven.
f ( x) = x − 1 + 4
©
De grafiek van s( x) = cos( x − 2 π) − 2 lijkt alleen naar beneden geschoven te zijn. Dat
komt omdat de grafiek precies één periode naar rechts is geschoven.
No
or
dh
off
De grafiek van functie f ontstaat door de grafiek van standaardfunctie cos x 1
omhoog te schuiven.
De grafiek van functie g ontstaat door de grafiek van standaardfunctie x 1 naar
rechts en 4 naar beneden te schuiven.
De grafiek van functie h ontstaat door de grafiek van standaardfunctie 1 1 naar
x
links te schuiven.
De grafiek van functie k ontstaat door de grafiek van standaardfunctie 2 log x 6 naar
rechts en 8 omhoog te schuiven.
-
Ui
tg
ev
bladzijde 73
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 61
© Noordhoff Uitgevers bv
⁄
61
31-03-2008 10:57:41
er
sb
v
Hoofdstuk 3 - Transformaties
3.2 Grafieken vervormen
bladzijde 74
7ab
y
9
8
7
ev
6
5
4
3
2
–1 O
–1
c
8ab
1
2
3
4
5
6
7
3
4
5
6
7
8
9
10
Ui
tg
1
11 12
g ( x) = 3 x
y
3
2
x
–1 O
1
2
–1
c
d
e
8
9
10
11
x
h(12) = 2
f ( x) = h(12) voor x = 4
f ( x) = h(34) voor x = 11 13 want 3 × 11 13 = 34
dh
off
1
or
bladzijde 75
9a
g ( x) =
1
4
b
g ( x) =
1
4
10a
b
c
11a
b
f ( x) = 2 log x horizontaal vermenigvuldigen met factor 4
c
f ( x) = 1 verticaal vermenigvuldigen met factor 2
x
x
x=
⋅ x=
1
2
x
No
g ( x) = −2 x , de grafiek van f wordt gespiegeld in de x-as.
h( x) = 2 − x , de grafiek van f wordt gespiegeld in de y-as.
Ja, ook bij g ( x) = log x is het effect hetzelfde.
f ( x) = sin x horizontaal vermenigvuldigen met factor 1
π
©
⁄
62
1
4
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 62
© Noordhoff Uitgevers bv
31-03-2008 10:57:46
e
f
12a
b
c
13a
bc
d
f ( x) = x achtereenvolgens horizontaal vermenigvuldigen met factor 13 en dan
verticaal vermenigvuldigen met factor 3
f ( x) = cos x achtereenvolgens horizontaal vermenigvuldigen met − 12 en dan
verticaal vermenigvuldigen met factor 14
f ( x) = 3x achtereenvolgens horizontaal vermenigvuldigen met 2 en dan verticaal
vermenigvuldigen met factor 2
g ( x) = 2 x + 4
Punt (0, 1) komt op punt (0, 16) dus de factor is 16.
16 ⋅ 2 x = 2 4 ⋅ 2 x = 2 x+ 4
Factor 16.
Factor 14 want h( x) = 16 x 2 = (4 x)2
g ( x) = 1 = 1 ⋅ 1 dus horizontaal met factor
4x 4 x
3.3 Transformaties combineren
bladzijde 76
14a
y
1
4
of verticaal met factor
1
4
.
6
off
ev
d
Ui
tg
er
sb
v
Hoofdstuk 3 - Transformaties
g
f
2
4
dh
3
2
–6
–5
or
1
–4 –3
–2
–1 O
1
2
3
4
5
6
x
–1
c
g ( x) = 2 + 1
Als je de volgorde omdraait krijg je hetzelfde resultaat.
No
b
©
1
x
2
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 63
© Noordhoff Uitgevers bv
⁄
63
31-03-2008 10:57:49
er
sb
v
Hoofdstuk 3 - Transformaties
y
15abc
6
2
h
4
g
3
ev
f
2
1
–5
–4 –3
–2
–1 O
1
2
3
4
–1
d
18
1
16
( x + 3)2
f ( x) = x 3 ⇒ g ( x) = f ( x) − 4 = x 3 − 4 ⇒ h( x) = 12 g ( x) = 12 ( x 3 − 4) = 12 x 3 − 2 of
f ( x) = x 3 ⇒ g ( x) = 12 f ( x) = 12 x 3 ⇒ h( x) = g ( x) − 4 = 12 x 3 − 4
In alle 3 de gevallen is de standaardgrafiek k( x) = 2 log x .
De grafiek van f ontstaat uit de standaardgrafiek door eerst horizontaal te
vermenigvuldigen met 5 en vervolgens 3 naar rechts te schuiven.
De grafiek van h ontstaat door de standaardgrafiek eerst 3 naar rechts te schuiven en
dan horizontaal te vermenigvuldigen met 5.
De grafiek van m ontstaat door de standaardgrafiek horizontaal met 5 te
vermenigvuldigen en 3 naar beneden te schuiven.
©
No
off
17ab
f ( x) = x 2 ⇒ g ( 14 x) = ( 14 x)2 = 161 x 2 ⇒ h( x) = g ( x + 3) =
De grafiek van h heeft (–3, 0) als top.
dh
x
or
16
6
Onderdeel b:
f ( x) = x ⇒ k( x + 3) = x + 3 ⇒ g ( x) = k(3 x) = 3 x + 3
Onderdeel c:
f ( x) = x ⇒ k(3 x) = 3 x ⇒ h( x) = k( x + 3) = 3( x + 3)
bladzijde 77
5
Ui
tg
–6
⁄
64
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 64
© Noordhoff Uitgevers bv
31-03-2008 10:57:51
19a
b
75 naar rechts schuiven en verticaal vermenigvuldigen met 0,8465.
600
punten
500
400
300
ev
200
100
c
d
50
100
150
200
250
hoogte in cm
Een atleet moet meer dan 75 cm hoogspringen om punten te halen.
Elke cm die de atleet hoger springt levert steeds meer punten op.
1000
punten
0
Ui
tg
0
800
600
200
0
20a
b
c
d
300
400
500
tijd in seconden
Een atleet moet sneller zijn dan 480 seconden om punten te halen.
Elke seconde die een atleet sneller loopt levert steeds meer punten op.
Op de 1500 meter krijg je P = 0, 03768(480 − 255)1,85 = 846 punten.
1,42
Met de grafische rekenmachine oplossen van 0, 8465 h − 75
= 846 levert een
hoogte op van ongeveer 205 cm.
(
)
Het randpunt is (0, 0).
Het randpunt is nu (2, –2).
De steilheid van de gegeven grafiek is veel groter.
Verticale vermenigvuldiging met factor 8 en vervolgens 2 naar rechts en 2 naar
beneden schuiven. Het functievoorschrift is dan g ( x) = 8 x − 2 − 2 .
©
No
200
dh
e
100
or
f
0
off
400
er
sb
v
Hoofdstuk 3 - Transformaties
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 65
© Noordhoff Uitgevers bv
⁄
65
31-03-2008 10:57:53
3.4 Transformaties van sinusoïden
bladzijde 78
21a
b
c
d
22a
h( x) = sin(2 x) + 0, 6
De periode van h is 12 × 2 π = π .
h(0) = 0, 6 dus (0; 0,6)
y = 0, 6 is de evenwichtslijn van de grafiek van h
ev
y
1,2
1,0
0,8
g
f
0,4
0,2
–5
–4 –3
–2
–1 O
0,2
1
2
3
–0,4
–0,6
–0,8
–1,0
–1,2
b
c
d
23a
b
c
5
6
7
x
f (0) = cos 0 = 1 dus (0, 1) ligt op de grafiek van f.
Eerst horizontaal vermenigvuldigen met factor 13 en daarna 4 naar rechts schuiven.
De periode wordt 13 keer zo groot dus 13 × 2 π = 23 π .
g(0) = cos 3(4 − 4) = cos 0 = 1
off
4
Ui
tg
0,6
–7 –6
er
sb
v
Hoofdstuk 3 - Transformaties
24a
Het maximum is 20 en het minimum is –10.
b
c
d
e
or
No
De periode is 80 dus b = 2 π = 401 π .
80
Om de grafiek bij x = 60 te laten beginnen moet de standaardgrafiek g ( x) = sin x 60
naar rechts schuiven dus c = 60.
f ( x) = 5 + 15 sin 401 π( x − 60)
Om te beginnen bij x = −20 moet c = −20 zijn dus f ( x) = 5 + 15 sin 401 π( x + 20) .
©
f
d = 20 + −10 = 5
2
a = 20 − 5 = 15
⁄
66
dh
De periode van h is 4 × 2 π = 8 π en de grafiek gaat onder andere door (–1, 1).
De periode van k is 12 × 2 π = π en de grafiek gaat onder andere door (0,3; 0).
De periode van l is 14 × 2 π = 12 π en de grafiek gaat onder andere door ( 1 12 , 1).
Functie l is ook te schrijven als l( x) = cos 4( x − 1 12 ) .
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 66
© Noordhoff Uitgevers bv
31-03-2008 10:57:59
bladzijde 79
26a
b
Voor de eerste grafiek geldt f ( x) = d + a sin b( x − c) met d =
De periode is π dus b = 2ππ = 2
en de grafiek ‘start’ bij x = 0 dus c = 0 .
f ( x) = 1 + sin 2 x
d = −40 + −10 = −25 en a = −10 − (−25) = 15
2
De periode is 20 dus b = 2 π = 101 π . f (0) = −10 dus het maximum ligt bij x = 0 , de
20
grafiek is dan 14 periode naar links geschoven (net als bij de tweede grafiek van
opdracht 25) dus c = −5 .
f ( x) = −25 + 15 sin 101 π( x + 5)
f (0) = −40 dus het minimum ligt bij x = 0 , de grafiek is nu 14 periode naar rechts
geschoven dus c = 5 . De rest blijft hetzelfde.
f ( x) = −25 + 15 sin 101 π( x − 5)
off
bladzijde 80
b
Om ongeveer op hetzelfde puntenaantal uit te komen zal er bij het kogelstoten dus
met een groter getal moeten worden vermenigvuldigd. Formule A hoort dus bij het
kogelstoten en formule B bij het speerwerpen.
Er moet gelden 15, 9803(d − 3, 80)1,04 = 800 .
Met algebra: (d − 3, 80)1,04 = 800
15, 9803
dh
27a
= 1 en a = 2 − 1 = 1 .
Voor de tweede grafiek geldt g ( x) = d + a sin b( x − c) met d = 600 + −100 = 250 en
2
2π
1
a = 600 − 250 = 350 . De periode is 52 dus b = 52 = 26 π en de grafiek start bij x = −13
dus c = −13 .
g ( x) = 250 + 350 sin 261 π( x + 13)
3.5 Gemengde opdrachten
0+2
2
ev
25
Ui
tg
er
sb
v
Hoofdstuk 3 - Transformaties
1

 1,04
d − 3, 80 =  800 
 15, 9803 
1
c
(
or
)
No

 1,04
d =  800  + 3, 80 ≈ 46, 87
 15, 9803 
Je kunt de vergelijking natuurlijk ook met de grafische rekenmachine oplossen.
Je moet dus minstens 46,87 meter gooien.
1,04
800
Of: c ⋅ 45 − 3, 80
= 800 geeft c =
≈ 16, 7339
1,04
45 − 3, 80
1,04
dus A = 16, 7339 ⋅ d − 3, 80
(
(
)
(
)
of: 15, 9803 ⋅ 45 − 3.80 = 800 geeft 41, 2 c =

 log 50, 0616
c = 41,2 log  800  =
≈~ 1, 05
 15, 9803 
log 41, 2
(
)
A = 15, 9803 ( d − 1, 93)
of: 15, 9803 ⋅ 45 − c
©
(
dus A = 15, 9803 ⋅ d − 3, 80
1,04
)
00
dus
15, 9803
)
1,05
1,04
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 67
1

 1,04
= 800 geeft 45 − c =  800  dus c ≈ 45 − 43, 07 = 1, 93 dus
 15, 9803 
© Noordhoff Uitgevers bv
⁄
67
31-03-2008 10:58:9
28a
b
c
d
e
f
c(0) = 10 mg/liter en c(8) = 10 ⋅ 0, 8 8 ≈ 1, 68 mg/liter.
Na de eerste herhaling is de concentratie 1, 68 + 10 = 11, 68 mg/liter.
Voor 16 < t < 24 geldt C = 10 ⋅ 0, 8 t + 10 ⋅ 0, 8 t − 8 + 10 ⋅ 0, 8 t −16 .
De concentratie blijft steeds toenemen.
Dan moet men steeds na 8 uur 10 − 1, 68 = 8, 32 mg/liter inspuiten.
Als de eerste injectie nog 10 mg/liter is geldt C = 10 ⋅ 0, 8 t . Als C = 1 mag men er weer
9 inspuiten. 10 ⋅ 0, 8 t = 1 geeft
log 101
0, 8 t = 101 dus t =
≈ 10, 32 .
log 0, 8
Er moet steeds minimaal 10 uur en 0, 32 × 60 ≈ 20 minuten tussen de injecties zitten.
( )
ev
er
sb
v
Hoofdstuk 3 - Transformaties
29a
b
c
Er geldt dan d = 81 − 165 = 8 en a = 181 − 8 = 173 .
2
De periode is 12 uur en 10 minuten ofwel 12 16 uur. Dus b = 2 π1 ≈ 0, 52 .
12 6
c = 4 23 − 14 × 12 16 = 1 85 dus W (t ) = 8 + 173 sin 0, 52(t − 1 85 )
In werkelijkheid is de stijging sneller dan bij de gevonden benadering terwijl de
afname van het tij aardig overeenkomt.
De gemiddelde top ligt op 34,5 cm. Het dal ligt op –55 cm.
34, 5 − 55
≈ −10, 25 en
2
a = 34, 5 + 10, 35 = 44, 75 .
De periode is weer 12 uur en 10 minuten dus b ≈ 0, 52 . c = 6 43 − 14 ⋅ 12 16 = 3 17
≈ 3, 71 .
24
W (t ) = −10, 25 + 44, 75 sin 0, 52(t − 3, 71)
De laatste grafiek lijkt veel meer een sinusoïde. De amplitude bij de eerste grafiek is
veel groter dus een veel groter verschil tussen hoog en laag water. De periode komt
overeen.
Er geldt dan d =
dh
d
Ga weer uit van W (t ) = d + a sin b(t − c) .
De gemiddelde top ligt op 181 cm. Het gemiddelde dal op –165 cm.
off
Ui
tg
bladzijde 81
or
ICT Grafieken verschuiven
bladzijde 82
⁄
68
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
©
No
A: f ( x) = x 3 heeft domein  ; bereik  ; snijpunten met de assen (0, 0); stijgt op 
B: f ( x) = 1 heeft domein 〈←, 0〉 ∪ 〈0, →〉; bereik 〈←, 0〉 ∪ 〈0, →〉; heeft geen
x
snijpunten met de assen; verticale asymptoot y-as; horizontale asymptoot de x-as;
daalt op het domein.
C: f ( x) = 2 x heeft domein  ; bereik 〈0, →〉; snijpunt met y-as (0, 1); horizontale
asymptoot x-as; stijgt op het hele domein.
D: f ( x) = 3 log x heeft domein 〈0, →〉; bereik  ; snijpunt met de x-as (1, 0); verticale
asymptoot y-as; stijgt op het hele domein.
E: f ( x) = x 4 heeft domein  ; bereik [0, →〉; snijpunt met x-as en y-as is (0, 0);
top (0, 0). De grafiek daalt op
〈←, 0〉 en stijgt op 〈0, →〉.
I_1
MW9_havobb_wiskb_2_1-Uitw.indd 68
© Noordhoff Uitgevers bv
31-03-2008 10:58:17
b
I_3a
b
c
d
I_4a
b
c
d
I_5
ev
Open het bestand dat hoort bij opdracht 2.
y = − f ( x) betekent dat de grafiek gespiegeld wordt in de x-as. Het veranderen in
y = f (− x) betekent dat de grafiek gespiegeld wordt in de y-as.
Bij sommige functies heeft het veranderen in y = f (− x) geen zichtbaar effect omdat
deze grafieken al symmetrisch zijn in de y-as. Bij het spiegelen valt het beeld dan
over het origineel. Geen enkele grafiek is symmetrisch in de x-as.
Ui
tg
I_2a
g ( x) = x 2 + 2
g ( x) = x 2 − 3
De formule van de nieuwe parabool ontstaat door bij de functie f 2 op te tellen,
respectievelijk 3 af te trekken.
Het resultaat is een verschuiving van 1 naar beneden. Dus g ( x) = x 2 − 1 .
f ( x) = ( x − 2)2 = ( x − 2)( x − 2) = x 2 − 2 x − 2 x + 4 = x 2 − 4 x + 4
De standaardparabool heeft top (0, 0). De nieuwe parabool heeft top (2, 0).
f (2) = (2 − 2)2 = 0 2 = 0 klopt; f (2) = 2 2 − 4 ⋅ 2 + 4 = 4 − 8 + 4 = 0 klopt.
f ( x) = ( x + 3)2 = ( x + 3)( x + 3) = x 2 + 3 x + 3 x + 9 = x 2 + 6 x + 9 . De top van de nieuwe
parabool is (–3, 0); f (−3) = (−3 + 3)2 = 0 2 = 0 ; f (−3) = (−3)2 + 6 ⋅ −3 + 9 = 9 − 18 + 9 = 0
. Beide controles kloppen.
De notatie met haakjes is het handigst, omdat je dan eenvoudig de top kunt
ontdekken.
off
F: f ( x) = sin x heeft domein  ; het bereik is [ −1, 1] ; de x-as wordt gesneden in
de punten (0 + kπ, 0) waarbij k een geheel getal is; de y-as wordt gesneden in
het punt (0, 0); de functie is periodiek met periode 2π ; f stijgt op de intervallen
⟨− 12 π + 2 kπ, 12 π + 2 kπ ⟩ en daalt op de intervallen ⟨ 12 π + 2 kπ, 1 12 π + 2 kπ ⟩
G: f ( x) = x heeft domein [0, →〉 en bereik [0, →〉; het randpunt is (0, 0);
f stijgt op het hele domein.
De nieuwe parabool heeft de formule g ( x) = ( x − 3)2 + 2 .
bladzijde 83
b
c
d
I_7
I_8a
b
c
-
De standaardfunctie g ( x) = x is 1 naar rechts geschoven.
De standaardfunctie g ( x) = x is 1 naar beneden geschoven.
De standaardfunctie h( x) = x 3 is 2 naar links geschoven.
©
or
De parameter c geeft de horizontale verschuiving van de standaardgrafiek aan.
Wanneer c > 0 dan is er sprake van een verschuiving naar rechts en wanneer c < 0
dan is er sprake van een verschuiving naar links. De parameter d bepaalt de verticale
verschuiving van de standaardgrafiek, d > 0 is een verschuiving omhoog, d < 0 een
verschuiving naar beneden.
Neem c = 2 ; het functievoorschrift wordt y = ( x − 2)3 .
Neem d = −2 ; het nieuwe functievoorschrift wordt y = 3x − 2 .
Het functievoorschrift wordt: y = sin( x + 2) + 1 .
No
I_6a
dh
er
sb
v
Hoofdstuk 3 - Transformaties
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 69
© Noordhoff Uitgevers bv
⁄
69
31-03-2008 10:58:25
d
e
f
I_9
De standaardfunctie f ( x) = sin x is 3 naar beneden geschoven.
De standaardfunctie f ( x) = sin x is 2 naar rechts geschoven.
De standaardfunctie g ( x) = 2 log x is 3 omhoog geschoven.
1 − 3.
x−2
De volgorde waarop je dit doet maakt geen verschil.
De verschoven grafiek heeft als voorschrift: f ( x) =
ev
ICT Grafieken vervormen
bladzijde 84
c
I_11a
b
c
d
I_12a
b
c
d
e
f
I_13
Ui
tg
Bij een waarde van a die groter is dan 1 wordt de grafiek verticaal uitgerekt. a > 1
Bij een waarde van a tussen 0 en 1 wordt de grafiek verticaal ingekrompen. 0 < a < 1
Wanneer a negatief wordt dan wordt de grafiek gespiegeld in de x-as en uitgerekt of
ingekrompen. Bij de waarde a = –1 wordt de standaardgrafiek alleen gespiegeld in de
x-as.
Alle functiewaarden worden met a vermenigvuldigd, vandaar dat deze transformatie
ook vermenigvuldiging ten opzichte van de x-as genoemd wordt.
off
b
De standaardfunctie g ( x) = sin x is met factor –3 vermenigvuldigd.
De standaardfunctie f ( x) = 1 is met factor 3 vermenigvuldigd.
x
De standaardfunctie g ( x) = 2 log x is vermenigvuldigd met factor 3.
De standaardfunctie h( x) = x 3 is met factor 1,7 vermenigvuldigd.
De standaardfunctie f ( x) = 2 x is met factor 40 vermenigvuldigd want
10 ⋅ 2 x+ 2 = 10 ⋅ 2 2 ⋅ 2 x = 40 ⋅ 2 x .
De standaardfunctie g ( x) = x 2 is met factor –3 vermenigvuldigd.
dh
y = 2 x2
y = −3 x 2
De nieuwe parabool ontstaat door de standaard parabool verticaal te
vermenigvuldigen met 2 respectievelijk met –3.
-
or
I_10a
er
sb
v
Hoofdstuk 3 - Transformaties
I_14a
b
c
d
Waarden van b tussen 0 en 1 rekken de grafiek van sin x horizontaal uit. 0 < b < 1
Waarden van b groter dan 1 laten de grafiek inkrimpen in de richting van de y-as.
b>1
Wanneer b negatief is wordt de grafiek eerst gespiegeld in de y-as en vervolgens
horizontaal ingekrompen of uitgerekt. b = –1 heeft alleen een spiegeling in de y-as tot
gevolg.
De x-waarden worden met een factor vermenigvuldigd, vandaar dat deze
transformatie ook wel vermenigvuldiging ten opzichte van de y-as wordt genoemd.
©
No
bladzijde 85
⁄
70
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 70
© Noordhoff Uitgevers bv
31-03-2008 10:58:29
I_15a
g ( x) = 2( 13 x)5 + 3 = 2 ⋅ ( 13 )5 x 5 + 3 =
b
h( x) =
c
3 =9
( 13 x) x
f ( x) = − sin( 13 x)
d
m( x) = 2 log( 13 x) = 2 log( 13 ) + 2 log x
e
f
2
243
er
sb
v
Hoofdstuk 3 - Transformaties
x5 + 3
x = 1+ x
3
1
1
x
k ( x) = 3 3 − 4 = 3 3 ⋅ 3 x − 4 = 3 3 ⋅ 3 x − 4
n( x) = 1 +
ev
1
3
-
I_17a
Vermenigvuldigen met factor 161 ten opzichte van de y-as geeft f ( x) = 16 x .
f ( x) = 16 x = 16 ⋅ x = 4 x . De grafiek kan dus ook door een verticale
vermenigvuldiging met factor 4 ontstaan uit de standaardgrafiek.
Ja. f ( x) = ax ontstaat door een horizontale vermenigvuldiging ten opzichte
van de y-as met factor 1a . Omdat f ( x) = ax = a ⋅ x ontstaat f ook uit de
standaardgrafiek door een verticale vermenigvuldiging met factor a , met a > 0 .
b
c
ICT Transformaties combineren
b
c
I_19a
b
c
f ( x) = 3( x − 1)2
f ( x) = 3( x − 1)2
Ja.
f ( x) = ( 13 x − 1)2 = 19 ( x − 3)2 de afleiding staat op bladzijde 86 van het boek bij de
grafiek.
f ( x) = ( 13 ( x − 1))2 = 19 ( x − 1)2
Verschuiven 1 naar rechts: g ( x) = x 2 wordt h( x) = g ( x − 1) = ( x − 1)2 vervolgens
horizontaal vermenigvuldigen met 3:
dh
I_18a
off
bladzijde 86
Ui
tg
I_16
2


h( x) = ( x − 1)2 → f ( x) = h( 13 x) = (( 13 x) − 1)2 =  x − 3  =
 3 
d
Horizontaal vermenigvuldigen met 3: g ( x) = x 2 wordt h( x) = g ( 13 x) = ( 13 x)2 = 19 x 2 .
Verschuiven 1 naar rechts: f ( x) = h( x − 1) = 19 ( x − 1)2 .
I_20a
f ( x) = 19 x 2 + 1
f ( x) = 19 x 2 + 1
Verschuiven 1 naar boven: g ( x) = x 2 wordt h( x) = g ( x) + 1 = x 2 + 1 . Vervolgens
horizontaal met 3 vermenigvuldigen: f ( x) = g ( 13 x) = ( 13 x)2 + 1 = 19 x 2 + 1
Horizontaal vermenigvuldigen met 3: g ( x) = x 2 wordt h( x) = g ( 13 x) = ( 13 x)2 = 19 x 2 .
Vervolgens 1 omhoog schuiven: f ( x) = g ( x) + 1 = 19 x 2 + 1 .
c
I_21a
b
f ( x) = 3 x 2 + 3
f ( x) = 3 x 2 + 1
©
2
or
b
( x − 3)
No
1
9
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 71
© Noordhoff Uitgevers bv
⁄
71
31-03-2008 10:58:37
c
I_22
Verschuiven 1 omhoog: g ( x) = x 2 wordt h( x) = g ( x) + 1 = x 2 + 1 . Vervolgens verticaal
met 3 vermenigvuldigen: f ( x) = 3 ⋅ h( x) = 3( x 2 + 1) = 3 x 2 + 3 .
Verticaal vermenigvuldigen met factor 3: g ( x) = x 2 wordt h( x) = 3 ⋅ g ( x) = 3 x 2 .
Vervolgens 1 omhoog schuiven: f ( x) = h( x) + 1 = 3 x 2 + 1 .
A: De grafiek van 2 log x wordt eerst horizontaal met 5 vermenigvuldigd en
vervolgens 3 naar rechts geschoven.
B: De grafiek van 2 log x wordt eerst horizontaal 3 naar rechts geschoven en
vervolgens horizontaal met 5 vermenigvuldigd want y = 2 log( 15 x − 3) .
C: De grafiek van 2 log x wordt eerst horizontaal vermenigvuldigd met factor 5 en
vervolgens 3 naar beneden geschoven (hierbij kun je de volgorde ook verwisselen).
ev
er
sb
v
Hoofdstuk 3 - Transformaties
I_24a
b
c
d
off
De parameter a bepaalt de amplitude van de grafiek. Wanneer a > 0 wordt de
standaardgrafiek niet gespiegeld in de x-as, wanneer a < 0 wordt de standaardgrafiek
ook nog gespiegeld in de x-as.
De parameter b heeft invloed op de periode. Wanneer 0 < b < 1 wordt de periode
groter, b > 1 heeft een kortere periode tot gevolg.
Parameter c bepaalt een horizontale verschuiving. c > 0 een verschuiving naar rechts,
c < 0 een verschuiving naar links.
Parameter d tenslotte zorgt voor een verticale verschuiving van de standaardgrafiek.
d > 0 is een verschuiving naar beneden.
Het maximum is 20 en het minimum is –10.
De evenwichtslijn ligt precies tussen het maximum en het minimum dus is de lijn
y=5.
De amplitude is 15.
De sinusgolf begint in het punt (60, 5).
dh
I_23
Ui
tg
bladzijde 87
-
I_26
f ( x) = sin 2 x + 1
I_27
g ( x) = d + a sin b( x − c) ;
evenwichtsstand y = 600 − 100 = 250 dus d = 250 ; maximum is 600 dan is a = 350
2
periode is 52 dan is b = 252π = 261 π ; startpunt (–13, 250), de verschuiving 13 naar links
dus c = −13 .
g ( x) = 250 + 350 sin 261 π( x + 13)
©
No
or
I_25
⁄
72
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 72
© Noordhoff Uitgevers bv
31-03-2008 10:58:43
er
sb
v
Hoofdstuk 3 - Transformaties
Test jezelf
bladzijde 90
b
c
d
Punt (0, 0) komt zo op (–4, 2) terecht.
(–1+4, –25–2) dus P(3, –27)
g ( x ) = ( x + 4 )2 + 2
De y-coördinaat op de grafiek van f is dan −6 − 2 = −8 dus moet gelden − x 3 = −8 wat
betekent dat x = 2 dus punt (2, –8).
ev
T-1a
b
Punt (1, –1) komt zo op (2, –3) terecht.
( −42 , 243 ) dus P(–2, 8)
c
g ( x) = −( 12 x)3 ⋅ 3 = −3( 12 x)3 = − 83 x 3
d
De y-coördinaat op de grafiek van f is dan −6 : 3 = −2 dus moet gelden − x 3 = −2 wat
betekent dan x = 3 2 dus punt ( 3 2 , −2)
T-3a
De standaardgrafiek van f ( x) = 2 log x 2 naar links en 2 naar boven schuiven.
De standaardgrafiek van g ( x) = x 2 eerst 4 naar links schuiven, vervolgens verticaal
vermenigvuldigen met 0,2 en dan 4 naar beneden schuiven.
De standaardgrafiek van h( x) = 1 6 naar rechts schuiven, vervolgens verticaal met 5
x
vermenigvuldigen en dan 7 naar boven schuiven.
De standaardgrafiek van j( x) = 2 x horizontaal vermenigvuldigen met 10.
c
d
T-4ab
Ui
tg
b
)
y = −2 is de evenwichtslijn dus d = −2 met a = 3 . De periode is 10 dus b = 2 π = 15 π
10
en de grafiek gaat door (6, –2) dus c = 6 .
Het functievoorschrift is dus f ( x) = −2 + 3 sin( 15 π( x − 6)) .
De transformaties zijn dan achtereenvolgens: verticaal vermenigvuldigen met 3,
horizontaal vermenigvuldigen met 5 , 6 naar rechts en 2 naar beneden schuiven.
π
off
(
bladzijde 91
b
Verticaal vermenigvuldigen met –3 en dan 4 naar links en 6 naar boven schuiven.
g ( x) = −3 x + 4 + 6
or
T-5a
dh
T-2a
©
No
T-6a
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 73
© Noordhoff Uitgevers bv
⁄
73
31-03-2008 10:58:49
c
T-7
T-8a
b
17+ 2
2
= 9, 5 met een amplitude
De periode is 12 maanden dus b = 2 π = 16 π .
12
Op t = 4 gaat de grafiek door de evenwichtsstand dus c = 4.
Hieruit volgt f (t ) = 9, 5 + 7, 5 sin( 16 π(t − 4)) .
Bereken met de grafische rekenmachine wanneer D = 5.
Dit geeft t ≈ 155, 7 en t ≈ 226, 8 .
De temperatuur was dus van dag 156 tot en met dag 226 boven de 5 °C dus
gedurende 71 dagen.
Ga uit van f (t ) = d + a sin b(t − c) .
Het maximum is 58 en het minimum –78 dus d =
57− 78
2
= −10 met a = 58 − −10 = 68 .
De periode is 12 uur en 20 minuten dus b = 2 π1 ≈ 0, 51 .
12 3
Het minimum is om 4.10 uur en het maximum om 10.14 uur. De grafiek gaat dus om
4.10 + 10.14 = 7.12 uur door de evenwichtsstand dus c = 7, 20 .
2
Dus f (t ) = −10 + 68 sin(0, 51(t − 7, 20)) .
Verticaal vermenigvuldigen met –1 komt neer op spiegelen in de x-as.
Horizontaal vermenigvuldigen met –1 komt neer op spiegelen in de y-as.
Horizontaal vermenigvuldigen met 3 of –3 geeft hetzelfde resultaat.
©
No
or
dh
off
Ga uit van f ( x) = d + a sin b(t − c) .
Het maximum is 17 en het minimum 2 dus d =
a = 17 − 9, 5 = 7, 5 .
ev
b
Ui
tg
er
sb
v
Hoofdstuk 3 - Transformaties
⁄
74
Moderne wiskunde 9e editie uitwerkingen havo B deel 2
MW9_havobb_wiskb_2_1-Uitw.indd 74
© Noordhoff Uitgevers bv
31-03-2008 10:58:53