PowerPoint-presentatie

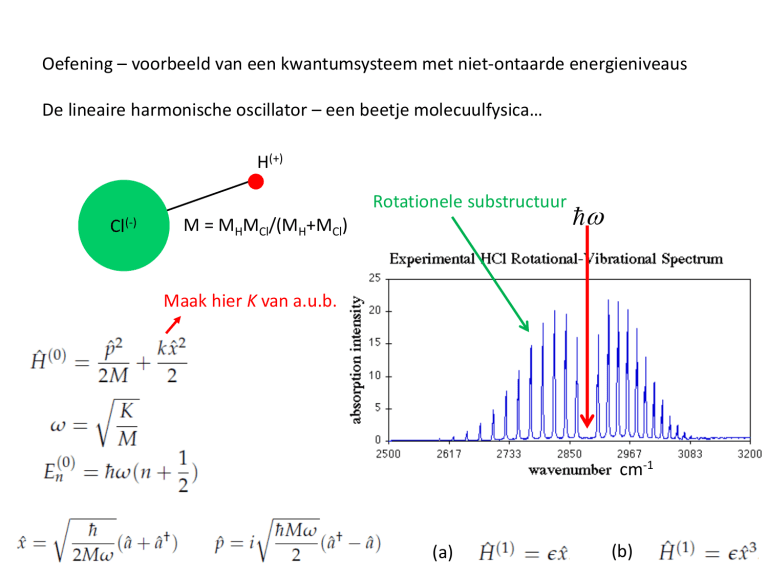
Oefening – voorbeeld van een kwantumsysteem met niet-ontaarde energieniveaus
De lineaire harmonische oscillator – een beetje molecuulfysica…
H(+)
Rotationele substructuur
Cl(-)
M = MHMCl/(MH+MCl)

Maak hier K van a.u.b.
cm-1
(a)
(b)
Inleiding tot de Atoom- en Molecuulfysica
Hoofdstuk 4 - Benaderingstechnieken
Maak hier K van a.u.b.
Niet-ontaarde stationaire storingsrekening
 xˆ n  
â

2M

 â  n  
(a)
 n 1 n 1  n n 

2M 

 n 1 n 1  n n 
n  n 

 2M 
c
1
2
1 2


E  n  
n 1  n    n   
2
2  2M
2  2K


c
n
Opmerkingen :
1. De grondtoestand van de H.O. met n=0 verdient in principe een aparte aanpak.
Bemerk echter dat, aangezien â|0> = 0, dit geval ook voldoet aan de afgeleide
formules.
2. De perturbatie genereert geen diagonaal-matrixelementen in de basis van de
ongestoorde Hamiltoniaan. Gevolg : er is geen eerste orde energiecorrectie. De
laagste orde energiecorrectie is kwadratisch in .
3. Voor deze storing levert tweede orde storingsrekening een exact resultaat voor de
energiecorrectie. Dit is een gevolg van het feit dat de energiecorrectie ook echt
kwadratisch is in . We kunnen dit als volgt inzien: de Hamiltoniaan van het systeem
kan worden herschreven als:
Ĥ  0
 E1 0
















 Ĥ 1
Niet diagonaal in deze basis
Niet-0 matrix-elementen in blokken met zelfde En(0)
E1 0
E 20
E 20
E 20
E 30
E 30
E 30
E 30















 0 
E3 
Oplossing : éérst diagonaliseren binnen blokken met zelfde En(0)
Daarna reeds gekende formules toepassen
Inleiding tot de Atoom- en Molecuulfysica
Hoofdstuk 4 - Benaderingstechnieken
Ontaarde stationaire storingsrekening: voorbeeld Stark effect op H-atoom
Ongestoord systeem : niet-relativistisch waterstofatoom
Enlm
nlm
zie hoofdstuk 1, blz. 25
Storing
Bereken effect op n = 2 niveau
Bereken effect op n =1 niveau
Effect op de n = 2 naar n = 1 transitie ?
Correctie !
Inleiding tot de Atoom- en Molecuulfysica
Hoofdstuk 4 - Benaderingstechnieken
Tijdsafhankelijke storingsrekening (in deze cursus) : waarschijnlijkheden van overgangen
tussen energieniveaus waarbij elektromagnetische straling wordt geabsorbeerd of
ˆ 1 t  Hˆ cos  t
uitgezonden. De storings-Hamiltoniaan is tijdsafhankelijk : H
pert
if

if  E f  Ei
met Hpert een elektromagnetische multipooloperator en
Voor i en f discrete energieniveaus : initiële overgangswaarschijnlijkheid (t heel klein)
Pi f  t  
f
Hˆ pert  i
2
2
t2
Voor i een welbepaalde begintoestand en f behorend tot een continuüm aan
energiniveaus (band) (Fermi’s Gulden Regel)
Wi f 
dPi f
dt

2
f
Hˆ pert  i
2
 Ef 
Meer details (concrete berekening)  Kwantummechanica II
Inleiding tot de Atoom- en Molecuulfysica
Hoofdstuk 4 - Benaderingstechnieken
Ontaarde stationaire storingsrekening: voorbeeld Stark effect op H-atoom
2p1 , 2p  1
1
 2s0  2p0
2
1
 2s0  2p0
2


E // aangelegd elektrisch veld (z-richting)
E ^ aangelegd elektrisch veld (x, y richting)