Lenzen
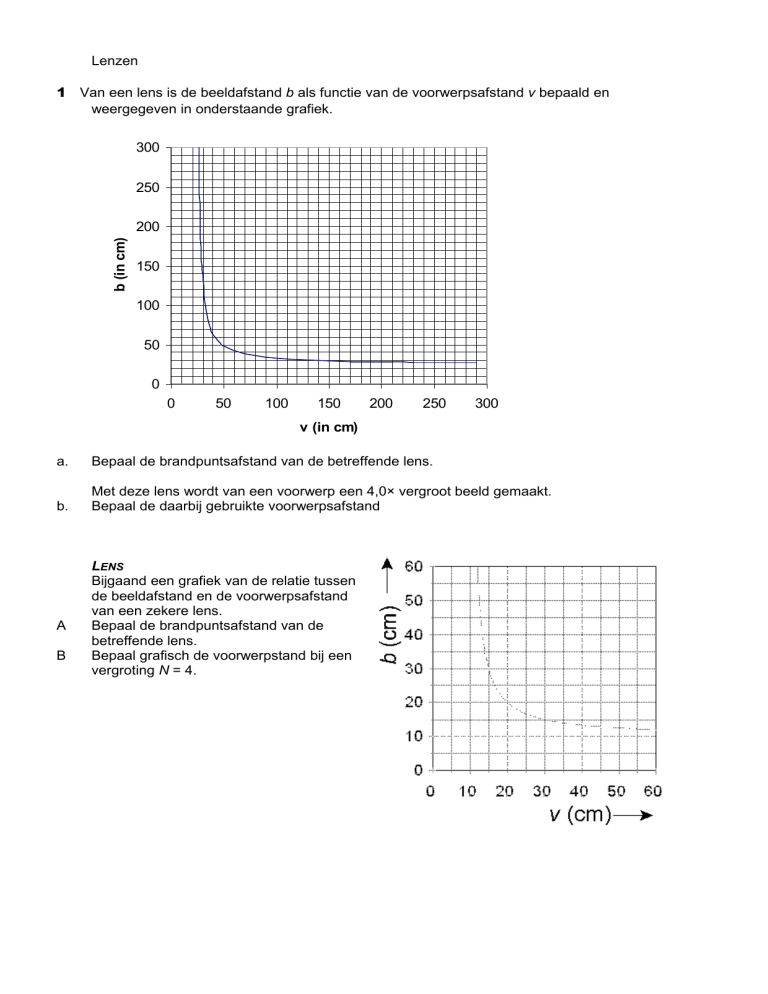
1 Van een lens is de beeldafstand b als functie van de voorwerpsafstand v bepaald en
weergegeven in onderstaande grafiek.
300
250
b (in cm)
200
150
100
50
0
0
50
100
150
200
250
300
v (in cm)
a.
Bepaal de brandpuntsafstand van de betreffende lens.
b.
Met deze lens wordt van een voorwerp een 4,0× vergroot beeld gemaakt.
Bepaal de daarbij gebruikte voorwerpsafstand
A
B
LENS
Bijgaand een grafiek van de relatie tussen
de beeldafstand en de voorwerpsafstand
van een zekere lens.
Bepaal de brandpuntsafstand van de
betreffende lens.
Bepaal grafisch de voorwerpstand bij een
vergroting N = 4.
A
B
A
B
LENS
Bijgaand een grafiek van de relatie
tussen de beeldafstand en de
voorwerpsafstand van een lens.
Bepaal de brandpuntsafstand van de
betreffende lens.
Bepaal met behulp van de grafiek de
vergroting als voorwerp en beeld 80
cm van elkaar verwijderd zijn.
Teken daartoe de lijn v + b = 80.
Uitwerking
Een punt van de grafiek is het punt
v = 16 cm, b = 40 cm.
Toepassing lenzenformule: f = 11,4 cm.
Teken de lijn. De snijpunten geven de
mogelijkheden waar een scherp beeld
gevormd met deze lens.
b 67
5,2
v 13
, maar ook
b 13
N
0,19
v 67
.
N
2
CONSTRUCTIE
Van een punt L gaat een lichtstraal door de lens naar O. Zie figuur. In de figuur zijn ook de
hoofdas en een brandpunt aangegeven.
Construeer de straal van L naar O.
Uitwerking
Construeer eerst het beeld van L en bedenk dan dat alle stralen vanuit L die op de lens
vallen via dat punt moeten, dus ook de straal naar O.
3
Constructie
Construeer het verloop van de getekende straal via de lens.
Uitwerking
Taktiek 1: De getekende straal beschouw als een uit een bundel evenwijdige stralen.
Evenwijdige stralen zullen elkaar op brandpuntsafstand snijden.
Een bundel evenwijdig aan de hoofdas in het hoofdbrandpunt F en een bundel evenwijdig
aan een bijas in het bijbrandpunt F’.
Taktiek 2: Doe net of een punt van de getekende straal een voorwerp is en construeer het
beeld van dat voorwerp met behulp van de constructiestralen. Alle stralen, dus ook de reeds
getekende, moet door het beeld.
4
CONSTRUCTIE
Construeer de straal van L via lens naar O.
Uitwerking:
Construeer eerst het beeld van L en trek de straal van dat beeld naar O.
5
OOG
Mijn oog kan accommoderen van 30 cm tot 92 cm. Ik zet een bril met glazen van +2 dpt
Bereken de grootste afstand waarop ik een voorwerp met die bril scherp kan zien.
6
BIJZIENDE
Een bijziende heeft een nabijheidspunt op 18 cm en een vertepunt op 0,50 m van zijn
ooglens.
Hij zet een bril op van +1 dpt.
Bereken waar zijn nabijheidspunt en vertepunt met bril liggen.
BEELD VAN TL-BALK OP TAFEL
In een lokaal wil men met een lens met een sterkte van 5 dioptrie een afbeelding van de TLbalk op de tafel maken. De TL-balk hangt 2,50 m boven de tafel.
Bereken/Bepaal waar men de lens moet houden.
Uitwerking
Berekening:
5 dioptrie betekent ƒ = 0,20 m = 20 cm en dus
1 1 1
1 1
1
v b
f
v b 20
Bovendien volgt uit het verhaal dat b + v = 250.
Daarmee heb je twee vergelijkingen met twee onbekenden.
Natuurkundig is de zaak daarmee opgelost. De kunst is nu het rekenwerk.
Bepaling
Deze vraag is dezelfde als bij opgave 1, maar dan grafisch.
Teken de grafiek van b als functie van v.
300
250
200
b (in cm)
7
150
100
50
0
0
50
100
150
200
250
300
v (in cm)
Trek de lijn met als vergelijking: b + v = 250
De b,v-grafiek van de lens is al getekend.
Als aan beide is voldaan, dus op de snijpunten, dan voldoe je aan alle eisen. Er zijn dus twee
oplossingen. De vergroting vind je uit b/v.
8
a
b
SCHERPTEDIEPTE
Om de scherptediepte te vergroten wordt de diameter van de pupil gehalveerd door de
lichtintensiteit te vergroten..
Leg met een tekening uit dat daardoor de scherptediepte wordt vergroot.
Met welke factor moet men de lichtsterkte opvoeren om toch dezelfde helderheid op het
netvlies te krijgen?
Uitwerking vraag b.
We beschouwen de pupil als een cirkel met als oppervlakte r².
Als je de diameter en dus ook de straal halveert, wordt de oppervlakte 4 keer zo klein
vanwege dat kwadraat. Wil je evenveel licht, dan zul je de lichtsterkte vier keer zo groot
moeten maken.
9
Met een lens (f = + 40 cm) wil men een beeld maken op een scherm. Het beeld mag maar
half zo groot zijn als het 50 cm grote voorwerp .
Bereken waar het voorwerp en de lens geplaatst moeten worden.
Uitwerking:
1 1 1
v b f
b
1
N
v
2
10
1 1 1
v b 40 1 1 1
b 60 v 120 cm
2b b 40
b
v 2b
v
Stralengang
Getekend zijn een lens met zijn brandpunt F, een voorwerp L en een schermpje P
Construeer de bundel die vanuit L het schermpje verlicht.
11
Oog
Een normale waarde voor de diameter van een oog, dat we gemakshalve maar als een bol
beschouwen, is 17 mm. Op 20 cm voor dat oog bevindt zich een letter k, die 3,0 mm hoog is.
De letter wordt scherp gezien.
Maak een beargumenteerde schatting van de sterkte van de ‘lens’ van het oog kijkend naar
die letter k.
12
Projector
Bijgaand zie je een tekening van een projector uit het boek.
Leg uit wat het effect op het beeld is, als we de condensorlens verwijderen uit de projector.
13
Lens
Een lamp beschijnt via een lens een scherm AB. Zie de tekening hieronder met lamp L,
lens, brandpunt F, scherm AB en hoofdas.
Construeer en arceer de bundel die het scherm belicht.
Uitwerking
Om de stralengang te kunnen tekenen moet je eerst het beeld van L construeren. Dit doe je
met twee constructiestralen. Vanuit L door het optisch midden van de lens. Die straal gaat
rechtdoor. Als tweede een straal evenwijdig aan de hoofdas; deze breekt door het brandpunt
F. Het snijpunt van de twee uittredende stralen is het beeld.
Je ziet dat er rechts van de lens geen snijpunt is. Je moet de stralen dus doorstippelen links
van de lens tot ze elkaar snijden. Zo vind je het virtuele beeldpunt B van lamp L.
Alle stralen die vanuit L vertrekken, lijken na breking uit B te komen. Zo ook de stralen die de
gevraagde bundel begrenzen. Je stippelt de lijnen vanuit B naar A en B; zodra ze de lens
passeren, kun je die lijnen gewoon trekken. Tenslotte trek je de lijnen vanuit L naar de
beginpunten van de gebroken stralen op de lens en arceer je het gebied ertussen. Dat is de
bundel.
Ter vergelijking kijk je bijv. naar Newton 1a, verwerkingsboek blz. 76, opgave 38 e/o 39.
14
Oog – scherptediepte
Leg uit hoe je bij het oog de scherptediepte kunt vergroten. Let op: de opdracht bestaat uit
twee delen. A. Hoe kun je de scherptediepte vergroten? en B. Leg uit waarom dat werkt.
Uitwerking:
De scherptediepte wordt vergroot door de pupil te verkleinen. De pupil is het diafragma van
het oog. Een kleiner diafragma vergroot de scherptediepte. Een onscherp beeld ontstaat
door de verkeerde plaats van het scherm. In het geval van het oog is dat het netvlies. In
plaats van een punt geeft ieder voorwerpspunt een vlekje. Als je die vlekjes kleiner maakt,
neemt de onscherpte af, dus diafragmeren.
15
Construeer de straal van L naar O in deze situatie:
Uitwerking:
Een voorwerpspunt op brandpuntsafstand geeft een evenwijdige bundel. Dat het een
evenwijdige bundel wordt, kun je ook vaststellen na zorgvuldige tekening in de
standaardprocedure. De procedure is om eerst het beeld van L te construeren. Daartoe geef
je eerst het brandpunt rechts van de lens aan.
16
Een oog met een nabijheidspunt op 40 cm van het oog krijgt een contactlens van 1,00
dpt. Bereken de kleinste afstand waarop het oog met contactlens nog scherp ziet.
Uitwerking
Het nabijheidspunt ligt op 40 cm. Dat betekent dat bij maximaal accommoderen het oog
scherp stelt op 40 cm ervoor. Ook als daar een lens tussen zit. Dan kijkt het ook naar het
virtuele beeld op 40 cm ervoor en is voor die lens b = 40 cm.
S = 1,00 dpt f = - 1,00 m
1 1 1
1
1
1
v 67 cm
v b f
v 40 100
17
Construeer het verdere verloop van de bundel die door het diafragma op de lens valt zoals
getekend.
Uitwerking:
Ook hier is de standaardprocedure: beeld van L construeren. Helaas ligt dat niet op het
papier. Je kunt er natuurlijk een blad aanplakken. Maar je kunt ook met de bij-assen en het
brandvlak werken. Teken dus voor elk van de bundel-begrenzende stralen een lijn
evenwijdig eraan door het optisch midden. Waar die het brandvlak snijdt, gaat ook de
oorspronkelijke straal heen.
18
LAMP
Van een lamp valt een bundel licht op een lens. Van die bundel zijn de twee stralen getekend
die de bundel begrenzen. Tevens is de positie van de lens, de hoofdas en het brandpunt
aangegeven. Zie figuur ….
Construeer het verloop van de bundel voorbij de lens.
19
OOG
Je bekijkt een voorwerp dat slechts 15 cm van je oog is verwijderd door een lens. De lens
maakt een beeld van dat voorwerp. Dat beeld bevindt zich 30 cm van je oog.
De afstand lens-oog is 2,0 cm
Bereken de sterkte van de gebruikte lens.
20
DIA
Een voorwerp op een dia is 20 mm groot en 12 mm breed. De dia bevindt zich 6,0 cm voor
een lens met een brandpuntsafstand van 55 mm. De lens zorgt voor een scherp beeld op
een scherm.
Bereken de oppervlakte van het voorwerp op het scherm.
21
LENSCONSTRUCTIE
Een puntvormige lamp L bevindt zich voor een positieve lens. Van twee stralen van de lamp
is getekend hoe ze uit de lens komen. Zie figuur 4 op het antwoordblad. Daarin is ook een
brandpunt van de lens en een punt P aangegeven.
Uitwerking:
Construeer in figuur 4 op het antwoordblad de straal die vanuit L via de lens naar punt P
gaat.
Door de twee getekende stralen door te trekken vind je het beeld B.
Alle stralen uit de lens komen daar vandaan, ook de straal door het optisch midden.
De straal evenwijdig aan de hoofdas moet uit F komen. Deze snijdt de straal door het optisch
midden in L.
Nu trek je naar P de straal vanuit B.
De komt in het begin uit L.
22
LENSBEREKENING
Met behulp van een lens met een brandpuntsafstand van 135 mm wordt van een 20 cm
groot voorwerp een foto gemaakt. Het beeld op het negatief blijkt 10 mm groot te zijn.
Bereken de afstand van het voorwerp tot de lens.
Uitwerking:
1 1 1
f
Lens met brandpuntsafstand 135 mm: v b
L
b
10
N B
LV v
200
L = 200 mm en L = 10 mm:
V
B
1 1
1
........(1)
v b 135
b
.........(2)
v
Je hebt nu twee vergelijkingen met de onbekenden b en v.
Oplossen hiervan levert v = 2,8 m
23
BIJZIENDE
Een bijziende heeft een nabijheidsafstand van 15 cm en een vertepunt op 75 cm. Hij zet een
bril op met een sterkte van 2 dioptrie.
Bereken of hij een voorwerp op 2,00 m afstand scherp kan zien.
Uitwerking:
De bijziende kan scherp zien wat zich bevindt tussen 15 en 75 cm van zijn oog.
Een voorwerp op 2,00 m voor de bril levert een beeld :
1 1 1
1
1
2 b 0,40 m
v b f
2,00 b
Het beeld, gevormd door de bril - en dat is waar het oog naar kijkt - bevindt zich 40 cm voor
het oog. Dat ligt binnen de marge 15-75 cm en kan de bijziende dus scherp zien.
SPIEGEL
Ter gelegenheid van dit proefwerk heeft iemand zijn nabijheidspunt zonder bril bepaald en
komt op 23 cm. Als bijziende moet hij een bril van 1,75 dpt dragen. Die heeft hij echter niet
op, als hij ‘s morgens vroeg in de spiegel kijkt.
Leid af op welke afstand hij van de spiegel moet staan, wil hij zichzelf scherp kunnen zien.
Uitwerking:
1
Uit de gegevens volgt dat het nabijheidspunt op 23 cm en het vertepunt op 1,75 = - 57 cm
ligt.
Dat betekent dat het voorwerp zich tussen de 23 cm en
57 cm moet bevinden om scherp gezien te worden.
Het voorwerp ligt even ver achter de spiegel als het
voorwerp ervoor.
Dus de ogen moeten zich minimaal 23:2 = 11,5 cm van de
spiegel vandaan bevinden en maximaal 57:2 = 28,5 cm.
24
A
B
LENS MET KAARS
Op een statief staat een lens met een brandpuntsafstand van 20 cm. Een kaars staat 1,00 m
achter de lens.
Bereken de vergroting van het door de lens gevormde beeld.
In een verder grote lege ruimte bevindt zich op één lijn: kaars - lens - mijn oog. Ik kijk door de
lens naar de kaars. De lens en de kaars staan nog op dezelfde plaats.
Mijn nabijheidspuntafstand is 30 cm en mijn vertepunt ligt op 1,00 m.
Bereken waar ik moet gaan staan om dat beeld scherp te kunnen zien. Geef dat ook in een
schets weer.
Uitwerking:
A
1 1 1
1
1 1
b 25
v b f
100 b 20
B
Het beeld wordt gevormd
25 cm van de lens
vandaan. Ik moet daar
weer 30 cm vandaan gaan
staan om het beeld scherp
te kunnen waarnemen,
zodat ik tenminste 55 cm
van de lens moet staan.
Maar niet meer dan 1,25 m
vanwege het vertepunt.
N
b 25
0,25
v 100
N = 0,25
25
Constructie
BB’ is het beeld van voorwerp LL’, zoals dat gevormd wordt door een lens. De tekening is
gemaakt met als schaal 1:10.
Bepaal door constructie de positie van de lens.
Construeer de positie van het brandpunt.
26
Berekening
De afstand tussen een raam en de tegenoverliggende muur is 4,00 m.
Je beschikt over een lens met een brandpuntsafstand van 25 cm.
A
B
Bereken waar je de lens moet houden om een scherp beeld van het raam op de muur te
krijgen.
27
Normaal oog met bril
Iemand met een normaal oog heeft een nabijheidspuntafstand van 25 cm.
Hij zet een bril op met S = 1,00 D.
Bepaal op welke afstand van het oog een voorwerp moet staan als het scherp gezien moet
worden.
28
Bijziende
Ik ben bijziende en draag in de klas een voor mij geschikte bril met een sterkte van - 1,75
dioptrie.
Als ik zonder bril 50 cm voor een spiegel sta, kan ik mijzelf dan scherp zien in de spiegel?
Leid het antwoord op die vraag af.
Uitwerking:
Een bijziende heeft een bril om van voorwerpen die ‘oneindig’ ver weg zijn een beeld te
maken in het vertepunt. De evenwijdige bundel uit het oneindige lijkt dan te komen uit het
vertepunt, de lens is dan ‘plat’ en vormt met ongeaccommodeerd oog een scherp beeld. De
brandpuntsafstand van de geschikte negatieve lens is gelijk aan de afstand oog-vertepunt.
Zonder bril kan de bijziende scherp zien tot zijn vertepunt; in het gegeven geval dus tot 0,57
f
1
1
0,57 m
S 1,75
.
m. Immers
Als ik 50 cm voor de spiegel sta, staat mijn spiegelbeeld er 50 cm achter; dus 1,00 m van mij
vandaan. Ik kan het dus zonder bril niet scherp zien.
29
Loep
In een loep met een brandpuntsafstand van 2,5 cm zie ik een 4,00 maal vergroot beeld van
een stuk van mijn nagel.
Bereken de afstand tussen nagel en loep.
Uitwerking:
Als je door een loep naar een vergroot beeld kijkt, dan kijk je naar een virtueel beeld.
b
4 b 4v
v
1 1 1
1
1
1
v 1,875
v b f
v 4v 2,5
N
En dus is v = 1,9 cm
30
Kopie 1:1
Het blijkt dat een lens een beeld maakt van een voorwerp dat 40 cm voor een lens staat. Het
beeld is even groot als het voorwerp, namelijk 12 cm.
Bepaal de sterkte van de gebruikte lens.
Uitwerking:
1 1 1
1
1
S
5,0 dpt
v
b
f
0
,
40
0
,
40
N = 1 b = v = 0,40 m
LENS
Een positieve lens kan als een vergrootglas/loep werken.
Maak een constuctietekening waaruit dat blijkt.
Uitwerking:
Je maakt een van de onderstaande tekeningen van resp. een ‘vergrootglas’ en het juiste
gebruik van een loep.
DIGITALE CAMERA
In een aantal opzichten kun je een digitale camera vergelijken met een oog.
Zoals een oog ‘kegeltjes’ en ‘staafjes’ heeft als sensoren, heeft een digitale camera pixels.
Bij een bepaald type camera wordt het beeld opgebouwd uit 832 x 624 pixels.
Een oog heeft een netvlies, waarvan de rol bij zo’n camera wordt vervuld door een chip. De
832 pixels op de chip van deze digitale camera beslaan 5,8 mm. De lens van de camera
heeft een brandpuntsafstand van 7,0 mm; die van het oog is variabel.
Een oog heeft een scheidend vermogen van 0,5'.
1
A
B
Je weet natuurlijk dat 1 boogminuut = 1' = 60 graad.
Vergelijk het scheidend vermogen van deze camera met het scheidend vermogen van het
oog.
Met behulp van deze camera maak ik een scherpe foto van een 4,2 m hoge lantaarnpaal,
waar ik 10 m vandaan sta.
Bereken de grootte van het beeld van de lantaarnpaal op de chip.
Uitwerking:
Het gaat om hoeken. Teken dan die hoeken.
Er zitten 832 pixels op 5,8 mm.
De afstand tussen twee pixels is dus 6,97 m.
De hoek = 6,97106 / 7,00 mm = 1,00103 rad = 0,057 = 3,4'
Dat is 7 keer zo groot. Het scheidend vermogen van het oog is dus 7 keer zo klein.
De toren heeft v = en dus is b = 7,0 mm.
N = b/v = BB’ / LL’ 0,0070 / 10 = BB’ / 4,2 BB’ = 2,9 mm
BIJZIENDE
Als bijziende heb ik zonder bril wel problemen met kijken op afstand, maar lezen gaat zonder
bril prima.
Met bril gaat het kijken op afstand goed, maar het lezen geeft nu problemen.
Leg dat laatste uit aan de hand van de stralengang van het licht van een voorwerp door de
bril.
Uitwerking:
Een bijziende draagt een negatieve bril. Een negatieve lens maakt een verkleind virtueel
beeld. Tekenen! Dat beeld is te klein om te lezen. Of:
Als ik lees, houd ik het boek dichtbij. Het oog accommodeert maximaal. Als ik een negatieve
lens voor mijn oog houd wordt de bundel nog divergenter, het oog krijgt dat niet meer
geconvergeerd.
LENS
Een positieve lens kan een vergroot beeld maken van een voorwerp.
Maak een constructietekening waaruit dat blijkt. Geef de richting van de stralen aan.
DIGITALE CAMERA
De lens van de camera heeft een brandpuntsafstand van 7,0 mm. In plaats van een filmpje
zit er op die plaats een chip.
Met behulp van deze camera maak ik een scherpe foto van een 4,2 m hoge lantaarnpaal,
waar ik 10 m vandaan sta.
Bereken de grootte van het beeld van de lantaarnpaal op de chip.
OPTIMATE
Een optimate is een pincet met een ingebouwd lensje. Zie de figuren 2a en 2b. Figuur 2b
geeft een schematische doorsnede van de optimate weer.
Figuur 2a
figuur 2b
A
Het apparaatje is zo geconstrueerd dat een gebruiker een voorwerpje bij de pincetpunten
met een ongeaccommodeerd oog kan bekijken. In een horlogemakerij worden optimates
verstrekt aan alle medewerkers die zich met kleine onderdelen van horloges moeten
bezighouden.
Een jonge medewerker probeert de optimate even uit, maar kan de kleine onderdelen zonder
optimate even gedetailleerd zien.
Geef een reden waarom het voor deze medewerker toch zinvol is de optimate bij zijn werk te
gebruiken.
In figuur 3 is nogmaals een doorsnede van de optimate weergegeven, maar nu in combinatie
met het oog van een waarnemer. De lenzen van het oog en van de optimate zijn hierin
schematisch weergegeven. Daarin is een lichtstraal getekend vanuit V tot de ooglens.
Figuur3
B
De ooglens bevindt zich in ongeaccommodeerde toestand.
Construeer en arceer in figuur 3 de volledige lichtbundel die vanaf punt V op het netvlies van
het oog valt.
De kwaliteit van het lensje blijkt tegen te vallen. Zo worden de verschillende kleuren van een
witte lichtbundel verschillend gebroken. Dit verschijnsel heet chromatische aberratie. Het
wordt veroorzaakt doordat de brekingsindex van het glas afhangt van de golflengte van het
licht. De brekingsindex van het glas van het lensje is voor rood licht gelijk aan 1,514 en voor
blauw licht gelijk aan 1,524. Om de chromatische aberratie van de optimate te onderzoeken,
wordt op de hoofdas een puntvormige, witte lichtbron L voor het lensje geplaatst. Het licht
van verschillende kleuren vormt op verschillende afstanden van de lens een beeldpunt. Zie
figuur 4. In deze figuur zijn de randstralen van de bundels voor rood licht en blauw licht
weergegeven.
Figuur 4
C
A
Ergens in het gebied tussen P en Q wordt een wit scherm loodrecht op de optische as van
de lens gehouden. Er wordt een nagenoeg witte cirkelschijf met een roodachtige rand
waargenomen.
Leg uit of het scherm dichter bij P of dichter bij Q wordt gehouden.
Uitwerking:
In beide gevallen, dus zowel met als zonder optimate, ziet de jonge medewerker even
scherp en gedetailleerd. Alleen moet hij zonder optimate sterk accommoderen en dat is erg
vermoeiend.
Pas op: Als om een reden wordt gevraagd, wordt de eerste reden beoordeeld!!
B
Tussen optimate en oog lopen de stralen evenwijdig, alsof ze komen uit het
oneindige.
de straal door het midden van het oog gaat rechtdoor en waar die terecht komt,
komen alle stralen samen. Dat is eigen aan een scherp beeld.
De bundel wordt begrensd door het diafragma en is gearceerd getekend.
CAMERA
Met een camera, ƒ = 50 mm, wordt een 40 m van de fotograaf verwijderd gebouw
gefotografeerd van 28 m hoogte.
Bereken de grootte van het gebouw op het negatief.
Uitwerking:
v » f b f = 0,050 m
N
b BB'
0,050 BB'
BB' 0,035 m
v
LL'
40
28
CONSTRUCTIE
Vanuit een puntvormige lichtbron L valt licht op een positieve lens. Tegen deze lens staat
een diafragma met een cirkelvormig gat. Daardoor ontstaat op de wand een lichtvlek met
een diameter van 1,00 cm en wel 6,00 cm van het brandpunt vandaan. Getekend zijn de posities van de lichtvlek, lens, lichtbron en brandpunt.
A
Construeer de positie van het cirkelvormige gat.
De grootte van het cirkelvormige gat in je constructie opmeten is niet nauwkeurig.
B
Bereken de grootte van het gat in het diafragma.
OOG
Th.Pernot heeft ter gelegenheid van dit proefwerk zijn nabijheidspunt zonder bril bepaald en
komt op 23 cm. Als bijziende moet hij een bril van 1,75 dpt dragen, maar zijn reservebril
heeft een sterkte van 1,50 dpt.
Leid af op welke afstand hij met de reservebril scherp kan zien.
Variant: Leid af af of hij een voorwerp op 1,50 m met de reservebril scherp kan zien.
LOEP
Bij goed gebruik van de loep door een normaal ziend persoon wordt een voorwerp in het
brandpunt geplaatst. Uit de loep komt dan vanuit elk voorwerpspunt een evenwijdige bundel
en hoeft de gebruiker van de loep niet te accommoderen.
Th.Pernot heeft ter gelegenheid van dit proefwerk zijn nabijheidspunt bepaald en komt op
23 cm. Als bijziende zou hij een bril van 1,75 dpt moeten dragen.
Hij gebruikt een loep met een brandpuntsafstand van 2,50 cm en houdt deze 10,0 cm van
zijn oog.
Bereken waar hij het te bekijken voorwerp moet houden om zonder accommoderen ernaar te
kijken door de loep en het dan scherp te zien.
A
B
A
BEELD VAN LAMPJE
Bij de volgende opticavraag gaat het om een lampje en een schermpje op 1,00 m
daarvandaan.
Tussen beide plaats ik een lens. Het gloeidraadje in het lampje is 10 mm lang en evenwijdig
aan het scherm. Het blijkt dat ik een scherp beeld krijg, als de lens 11,3 cm van het scherm
verwijderd is.
Bereken de sterkte van de gebruikte lens.
Bepaal waar ik de lens ook kan plaatsen om een scherp beeld van het lampje op het scherm
te krijgen.
Uit de tekst volgt dat b = 11,3 cm en dat v = 100 - 11,3 = 88,7 cm, zodat
1 1 1
1
1
S
9,98
v b f
0,887 0,113
S = 9,98 dpt of S = 10 dpt.
B
In de lensvergelijking zijn de rol van v en b verwisselbaar. Dus ook v = 11,3 cm met
b = 88,7 cm is een oplossing.
1 1
9,98
Je kunt natuurlijk ook combineren v b
met v + b = 1,00 en gaan rekenen.
NABIJHEIDSAFSTAND
Je nabijheidsafstand is 20 cm en je vertepunt ligt op 100 cm. Je kijkt door een lens met een
brandpuntsafstand van 50 cm en ziet een omgekeerd beeld van wat zich in de verte afspeelt.
Leid af op welke afstand van de lens je je bevindt.
Antw: 70 cm - 150 cm
CONSTRUCTIE
Construeer de lichtstraal van A via de positieve lens met brandpunt F naar B. Zorg ervoor dat
de opeenvolgende stappen van de constructie te herkennen zijn.
A
B
C
FOTO
Je wilt een foto maken van een boom die 5,0 m hoog is.
De lens van de camera die je gebruikt heeft een brandpuntsafstand van 5,0 cm.
Je gaat 10 m van de boom staan.
Bereken de beeldafstand.
Bereken de vergroting.
Bereken de grootte van het beeld van de boom op de film.
PRACTICUM
Je krijgt bij dit proefwerk een enveloppe met lensje.
Bepaal zo goed mogelijk de brandpuntsafstand van jouw lensje en beschrijf hoe je dat
gedaan hebt. Het is niet de bedoeling dat je samenwerkt of gaat wandelen. Lever jouw
enveloppe met je lensje weer mee in. Mogelijk wil je graag weten dat de afstand tussen vloer
en TL-buizen 2.80 m is. Maar misschien schijnt de zon ook wel.
Als je de bomen in de verte als lichtbron gebruikt, komt het beeld op brandpuntsafstand: 17
cm.
Als je de TL-lampen gebruikt als lichtbron, je houdt de lens horizontaal en je ontwerpt een
scherp beeld op de tafel, dan moet je de tafelhoogte meten en aftrekken van de 2,80 m
plafondhoogte om de afstand voorwerp-beeld te bepalen. De beeldafstand kun je direct
meten. Je kent dan ook de voorwerpsafstand = lens-plafond en dan de lenzenformule
invullen.
BEELD
Je ziet hier een positieve lens
met het beeld, zoals dat
gevormd wordt van een ver
verwijderde lichtgevende pijl
met een lengte van 7,20 m..
Enige stralen van de punt van de
pijl zijn getekend.
De schaal van deze tekening is
1:1.
Bepaal hoever de lichtgevende
pijl van de lens verwijderd is.
UITWERKING:
Het voorwerp is 7,20 m; de pijl op het papier is 2,6 cm. Nameten!!
De vergroting is dus 1/277.
De beeldafstand is 5 cm Nameten!! het voorwerp stond dus 277×5 cm = 13,8 m van de lens.
a
LOEP
Een normaal ziende kunstkenner, n = 25 cm, bekijkt een sieraad van 1,0 cm lengte en brengt
het daarom op nabijheidsafstand van zijn oog.
Bereken onder welke hoek hij het voorwerp bekijkt.
b
Om details nader te bekijken gebruikt hij een loep, f = 3,0 cm, en plaatst het sieraad 2,0 cm
van de loep.
Construeer het beeld gevormd door de loep.
c
Onze kunstkenner houdt vervolgens het sieraad op 3,0 cm van de loep, zoals het hoort.
Construeer de lichtstraal die van de top A van het getekende sieraad door het optisch
midden van zijn oog gaat. Het sieraad, de loep en het oog zijn schematisch in de tekening
weergegeven.
UITWERKING:
A
B
C
=
s 1
0,040 rad = 2,29 ∘
r 25
.
De straal door het midden van de lens gaat rechtdoor. de bundel uit de lens is een
evenwijdige bundel, omdat het voorwerp in F staat. De straal uit die evenwijdige bundel die
midden door de ooglens gaat, gaat rechtdoor en is de gevraagde straal.
A
B
NORMAALZIENDE MET BRIL
Een normaal ziende (n = 25 cm) zet een bril op met een sterkte 1 dpt.
Ziet hij een voorwerp op 40 cm scherp?
Waar ligt zijn N met deze bril?
A
LERAAR
Je leraar natuurkunde is bijziende.
Hij heeft voor ver zien glazen nodig met S = 2,00 dpt.
Je leraar natuurkunde is inmiddels ook oudziende en heeft daardoor een
nabijheidspuntafstand van 25 cm. Terwijl hij dit tikt, bevinden zijn ogen zich 60 cm van het
beeldscherm.
Leid af of hij de letters op het beeldscherm zonder bril scherp kan zien.
B
Nadeel van negatieve lenzen is dat zij een verkleind beeld maken van een voorwerp.
Bereken de grootte van het door mijn bril gevormde beeld van een 24 cm groot voorwerp op
60 cm afstand van de bril.
C
Om goed te kunnen zien is een scherp beeld niet voldoende. Ook het ‘oplossend vermogen’
is van belang.
Kun je mij door een voorbeeld duidelijk maken wat ‘oplossend vermogen’ is?
a.
KAARSJE
Een verjaardagskaarsje KK' is nog maar 1,5 cm lang en staat op 4,0 cm voor een lens met
brandpuntsafstand f = 3,0 cm. Zie tekening. De lens zit in een ondoorzichtige lenshouder. De
diameter van de lens is 2,0 cm.
Construeer het beeld van het voorwerp KK'.
b.
c.
d.
Construeer het verloop van de bundel die vanuit top K door de lens gaat.
Bereken de grootte van het beeld als het kaarsje op 3,5 cm voor de lens wordt geplaatst. Ga
er gemakshalve maar vanuit dat de lengte van het kaarsje nog steeds 1,5 cm is.
Bereken de verhouding van de verlichtingssterkten van de beelden van het kaarsje, zoals die
ontstonden bij v = 4,0 cm en bij v = 3,5 cm.
a
b
c
d
UITWERKING:
We trekken de constructiestraal
door het midden en evenwijdig
aan de hoofdas. Die laatste
stippelen we omdat deze niet
door de lenshouder kan.
Alle stralen uit K via de lens
gaan naar het beeldpunt.
Lenzenformule levert b = 21 cm.
en vergrotingsformule geeft een
grootte van het beeld van 9,0 cm
Er zijn twee effecten.
Effect 1.
In de constructie is het beeld 4,5 cm lang.
In de berekening van onderdeel c is het 9,0 cm lang.
We hebben met een tweemaal zo lang beeld te maken. De oppervlakte is dus viermaal zo
groot.
Daardoor is de verlichtingssterkte viermaal zo klein.
Effect 2.
De kaars staat nu dichter bij de lens. Daardoor vangt de lens meer lichtop.
De afstandsverhouding is 4,0 : 3,5 De oppervlakteverhouding is 4,0² : 3,5² = 1,31.
Samen: Hij ontvangt ¼ * 1,31 = 0,33 zo weinig licht. De verlichtingssterkte is dus maar 0,33
keer de vorige waarde. Dat is 3,1 maal zo weinig.
DIA
Van een dia van 35 mm wil ik met een lens met f = 15 cm een beeld maken dat 1,00 m groot
is.
Bereken de afstand dia - beeld.
HET NORMALE OOG
Als je een voorwerp binnen de brandpuntsafstand van een positieve lens zet, ontstaat een
rechtopstaande vergroot beeld.
tekening 6
a.
De tekening hierboven is op schaal. De loep heeft een diameter, zoals getekend. Ook de
positie en de grootte van de pupil, het minder dik getekende deel van het oog, heeft de juiste
grootte. In dit vereenvoudigde model kun je ook net doen of de pupil samenvalt met de
ooglens.
Construeer het beeld dat door de loep van de pijl wordt gevormd in tekening 6.
tekening 7
b.
c.
Bij een juist gebruik van de loep plaatst men het voorwerp in het brandpunt, zoals in
tekening 7.
Teken in tekening 7 de bundel die vanuit de top van de pijl via de loep richting oog gaat.
Construeer in tekening 6 de lichtstraal die vanuit de top van de pijl via de loep door het
midden van de ooglens gaat.
d.
In tekening 6 bij vraag a, ontstaat van geen enkel punt van het voorwerp een scherp beeld
op het netvlies.
Leg uit waarom.
e
aanvullend:
Leid af van welk deel van de pijl een scherp beeld op het netvlies ontstaat.
f
In tekening 6 bij vraag a, ontstaat van geen enkel punt van het voorwerp een scherp beeld
op het netvlies.
Leg uit waarom.
UITWERKING
a.
b.
c.
a
LENS
Getekend zijn een voorwerp en het door een lens ervan gemaakt beeld. Het kleine pijltje stelt
het beeld voor. De schaal is 1:10.
Bepaal door constructie waar de lens zich de lens bevond en bepaal de plaats van
optisch midden en van de brandpunten.
Bereken met de te meten voorwerps- en beeldsafstand de brandpuntsafstand.
Geef in de tekening de plaats aan waar je de lens eveneens kunt zetten om op dezelfde
plaats een scherp beeld te vormen. Schrijf op hoe je die plaats gevonden hebt.
UITWERKING:
De stralen door het optisch midden gaan rechtdoor. Het snijpunt levert dus O.
De brandpunten vind je dan door te bedenken dat de stralen evenwijdig aan de hoofdas door
het brandpunt gaan.
1 1 1
1
1
1
f 30,6 cm
v b
f
106 43
f
b.
Je meet vanuit O resp. 10,6 cm en 4,3 cm en dus
c
In de lenzenformule komen v en b symmetrisch voor. Zet dus de lens even ver voor het
voorwerp als hij nu voor het beeld staat.
a.
b.
c.
a.
b.
c
OOG MET LENS
Ik ben bijziende, maar met mijn bril, f = - 50 cm, is dat probleem opgelost.
Met bril is mijn nabijheidspunt 40 cm.
Bereken de sterkte van mijn bril.
Bereken waar mijn nabijheidspunt zonder bril ligt. Met een goede tekening levert deze
opgave meer punten op.
Ik zit 10 m van de achterwand van de klas verwijderd.
Bereken de sterkte van de bril die ik nodig zou hebben om althans in de klas geen last van
mijn bijziendheid te hebben.
Uitwerking:
S=1/f = 1/(-0,50)=-2,0 dpt
Het nabijheidspunt speelt een rol
bij maximale accommodatie. Door
de negatieve bril komt dit verder
weg te liggen.
Zet je een voorwerp in N' dan
maakt de negatieve bril er een
beeld van in N.
1/v + 1/b = 1/f dus
1/40 + 1/b = 1/-50 dus b=-22 cm
Mijn vertepunt zonder bril ligt op 50 cm.
Met bril mag dat dus 10 m worden. Realiseer je dat v = 10 m en b = - 50 cm.
lenzenformule geeft 1/10 + 1/(-50)=1.f=S dus S=-1,9 dpt
LENS
Een lens levert een 600 maal vergroot beeld op een 50 m van het voorwerp verwijderd
scherm.
Bereken de brandpuntsafstand.
a
b
c
LENS EN SPIEGEL
Op
brandpuntsafstand, ƒ
= 4,0 cm, voor een
positieve lens staat
een pijlvormig
voorwerp. Aan de
andere kant van de
lens bevindt zich,
eveneens op
brandpuntsafstand,
een vlakke spiegel.
Construeer het beeld
van de pijl, gevormd
door de combinatie
van lens en spiegel.
Construeer het
verdere verloop van
de getekende straal
uit de top van de pijl.
Bereken de plaats van het beeld als het voorwerp zich op 20,0 cm voor de lens bevindt.
UITWERKING:
In de meeste gevallen is het het
gemakkelijkst om uit te gaan van een punt
dat niet op de hoofdas ligt. In dit geval ben
je het snelst klaar door dat juist wel te
doen. Zie de vette 'open' streeplijn. Die
gaat van brandpunt naar lens, dan
evenwijdig aan hoofdas, komt net zo terug
en eindigt dus in het brandpunt. De voet
van de pijl wordt op zichzelf afgebeeld.
Straal 1 levert ook geen problemen.
Evenwijdig aan hoofdas, dus naar
hoofdbrandpunt (2), kaatst terug (3) en
gaat als straal uit F evenwijdig verder:4.
Dus beeld van de punt moet op die
'hoogte' liggen. Beeld is omgekeerde pijl.
c.
Ga je op de 'gewone' manier te werk, dan teken je eerst straal 1-2-3-4.
Om het beeldpunt te vinden heb je een tweede straal nodig. Daarvoor kies je a. a is
evenwijdig aan bij-as b en breekt dus naar bijbrandpunt F'. Kaatst dan terug: d.
d is evenwijdig aan bij-as e en breekt dus naar bijbrandpunt F''. Daarmee is het snijpunt en
dus ook het beeld gevonden. Tevens is vraag b. beantwoord.
lenzenformule: v1=20 cm en f=4 cm b1 = 5 cm
na spiegeling: v2 = 8 cm en f= 4 cm b2 = - 12 cm
Door de spiegel wordt het beeld dat 5 cm achter de lens terecht kwam, een beeld op maar 3
cm erachter. Het is dit beeld dat als voorwerp voor de 'terugweg' fungeert.
Het uiteindelijke beeld is een virtueel beeld 12 cm achter de lens.
HURT
Hieronder zie je een tekening. Deze is gemaakt naar een foto. We hebben dat gedaan omdat
de opgave anders teveel geheugenruimte van de computer in beslag neemt. Het is de foto
van een bekend politicus, Douglas Hurd, gedeeltelijk gezien door zijn eigen bril.
a.
b.
c.
Is Douglas Hurd bijziend of verziend?
Welk oog heeft de sterkste afwijking van een normaal oog?
De foto werd gemaakt met een telelens, f = 200 mm. En het negatief, 24 mm × 36 mm, werd
in zijn doka vergroot tot een foto van 16 bij 24 cm. In het vergrotingsapparaat zat een bolle
lens met een brandpunmtsafstand van 5,0 cm.
Bereken de afstand tussen het negatief en het fotografisch papier tijdens het vergroten in de
doka.
d.
De breedte van de bril is op de foto 76 mm, maar in werkelijkheid 136 mm.
Bereken hoever de fotograaf van de politicus stond tijdens het maken van de foto.
e.
f.
Door het rechter brilleglas, links op de foto, zie je beide ogen en de neus van de minister
sterk verkleind. Iemans zonder natuurkunde in zijn pakket snapt niet hoe dat kan. Jullie
weten dat we het verkleinde virtuele beeld van zijn gezicht waarnemen. Douglas houdt de
bril 20 cm vóór zijn gezicht vast.
Bepaal door opmeten in de foto de vergroting bij deze waarneming.
Bereken hieruit de sterkte van zijn rechter brilleglas.
a.
b.
c.
d.
Uitwerking:
bijziend
rechteroog
foto 24 cm breed, maar negatief 36 mm, dus een vergroting 6,67 ×.
De afstand van negatief tot fotopapier is b + v = 44 cm.
b
N 6,67 b 6,67 v
v
1 1
1
1
1
1
v 5,8 cm en b 38,3 cm
v b
f
v 6,67 v 5,0
76 mm
11,4 mm
De breedte van de bril op het negatief is
6,67
N
b 11,4
b
0,0838
v 136
v
1 1
1
1
1
1
v b
f
v 0,0838 v 20,0
e.
Hieruit volgt v = 259 cm. Je kunt hier nog 22 cm voor b bijtellen.
De afstand tot de bril moet dus 2,8 m zijn geweest.
We meten de pupilafstand 'gewoon' en door het brilleglas: resp 23 en 8 mm.
f
N
b
8
0,35
v
23
b
8
b
N
b 6,96 cm
v
23 20
1
1 1
1
1
9,4 m -1
f
v b
0,20 0,0696
Dit betekent dus een sterkte S = - 9,4 dpt en een f = - 10,7 cm.
LENZENPAAR
Twee lenzen, beide met een f = 3,0 cm, staan op 3,0 cm van elkaar. Op 2,0 cm voor de
eerste lens staat een 1,0 cm groot voorwerp.
a.
b.
c.
d.
Bereken de beeldafstand van het door de combinatie van beide lenzen gemaakte beeld.
Bedenk hierbij dat het door de eerste lens gevormde beeld het voorwerp voor de tweede
lens is.
Construeer het beeld gevormd door de lenzencombinatie.
De persoon waarvan alleen het oog geschetst is, is bijziende en heeft een nabijheidsafstand
van 12 cm. Beredeneer of deze de pijl scherp kan zien in de getekende situatie.
Geef globaal de positie van het stuk netvlies aan, waarop de pijl wordt afgebeeld.
PUPIL
Voor onderzoek krijgt een patiënt pupilverwijdende druppel toegediend. Deze druppels
hebben geen invloed op de werking van het accommodatievermogen van het oog.
Leg uit waarom het de patiënt verboden is om zelf achter het stuur van zijn auto te kruipen te
naar huis te rijden.
VOOR DE SPIEGEL
Als bijziende met een vertepunt op 1,00 m en nabijheidspunt op 0,15 m sta ik voor de spiegel
en kijk mezelf in de ogen.
Leid af op welke afstand ik van de spiegel moet staan om mijn ogen scherp te kunnen zien.
Uitwerking:
Zaken die zich bevinden tussen 0,15 m en 1,00 m kan ik scherp zien. De spiegelbeelden waar
ik naar kijk moeten zich dus tussen die twee afstanden bevinden.
Het spiegelbeeld staat even ver achter de spiegel als het origineel ervoor. De afstand spiegel
origineel is dus de helft van de afstand origineel-spiegelbeeld.
Het origineel moet dus tussen de 0,15:2 = 0,075 m en 1,00:2 = 0,50 m van de spiegel zitten.
LENS
De getekende lens heeft een brandpuntsafstand van 5,0 cm. Vóór deze lens staat als voorwerp
een lamp L. De voorwerpsafstand is 3,0 cm. De diameter van de lens is 2,0 cm. Het licht van
de lamp komt uiteindelijk op het scherm terecht. De afstand van het scherm tot de lens is
8,0 cm
Construeer en arceer de bundel die vanuit de lamp door de lens gaat en op het scherm terecht
komt.
TOREN
Ten behoeve van een folder moet een gebouw van 40 cm hoogte in een maquette worden
gefotografeerd. De lens van de camera staat 2,00 m van het gebouw vandaan. De lens heeft
een diafragma-opening met een diameter van 4 mm
Op het negatief is het gebouw 30 mm hoog.
Bereken de brandpuntsafstand van de gebruikte lens.
De camera wordt vervangen door een camera op dezelfde plaats met een lens van dezelfde
sterkte, maar er wordt gebruik gemaakt van een diafragma van 20 mm.
Leid af in welke opzichten het beeld anders zal zijn. Denk hierbij aan beeldgrootte, scherpte,
scherptediepte en verlichtingssterkte.
Uitwerking:
N
b
3
3
b
200 15 cm
v 40
40
1 1 1
1
1
1
f 13,9 cm
v b
f
200 15
f
v en f onveranderd, dus ook b en N. Aan de grootte van het beeld en de scherpte is dus niets
veranderd. De scherptediepte hangt af van de grootte van de vlekjes die op het negatief
ontstaan, omdat niet alle afgebeelde voorwerpen op de goede voorwerpsafstand staan. De
grootte van deze vlekjes hangt direct af van de gebruikte lensdiameter. Als die 4× zo groot
wordt, dan ook die vlekjes. De scherptediepte neemt dus af.
Als de diafragma-opening 4× zo groot wordt en de gebruikte lensoppervlakte dus 4²× zo
groot, komt er 16× zo veel licht op het negatief. De verlichtingssterkte ervan is dus 16× zo
groot.
LENS – CONSTRUCTIE 2
Getekend is een lens met brandpunt en een voorwerp ervoor.
Construeer het beeld dat de lens van het voorwerp vormt.
We construeren het beeld van de ‘bovenkant’ en kennen dan ook de positie van de
‘onderkant’ Het beeld is virtueel en moet dus gestippeld worden volgens de afspraak
LENS – CONSTRUCTIE 1
Getekend is een lens met zijn brandpunt. In de richting van de lens gaat een lichtstraal.
Construeer het verdere verloop van de lichtstraal
Uitwerking:
optie 1: De groene stralen. We beschouwen het begin van de getekende straal als een lamp.
Daarvan hebben we via constructiestralen het beeld proberen te construeren; helaas net over
de rand. Ook de gegeven straal moet daar doorheen.
optie 2: Kies op de getekende straal het punt L op afstand ƒ van de lens.
Van lampen in het brandpunt treedt een evenwijdige bundel uit de lens. Dus teken je de rode
straal door het midden, dan weet je ook de richting van de andere stralen die uit de lens
komen.
LENS – BEREKENING
De camera waarmee ik foto’s maak, heeft een lens met een brandpuntsafstand van 50 mm.
Het voorwerp dat ik fotografeer, komt met een vergroting N = 0,050 op het negatief.
Bereken de afstand voorwerp – negatief.
Uitwerking:
1 1 1
1 1
1
v b
f
v b 50
en N
b
b
0,050 b 0,050v
v
v
1
1
1
vul dit laatste in in de lenzenformule: v 0,050v 50 v 1050 en b = 52,5.
Alles in millimeters. De gevraagde afstand is b + v = 1102,5 mm = 1,1 m.
LENS – GRAFISCH
Bij een bepaalde lens hoort onderstaande b,v-grafiek.
a
b
Bepaal de brandpuntafstand van deze lens.
Bepaal met behulp van deze grafiek bij welke beeldafstand een vergroting N = 3 hoort. Teken
daartoe eerst in de grafiek de lijn die hoort bij N = 3
Uitwerking:
a
1 1 1
1
1
1
f 11 cm
v b f
20 26 f
b
Voor een grotere nauwkeurigheid kun je van meer punten
berekenen wat ƒ oplevert en dat middelen.
N = 3 betekent b = 3v en dus een rechte door de oorsprong met
hellingsgetal 3.
Het snijpunt bij b = 44 cm is de gevraagde beeldafstand.











