wetten van Newton

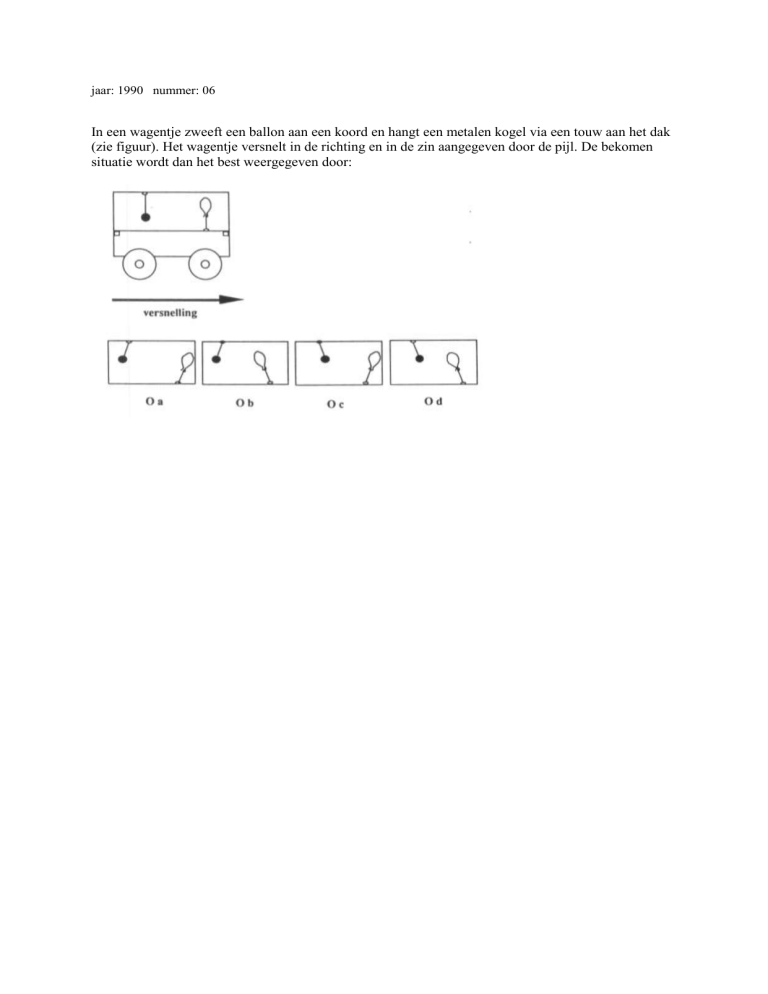
jaar: 1990 nummer: 06
In een wagentje zweeft een ballon aan een koord en hangt een metalen kogel via een touw aan het dak
(zie figuur). Het wagentje versnelt in de richting en in de zin aangegeven door de pijl. De bekomen
situatie wordt dan het best weergegeven door:
jaar: 1991 nummer: 05
Twee blokken met respectievelijke massa's m1 en m2rusten op een horizontaal vlak. De wrijving tussen
de blokken en het horizontale vlak mag verwaarloosd worden. Op het blok met massa ml werkt een

horizontale kracht
F waardoor beide blokken in beweging komen.
De kracht die blok 1 op blok 2 uitoefent is dan
0a.
m1 
F
m2
m1 
F
m1  m 2

m2
0c.
F
m1  m 2

0 b. F
0 b.
jaar: 1992 nummer: 11
Op een massa van 5 kg werkt in de x-richting een kracht Fx die in het onderstaande diagram als
functie van de positie wordt voorgesteld.
Indien de massa vanuit rust vertrekt in x= 0 m , bedraagt zijn snelheid in het punt x=6 m
O a.
O b.
O c.
0 d.
3 m/s.
6 m/s.
9 m/s.
12 m/s.
jaar: 1994 nummer: 05
Op de onderstaande figuren zijn telkens de krachten aangegeven die op de banden van de fiets
inwerken. De krachten grijpen aan op de plaats waar de banden contact maken met de grond.
De fiets versnelt in de richting en de zin aangegeven door de vector a .
De figuur die een juiste weergave geeft van de krachtwerking op de banden is dan
jaar: 1996 nummer: 06
£eu wagentje kan wrijvingsloos voortbewegen over een horizontale tafel. Het wagentje zit vast aan een
touw. Het touw loopt via oen katrol op de rand van de tafel wrijvingsloos naar een plaatje P. Bij
aanvang liggen op het wagentje zeven gelijke massa's.
Men voert nu zeven metingen uit waarbij men telkens een massa m van het wagentje neemt en
toevoegt aan het plaatje P. De totale massa op het wagentje vermindert dus bij iedere meting terwijl
die van het plaatje P met eenzelfde bedrag toeneemt. Telkens laat men het wagentje starten vanuit
eenzelfde positie en bepaalt de snelheid v die het plaatje P heeft op het ogenblik dat het op de grond
botst.
De massa van het lege wagentje is 2m. De massa van het plaatje P is verwaarloosbaar.
Welke van de onderstaande grafieken geeft dan het best de snelheid v weer als functie van het aantal
massa's op het plaatje P 1 De schaal van de v-as is lineair.
jaar: 1998 nummer: 04
Twee massa's van respectievelijk 4 kg en 12 kg zijn met elkaar verbonden via een touw. Het touw
hangt over een ronde balk waarover het wrijvingsloos kan glijden.
De massa van 12 kg bevindt zich aanvankelijk op 2 meter van een horizontale vloer. Deze situatie is
weergegeven in de onderstaande figuur.
De figuur stelt de beginsituatie voor.
Als de massa's vanuit rust worden losgelaten, dan bereikt de massa van 12 kg de vloer met een
snelheid van
O a.
20 m/s.
O b.
40 m/s.
O c.
20 m/s.
O d.
80 m/s.
jaar: 1998 nummer: 05
Een persoon van 80 kg hangt aan een luchtballon. De kracht in het opnangtouw wordt afgelezen op
een dynamometer D.
Als de persoon, gedurende een bepaald tijdsinterval, op de dynamometer 760 N afleest, dan kan men
zeggen dat de ballon gedurende dat tijdsinterval:
O a.
O b.
O c.
O d.
stijgt met een constante snelheid.
daalt met een constante versnelling
stijgt met een constante versnelling.
daalt met een constante snelheid .
jaar: 1998 nummer: 06
Een op de achterwielen aangedreven auto rijdt met een toenemende snelheid achteruit.
De horizontale componenten van de krachten die de voorste en de achterste banden op het wegdek
uitoefenen kunnen dan best aangegeven worden door figuur:
jaar: 1999 nummer: 27
Een liftcabine zoals getekend in onderstaande figuur wordt opgehaald in de liftkoker aan een
staalkabel. Verwaarloos alle wrijving.
Wanneer de liftcabine naar omhoog beweegt met constante snelheid, kunnen we zeggen dat:
O a.
de grootte van de spankracht in de kabel groter is dan de grootte van de zwaartekracht.
O b. de grootte van de spankracht in de kabel gelijk is aan de grootte van de zwaartekracht.
O c.
de grootte van de spankracht in de kabel kleiner is dan de grootte van de zwaartekracht.
O d. de cabine naar omhoog gaat omdat de kabel ingekort wordt, en niet omwille van de kracht die
de kabel uitoefent op de liftcabine.
jaar: 1999 nummer: 30
Vier massa's, oorspronkelijk in rust, zijn met massaloze touwen verbonden zoals voorgesteld op de
figuur. De massa van ieder van de massa's is eveneens aangegeven op de figuur.
Het touw tussen massa 4 en 3 loopt over een staaf S. Verwaarloos alle wrijving.
De kracht in het touw tussen massa 1 en massa 2 is dan gelijk aan:
O a.
O b.
O c.
O d.
0,2 mg.
0,8 mg.
1,0 mg.
4,0 mg.
jaar: 2000 nummer: 23
De vier massa's uit de situatie voorgesteld door de figuur zijn identiek. Ze zijn verbonden door
massaloze touwen. De ideale katrol (K) vertoont geen wrijving. De blokken bewegen wrijvingsloos
over de tafel en elke andere vorm van wrijving wordt eveneens verwaarloosd.
De grootte van de spankracht in het touw op plaats 1 noemen we F1. De grootte van de spankracht in
het touw op plaats 3 noemen we F3.
Er geldt dan:
O a.
O b.
O c.
O d.
F1/F3 = 1/3 .
F1/F3 = 1 .
F1/F3 = 2 .
F1/F3 = 3 .
jaar: 2001 nummer: 24
Twee stalen knikkers 1 en 2 worden gelijktijdig losgelaten uit een punt O op twee vlakken met
verschillende helling (zie figuur). We bekijken de knikkers aan de voet van de hellingen.
Dan geldt:
O a. beide knikkers komen met even grote snelheid en op hetzelfde tijdstip aan.
O b. de versnelling van 1 is groter dan van 2, maar 1 komt met een grotere snelheid eerst aan.
O c. de massa's van 1 en 2 moeten gekend zijn om hun versnelling te kunnen berekenen en uitspraken
te kunnen doen over hun snelheid.
O d. knikker 1 komt eerder aan. De versnelling van 1 is groter dan deze van 2 maar zijn snelheid is
even groot als deze van knikker 2.
jaar: 2001 nummer: 26
Twee voorwerpen (m = 10,0 kg en M = 15,0 kg) zijn verbonden met een niet uitrekbaar massaloos
touw (zie figuur) dat breekt als de spankracht groter is dan 145N.
Het systeem vertrekt vanuit stilstand. De versnelling is 2,00 m/s2 zolang het touw niet breekt.
De spankracht in het touw is dan gelijk aan:
O a. 100 N.
O b. 120 N.
O c. 140 N.
O d. de vraag heeft geen zin want het touw breekt.