Samenvatting: boek "Linear Algebra and Its Applications

lOMoARcPSD
Samenvatting Lineaire Algebra, periode 4
Hoofdstuk 5, Eigenwaarden en eigenvectoren
5.1; Eigenvectoren en eigenwaarden
Definitie:
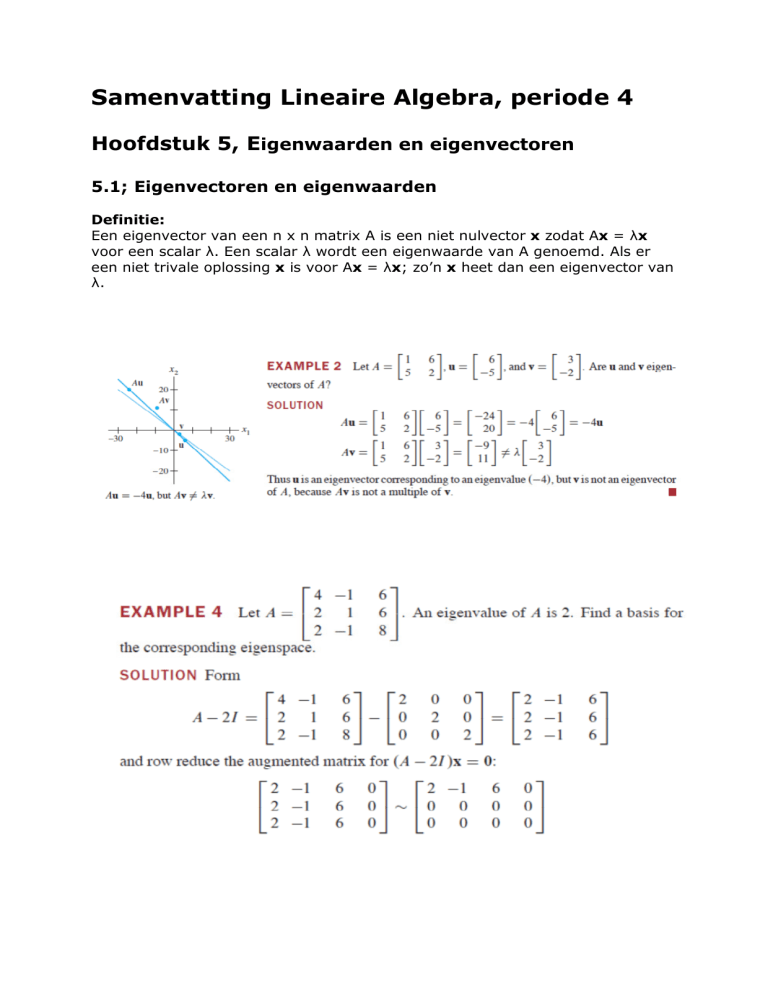
Een eigenvector van een n x n matrix A is een niet nulvector x zodat Ax = λx
voor een scalar λ. Een scalar λ wordt een eigenwaarde van A genoemd. Als er
een niet trivale oplossing x is voor Ax = λx; zo’n x heet dan een eigenvector van
λ.
lOMoARcPSD
Theorema 5.1
De eigenwaarden van een driehoeks matrix zijn gelijk aan de waarden op de
diagonaal.
Theorema 5.2
Als v1, … , vr eigenvectors zijn die corresponderen met een zelfde aantal
eigenwaarden λ1, …, λr van een n x n matrix A, dan is de set { v1, … , vr} lineair
onafhankelijk.
lOMoARcPSD
5.2 Karakteristieke vergelijking
Inverteerbare matrix theorie
a. A is een inverteerbare Matrix
b. A is rij equivalent met de n x n identiteitsmatrix
c. A heeft n pivot posities
d. De vergelijking Ax = 0 heeft alleen de triviale oplossing
e. De kolommen van A zijn lineair onafhankelijk
f. De lineaire transformatie x Ax is 1-op-1
g. De vergelijking Ax = b heeft op zijn minst 1 oplossing voor elke b in ℝn
h. De kolommen van A spannen ℝn
i. De lineaire vergelijking x Ax beeld ℝn af in ℝn
j. Er is een n x n matrix C zodat CA = I
k. Er is een n x n matrix D zodat AD = I
l. AT is een inverteerbare matrix
m. De kolommen van A vormen een basis voor ℝn
n. Col A = ℝn
o. dim Col A = n
p. rank A = n
q. Nul A = {0}
r. dim Nul A = 0
s. het getal 0 is geen eigenwaarde van A
t. de determinant van A is niet 0
lOMoARcPSD
Theorema 5.3
Eigenschappen van determinanten
A en B zijn n x n matrices
a.
b.
c.
d.
A is alleen inverteerbaar als det A ≠ 0
Det AB = (det A)*(det B)
Det AT = det A
Als A driehoekig is, dan is det A het product van de waarden op de
diagonaal van A
e. Een rij reductie op matrix A veranderd de determinant niet. Het
verwisselen van een rij veranderd het teken. En schaling van een rij zorgt
voor de zelfde schaling van de determinant
Karakteristieke vergelijking
Een scalar λ is alleen een eigenwaarde van een n x n matrix A als λ voldoet aan
de volgende karakteristieke vergelijking
− = Theorema 5.4
Als n x n matrixen A en B soortgelijk zijn, dan hebben ze dezelfde karakteristieke
polynoom en daarom de zelfde eigenwaarden, met dezelfde multipliciteiten.
lOMoARcPSD
5.3 Diagonalisatie
Theorema 5.5 De diagonalisatie theorie
Een n x n matrix A is alleen diagonalizeerbaar als A n lineair onafhankelijke
eigenvectoren heeft.
In feite, A = PDP-1 met D een diagonale matrix, alleen als de kolommen van P n
lineair onafhankelijke eigenvectoren zijn van A. zodat de diagonale waarden van
D de corresponderende eigenwaarden zijn van A
Stappenplan voor diagonalizeren
A is een 3 x 3 matrix
Stap 1 vindt de eigenwaarden van A, d.m.v. de karakteristieke vergelijking
Stap 2 vindt de drie lineair onafhankelijke eigenvectoren van A
Stap 3 vorm P met de vectoren van stap 2
Stap 4 vorm D met de corresponderende eigenwaarden
lOMoARcPSD
Theorema 5.6
Als een n x n matrix met n verschillende eigenwaarden dan is de matrix
diagonalizeerbaar. (dit is geen vereiste)
Theorema 5.7
A is een n x n matrix met verschillende eigenwaarden λ1, …, λp
a. Voor 1 ≤ k ≤ p, de dimensie van de eigenruimte van λk is minder dan of
gelijk aan de multipliciteit van λk
b. De matrix A is diagonalizeerbaar als de som van de dimensies van de
verschillende eigenruimtes gelijk is aan n. dit kan alleen als de
dimensie van de eigenruimte van λk voor elke λk gelijk is aan de
multipliciteit van λk
c. Als A diagonalizeerbaar is en βk is een basis voor de eigenruimte
corresponderend met λk voor elke k, dan vormt de totale collectie van
vectoren β1, …, βp een eigenvector basis voor ℝn
5.4 Eigenvectoren en lineaire transformaties
lOMoARcPSD
lOMoARcPSD
Theorema 5.8 Diagonale matrix representatie
Stel dat A = PDP-1 waarbij D een diagonale n x n matrix is. Als B een basis is
voor ℝn gevormd vanuit de kollommen van P, dan is D de B-matrix voor de
transformatie xAx
lOMoARcPSD
5.5 Complexe Eigenwaarden
lOMoARcPSD
lOMoARcPSD
-
r>1 groter wordende spiraal met de klok mee
r=1 cirkel/ellips met de klok mee
0<r<1 kleiner wordende spiraal met de klok mee
5.6 Discrete Dynamische Systemen
lOMoARcPSD
lOMoARcPSD
Als alle groter zijn dan 1, dan heb je een repellor
Als alle kleiner zijn dan 1, dan heb je een attractor
En als éé > |1|éé < |1| dan heb je een zadelpunt
lOMoARcPSD
Hoofdstuk 6, Orthogonaliteit en kleinste kwadraten
6.1 In product
Theorema 6.1
u, v, en w zijn vectors in ℝn en c is een scalar
a. u ● v = v ● u
b. (u + v) ● w = u ● w + v ● w
c. (cu) ● v = c(u ● v) = u ● (cv)
d. u ● u ≥ 0 and u ● u = 0 alleen als u = 0
e. ||cv|| = |c|*||v|| = ●
= ∗ ●
= ∗ √●
Definition
De lengte van een vector v is gedefinieerd door
||v|| = √● = + ⋯ + !
|||| = ●
Definition
De afstand tussen twee vectoren , geschreven als dist(u,v) is de lengte van de
vector u – v.
"#$%&, = ||& − ||
Definition
Twee vectoren zijn orthogonaal als het inproduct van de vectoren 0 is
(● = Theorema 6.2 Pythagoras regel
Twee vectors u en v zijn orthogonaal als ||& + || = ||&|| + ||||
Een vector x is in ) * alleen als x orthogonaal is met elke vector uit een set die
W spant, ) * is een subspace van ℝn. Zie ook de afbeelding: L = ) * .
Theorema 6.3
Als A een m x n matrix is, en het orthogonale complement van de rij ruimte van
A is de nul ruimte van A , en het orthogonale complement van de kolomruimte
van A is de nul ruimte getransponeerd.
+,-.
= /01.2"3,1.
* = /01.*
lOMoARcPSD
6.2 Orthogonale sets
Theorema 6.4
een verzameling van vectoren {v1,…,vk} is een orthogonale verzameling als elk
tweetal vectoren loodrecht op elkaar staat, en er geen nul-vector in zit.
Definitie
een orthogonale basis voor een deelruimte W van ℝn is een basis voor W en is
ook een orthogonale verzameling.
Theorema 6.5
Een set {u1,…,up} is een orthogonale basis voor een deelruimte W van ℝn. voor
elke y in W zijn de gewichten in de lineaire combinatie
4 = & + ⋯ + 5 &5
Zijn gegeven door
4●&6 6 = 7 = 1, … , 9
&6 ●&6
lOMoARcPSD
Definitie
Een orthonormale verzameling is een orthogonale verzameling waarin de
vectoren allemaal lengte 1 hebben.
Theorema 6.6
Een m x n matrix U heeft orthonormale kolommen als : ; : = <
Theorema 6.7
U is een m x n matrix met orthonormale kolommen en x en y zijn in ℝn dan:
a. =|:>|= = ||x||
b. :>
●:4
= >●4
c. Als U een vierkante matrix is met orthonormale kolommen dan is U
inverteerbaar en is U-1 = UT. zon matrix heet een orthogonale matrix
6.3 Orthogonale projecties
Theorema 6.8
Als W is een deelruimte is van ℝn. dan kan elke dan kan elke y in ℝn geschreven
worden in de vorm
?+@
4=4
? is in W en z is in ) * . In feite als {u1, … , up} een orthogonale basis is
Waar 4
voor W dan:
? = 9A,7B 4 =
4
?
En @ = 4 − 4
4●&D
4●&C
&C + ⋯ + &
&C ●&C
&D ●&D D
Er zijn 3 interpretaties:
? + @ met 4
? in W en @ ⊥ )
1. y ontbinden in 4
? is een orthogonale projectie van y op W
2. 4
3. De afstand van y tot W is ||z||
lOMoARcPSD
Theorema 6.9
? is de
Als W een deelruimte is van ℝn, en y is een willekeurige vector in ℝn en 4
? het dichtstbijzijnde punt in W vanaf
orthogonale projectie van y op W, Dan is 4
y. dat houd in dat:
?|| < ||4 − ||
||4 − 4
?
Voor elke v in W niet gelijk aan 4
Theorema 6.10
Als de span{u1, … , up} een orthonormale basis is voor deelruimte W in ℝn dan:
9A,7F 4 = 4●& & + ⋯ + G4●&5 H&5
Als U = [u1 u2 … up] dan:
9A,7F 4 = :: ; 4, ,,A2114#ℝ!
lOMoARcPSD
6.4 Gram Schmidt
Theorema 6.11
lOMoARcPSD
Theorema 6.12
lOMoARcPSD
6.5 Kleinste Kwadraten methode
lOMoARcPSD
6.6 Toepassingen
lOMoARcPSD
Hoofdstuk 7,
Symmetrische matrices en kwadratische vormen
7.1 Diagonalisatie van symmetrische matrices
Theorema 7.1
Als A een symmetrische matrix is, dan geldt voor elke verschillende eigenwaarde
van A dat de bijbehorende eigenvectoren loodrecht op elkaar staan
Theorema 7.2
Een n x n matrix A is orthogonaal diagonaliseerbaar alleen als A een
symmetrische matrix is
lOMoARcPSD
lOMoARcPSD
Theorema 7.3
7.2 Kwadratische vormen
lOMoARcPSD
lOMoARcPSD
Theorema 7.4
lOMoARcPSD
Theorema 7.5