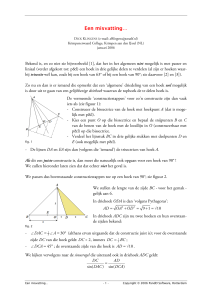
Inleiding - Wikiwijs Maken

Inleiding
Deze basisconstructies worden aan de leerlingen gegeven in de vorm van werkbladen
voor zelfstandig werken.
Met behulp van een beginschets van de gegevens en de constructiebeschrijving maken
de leerlingen de constructie zelfstandig.
Deze manier van werken dient mede om het zelfstandig werken te bevorderen en om te
leren om geschreven opdarchten uit te voeren. Nauwkeurig lezen wordt daarmee ook
geoefend.
Later in de periode zullen de verschillende constructies ook op meetkundige juistheid
bewezen worden. Daarbij worden meestal congruente dierhoeken gebruikt.
Daarvoor echter moeten de vijf congruentiegevallen behandeld zijn en die rusten op de
vijf constructie gevallen van driehoeken.
1
Het midden van een lijnstuk
Basisconstructie 1:
Een lijnstuk door midden delen.
Gegeven: Het lijnstuk AB
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
Neem vanuit A een afstand tussen de benen van de passer die wat groter is dan
van A tot het geschatte midden van AB
Cirkel vanuit A die afstand om aan beide kanten van AB (dus zowel boven AB,
als ook onder AB)
Doe het zelfde vanuit B (ook weer boven en onder het lijnstuk)
Zo ontstaan twee boogjes. We noemen de snijpunten C (boven) en D (onder)
Verbind de punten C en D met elkaar
Waar deze lijn AB snijdt, ligt het midden van AB, dan noem je M
M is het gevraagde midden van lijnstuk AB
Opmerking:
Met deze constructie heb je tegelijkertijd ook de middelloodlijn van het lijnstuk AB
geconstrueerd. CD is de lijn die loodrecht staat op AB en door het midden van AB
gaat. Dat is de middelloodlijn van AB.
2
Verplaatsen van een hoek
Basisconstructie 2
Een hoek te construeren, die gelijk is aan een gegeven hoek. (Verplaatsen van een hoek
naar een andere plaats op het papier)
Gegeven:
Hoek A
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
Trek een lijn m, waarop ∠A moet worden overgebracht en geef aan waar punt
A 0 komt. (A 0 is het nieuwe punt A en dat wordt weergegeven door een A met
een komma. Dat noemen we “accent”. Dus: ∠A-accent)
Trek in de gegeven hoek vanuit A een cirkel met willekeurige straal, dat geeft je
de punten B en C.
Trek vanuit A 0 een cirkelboog met dezelfde straal dat geeft je punt B 0 op lijn m
Neem de afstand BC van de gegeven hoek in de passer. Breng deze afstand over
naar de nieuwe driehoek en zet passer in B 0 en cirkel om op de cirkelboog om
A 0 dat geeft punt C 0
De hoek B 0 A 0 C 0 is de verplaatste hoek.
Opmerking: Je kunt de hoek zien als een soort krokodillenbek die open staat. Hoe ver
staat de krokodillenbek open? Dat wordt precies weergegeven door de afstand BC!
Deze constructie komt vaak voor.
3
Evenwijdige lijn
Basisconstructie 3
Door een punt buiten een gegeven lijn een andere lijn construeren, die evenwijdig is
aan de gegeven lijn.
Gegeven:
Een lijn l en een punt “ergens” buiten die lijn
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
Trek door P een willekeurige lijn m. Snijpunt van l en m is A
We gaan nu ∠CAB verplaatsen naar punt P volgens basisconstructie nr. 1 (verplaatsen van een hoek)
Trek een cirkelboog met willekeurige straal en A als middelpunt. Dit levert snijpunten B (op lijn l) en C (op lijn m)
Neem de afstand AB als straal in de passer en cirkel dit om vanuit P. Het
snijpunt van deze cirkel met lijn m noemen we D
Neem de afstand BC tussen de benen van de passer. Dit is hoe ver de “krokodillenbek” van ∠A open staat. Breng over naar D en cirkel af vanuit D hoe ver
de krokodillenbek open staat. Dit levert punt E
Trek een lijn door de punten E en P. Dit is lijn n. Lijn n is evenwijdig aan lijn
l. (symbool voor evenwijdig: k; dus: n k l )
We hebben nu ∠CAB verplaatst naar punt P. ∠DPEis evengroot als ∠CAB. De lijn
n door E en P is de gevraagde lijn.
4
Bissectrice
Basisconstructie 4
Een hoek door midden delen.
Een lijn die een hoek door midden deelt heet een bissectrice of deellijn.
Gegeven:
Hoek A
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
Zet de passer in A en trek een cirkelboog met willekeurige straal, die de benen
van∠A snijdt
Noem de beide snijpunten B en C
Teken nu twee cirkelboogjes met dezelfde straal, één vanuit B en één vanuit C
dat geeft het punt P
Trek de lijn AP De lijn AP is de gevraagde bissectrice.
5
Bissectricepaar
Basisconstructie 5
De bissectrices van twee nevenhoeken
Twee snijdende lijnen vormen vier hoeken, twee aan twee nevenhoeken.
Gegeven: een hoek A en zijn nevenhoek.
Construeer de bissectrices van deze hoeken en kijk wat je
opvalt.
Constructie beschrijving:
Construeer volgens basisconstructie 4 de bissectrices van hoek A en ook van zijn
nevenhoek.
Merk op, dat de beide bissectrices loodrecht op elkaar staan, ofwel een hoek van 90◦
vormen.
Eigenschap: De bissectrices van twee nevenhoeken staan loodrecht op elkaar
Te bewijzen ∠A23 = 90◦
Bewijs:
De hoeken ∠A1 , ∠A2 , ∠A3 en ∠A4 vormen een gestrekte
hoek.
Dus: ∠A1 + ∠A2 + ∠A3 + ∠A4 = 180◦
(1)
Omdat AP en AQ bissectrices zijn, geldt: ∠A1 = ∠A2 en
∠A3 = ∠A4
Vervang in (1) ∠A1 door ∠A2 en ∠A4 door ∠A3
Dan krijg je ∠A2 + ∠A2 + ∠A3 + ∠A3 = 180◦
Ofwel: 2 · ∠A2 + 2 · ∠A3 = 180◦
Delen door 2 geeft: ∠A2 + ∠A3 = ∠A23 = 90◦
6
Loodlijn oprichten
Basisconstructie 6:
In een punt van een lijn, een loodlijn op die lijn op te richten.
Gegeven: lijn l en een punt P op l.
In feite komt deze constructie neer op het construeren van
de bissctrice van een gestrekte hoek.
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
ˆ
Neem de passer met willekeurige straal en pas aan beide kanten van P gelijke
stukken af op lijn l. Zo ontstaan de punten A en B. Daarvoor geldt: PA = PB
Neem tussen de benen van de passer een afstand die een paar cm groter is dan
PA en cirkel dit af vanuit A, boven de lijn l
Cirkel dezelfde boog ook om vanuit B (ook boven lijn l)
Waar de bogen elkaar kruisen ontstaat punt C
Trek PC
PC is de gevraagde loodlijn.
7
Loodlijn neerlaten
Basisconstructie 7:
Hoogtelijn uit punt P neerlaten.
Gegeven: een lijn l en een punt P buiten lijn l.
Constructie beschrijving:
ˆ
ˆ
ˆ
Trek vanuit P een cirkelboog die lijn l twee maal snijdt. Noem de snijpunten A
en B.
Bepaal met basisconstructie 1 het midden van lijnstuk AB. Dit noem je M.
Trek lijn PM. Deze lijn is de gevraagde hoogtelijn.
8
Een hoek van 60◦
Basisconstructie 8 Constructie van een hoek van 60◦ (op een lijnstuk)
Gegeven:
Een willekeurig lijnstuk AB.
Constructie beschrijving:
ˆ
ˆ
ˆ
Trek een willekeurig lijnstuk AB (neem voor het gemak ongeveer 6 cm)
Trek boven lijnstuk AB 2 cirkelbogen met AB als straal en A en B als middelpunten. Het snijpunt van de cirkelbogen is C.
Trek AC
Hoek ∠CAB is de gevraagde hoek van 60◦
Opmerking: Merk op dat je eigenlijk een gelijkzijdige driehoek hebt geconstrueerd.
Zoals je weet, zijn alle hoeken en alle zijden dan gelijk. De 3 hoeken van een driehoek
zijn samen altijd 180◦ . Dus elke hoek is 60◦ en dat was precies de bedoeling)
9
Een hoek van 45◦
Basisconstructie 9 Constructie van een hoek van 45◦ (op een lijn)
Gegeven: Een willekeurige lijn met daarop een punt P
Constructie beschrijving:
ˆ
ˆ
ˆ
Trek een willekeurige lijn en neem daarop een punt P aan.
Richt in P een loodlijn op volgens basisconstructie nr. 6
Construeer de bissectrice van ∠P volgens basisconstructie nr. 4
Nu is de gevraagde hoek van 45◦ ontstaan.
Opmerking: Merk op dat je eigenlijk een hoek van 90◦ door midden deelt. De deelhoeken zijn dus 45◦
10 Gelijkbenige driehoek
Basisconstructie 10
Constructie van willekeurige gelijkbenige driehoek
Gegeven:
Een willekeurig lijnstuk AB als basis voor de driehoek.
(Neem voor het gemak ongeveer 6cm)
Constructie beschrijving:
ˆ
ˆ
ˆ
ˆ
ˆ
Neem een afstand in de passer, die wat groter is dan de afstand AB.
Trek met A als middelpunt een cirkelboog boven AB
Trek dezelfde cirkelboog met B als middelpunt
Waar beide cirkelbogen elkaar snijden ontstaat punt C
Trek AC en BC
Driehoek ABC is de gevraagde willekeurige gelijkbenige driehoek.
Opdracht:
Voer op de achterkant dezelfde opdracht uit, maar nu met een straal van iets meer
dan de helft van AB. Wat kun je zeggen over hoek C die nu is ontstaan in vergelijking
tot hoek C van de eerste constructie?
11 Zwaartelijn in een driehoek
Basisconstructie 11 Gegeven een driehoek 4ABC. Een zwaartelijn neerlaten op een
de zijde AB vanuit punt C
Een zwaartelijn is een lijn, die van een hoekpunt naar het midden van de overstaande
zijde loopt.
Gegeven:
De driehoek 4ABC
Constructie beschrijving:
ˆ
ˆ
Bepaal met basisconstructie 1 het midden van AB noem dat punt M.
Trek de lijn CM
De lijn CM is de gevraagde zwaartelijn