Actualiteit

Actualiteit
www.rekenhoek.nl
Het tasje van Janneke
Dat telt
4
7 8
Het tasje van Janneke.
In de klas was weer eens een rage ontstaan. Na de vlechtjes in het haar, knikkers, flippo’s, waren er
nu plotseling punnikklosjes. Het ging er om wie de langste draad kon maken. Rekenkundig zat daar
niks uitdagends aan… voor de bovenbouw tenminste niet. We hadden er in de kring al eens over
gesproken: kleurcombinaties, de naaihoek waaruit breigaren verdween als sneeuw voor de zon, het
verschil tussen vingerhaken en punniken.
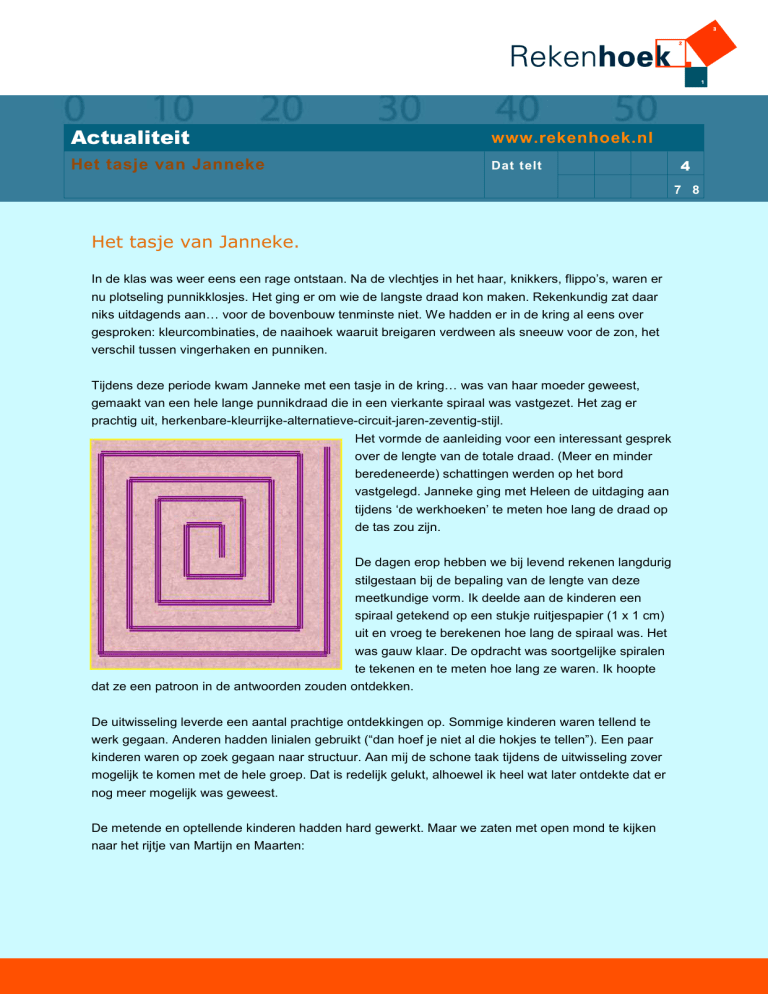
Tijdens deze periode kwam Janneke met een tasje in de kring… was van haar moeder geweest,
gemaakt van een hele lange punnikdraad die in een vierkante spiraal was vastgezet. Het zag er
prachtig uit, herkenbare-kleurrijke-alternatieve-circuit-jaren-zeventig-stijl.
Het vormde de aanleiding voor een interessant gesprek
over de lengte van de totale draad. (Meer en minder
beredeneerde) schattingen werden op het bord
vastgelegd. Janneke ging met Heleen de uitdaging aan
tijdens ‘de werkhoeken’ te meten hoe lang de draad op
de tas zou zijn.
De dagen erop hebben we bij levend rekenen langdurig
stilgestaan bij de bepaling van de lengte van deze
meetkundige vorm. Ik deelde aan de kinderen een
spiraal getekend op een stukje ruitjespapier (1 x 1 cm)
uit en vroeg te berekenen hoe lang de spiraal was. Het
was gauw klaar. De opdracht was soortgelijke spiralen
te tekenen en te meten hoe lang ze waren. Ik hoopte
dat ze een patroon in de antwoorden zouden ontdekken.
De uitwisseling leverde een aantal prachtige ontdekkingen op. Sommige kinderen waren tellend te
werk gegaan. Anderen hadden linialen gebruikt (“dan hoef je niet al die hokjes te tellen”). Een paar
kinderen waren op zoek gegaan naar structuur. Aan mij de schone taak tijdens de uitwisseling zover
mogelijk te komen met de hele groep. Dat is redelijk gelukt, alhoewel ik heel wat later ontdekte dat er
nog meer mogelijk was geweest.
De metende en optellende kinderen hadden hard gewerkt. Maar we zaten met open mond te kijken
naar het rijtje van Martijn en Maarten:
Spiraal Nr
Enkel
Dubbel
Antwoord
Dit komt er bij
1
1
2
2
+4
2
3
6
6
+6
3
6
12
12
+8
4
10
20
20
+10
5
15
30
30
+??
nr. 1
nr. 2
nr. 3
nr. 4
nr. 5
De jongens hadden van binnenuit de lengte geteld, en omdat er telkens 2 stukken waren van dezelfde
lengte hadden ze elk stuk vermenigvuldigd met de factor 2. Ze telden telkens de lengte van een enkel
lijnstuk bij elkaar op. (4 bestaat uit 1 + 2 + 3 + 4 = 10).
Tijdens het gesprek ontdekten we (ik denk dat het vooral door mijn vragen kwam) een merkwaardig
rijtje: er komt telkens het volgende getal uit de rij van de even getallen bij. (Zie de rode getallen in de
tweede kolom).
Maar er was protest: de oorspronkelijke tekening was anders dan Maarten en Martijn voorstelden.
Hun antwoorden waren ook niet juist. De buitenste lijn was niet 2 x maar 3 x getekend. En dan zou het
rijtje echt anders worden. Op het bord kwam:
Spiraal Nr
Buitenste
1
3x1
2
3x2
3
Binnenste totaal
Antwoord
Het rijtje
3
+5
2
8
+7
3x3
6
15
+9
4
3x4
12
24
+ 11
5
3x5
20
35
+ ??
etc
nr. 1
nr. 2
nr. 3
nr. 4
nr. 5
Ook hier ontdekten we een interessant rijtje: een hele rij oneven getallen werd keurig in volgorde
toegevoegd.
Ik wilde graag nog een stap verder komen dan enkel deze rekenontdekking. “Kunnen we nu ook
handig uitrekenen hoe lang de draad op deze tekening is?”, was mijn vraag. Het bleek een station te
ver voor de meeste kinderen. Maarten en Martijn hadden het door. Ook de rest van de week zag ik ze
nog regelmatig tekenen en rekenen aan de spiralen. Ze telden de lengte van de buitenste langste lijn
en maakten dan gebruik van de tabel die we samen hadden bedacht. In hoeverre ze ook de rij
oneven getallen hebben ingezet bij hun rekenwerk kon ik niet meer nagaan. Daarmee zouden ze ten
volle hebben geprofiteerd van onze rekenontdekking.
Later.
Pas later las ik in een brochure van De Freinetbeweging (zie www.freinet.nl) een beschrijving van Jan
Paul Smit over spiralen. De hoofdpersonen gingen in hun denkwerk verder en kwamen ook tot een
formule om de lengte van de totale draad in een spiraal te berekenen. Hun beschrijving voeg ik toe.
“Bianca en Nicole, uit groep 5, hadden met handwerken een lange sliert gehaakt en die wilden ze op
een lapje naaien Het lapje van Bianca was vierkant. Ze had het zo opgespeld. Na een tijdje vroeg
Bianca aan Nicole: “Hoe vaak heb jij al afgehecht?”
Miekee dacht: het is misschien leuk een werkkaart te maken over hoeveel draden je nodig hebt om de
hele spiraal vast te zetten. Je kan dat door meten te weten komen.
Miekee liet het aan Jan-Paul zien en die zei dat je een soort formule zou kunnen maken om de lengte
van de spiraal te weten zonder te meten.
We deden net alsof de afstanden tussen de lijnen telkens één centimeter was. We zetten er cijfertjes
bij. We begonnen van de buitenkant uit.
We ontdekten dat de eerste drie zijden even lang waren, de twee volgende 1 cm. kleiner, de twee
daarop volgende zijden weer 1 cm. kleiner, etc.
Als je begint met een zijde van 7 cm. krijg je dit:
L = 3 x 7 + 2 x ( 6+ 5+ 4+ 3+ 2+ 1),
L is de totale lengte van de spiraal, alles is in cm.
L = 3 x 7 + 2 x ( 6+ 5+ 4+ 3+ 2+ 1 ),
L = 3 x 7 + 2 x ( 3 x 7),
L=9x7
Als je begint met een even getal krijg je zoiets:
L = 3 x 8 + 2 x ( 7+ 6+ 5+ 4+ 3+ 2+ 1 ),
L = 3 x 8 + 2 x ( 3 x 8 + 4 ),
L = 3 x 8 + 6 x 8 + 1 x 8,
L = 10 x 8
We deden het ook met andere getallen.
We ontdekten: L = M x ( M + 2) waarbij M de lengte van de eerste zijde is.
Wat zou er gebeuren als de afstand tussen de lijnen niet 1, maar 2 cm. was?
Uit: Jan- Paul wordt al een goede meester. Studenten in De Freinetbeweging. Jan Paul Smit (niet meer te koop)