Uitwerkingen van de opgaven uit: BASISCHEMIE voor het MLO

Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 1
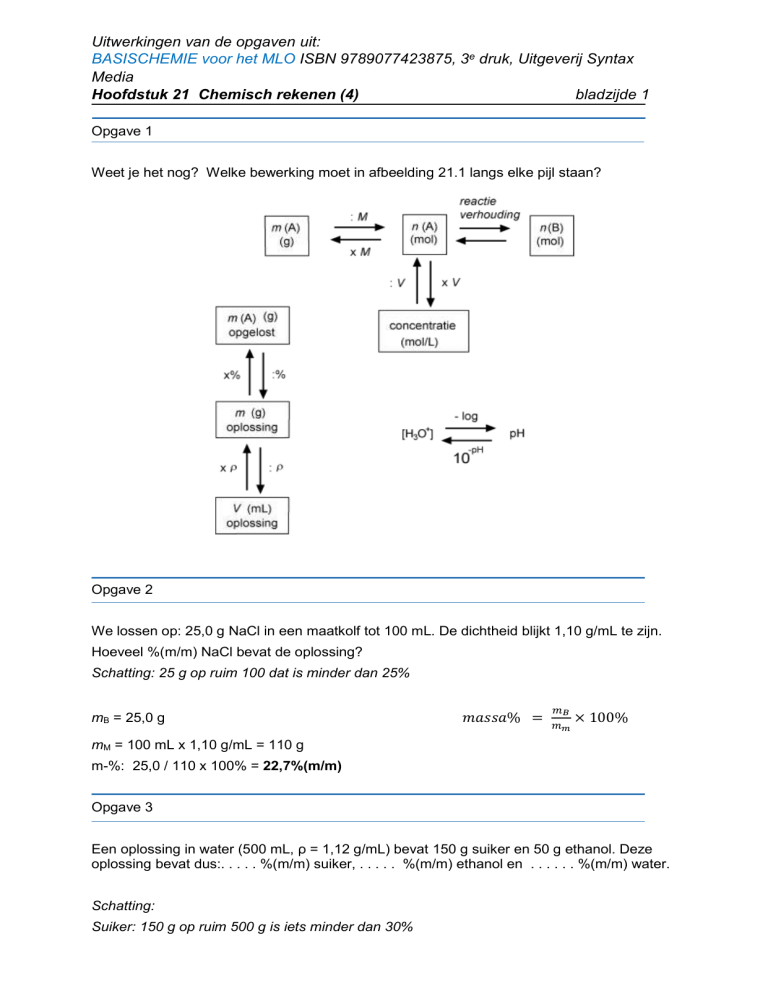
Opgave 1
Weet je het nog? Welke bewerking moet in afbeelding 21.1 langs elke pijl staan?
Opgave 2
We lossen op: 25,0 g NaCl in een maatkolf tot 100 mL. De dichtheid blijkt 1,10 g/mL te zijn.
Hoeveel %(m/m) NaCl bevat de oplossing?
Schatting: 25 g op ruim 100 dat is minder dan 25%
mB = 25,0 g
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
𝑚𝑚
× 100%
mM = 100 mL x 1,10 g/mL = 110 g
m-%: 25,0 / 110 x 100% = 22,7%(m/m)
Opgave 3
Een oplossing in water (500 mL, ρ = 1,12 g/mL) bevat 150 g suiker en 50 g ethanol. Deze
oplossing bevat dus:. . . . . %(m/m) suiker, . . . . . %(m/m) ethanol en . . . . . . %(m/m) water.
Schatting:
Suiker: 150 g op ruim 500 g is iets minder dan 30%
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 2
Ethanol: 50 g op ruim 500 g is iets minder dan 10%
Water: ongeveer 500 g op ruim 500 g is iets minder dan 100%
Massa oplossing: 500 mL x 1,12 g/mL = 560 g
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
𝑚𝑚
× 100%
Suiker: 150 g / 560 g x 100% = 26,8%(m/m)
Ethanol: 50 g / 560 g x 100% = 8,93%(m/m)
water: 100% - 26,8% – 8,93% = 64,3%(m/m)
Opgave 4
Verdun 500 mL zoutoplossing 10 %(m/m) zout (ρ = 1,06 g/mL), met 400 mL water, ρ = 1,00
g/mL).
Hoe groot is het %(m/m) na menging?
Schatting: 10% oplossing wordt verdund van 500 tot 900
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
× 100%
𝑚𝑚
mL dus % wordt ongeveer gehalveerd.
m(opl 1) = 500 mL x 1,06 g/mL = 530 g
m(opl 2) = 400 mL x 1,00 g/mL = 400 g
massa mengsel: 530 + 400 = 930 g
m(zout) = 10% van 530 g = 53,0 g
Nieuw massa-% = 53,0 g / 930 g x 100% = 5,70%(m/m)
Opgave 5
Druivensap bevat 19,2 %(m/m) suiker. De dichtheid van het druivensap is 1,07 g/mL.
a Hoeveel suiker bevat 250 mL van het druivensap?
Schatting: ongeveer 19 g per 100 opl. In 250 mL ≈ 2,5 x 19 ≈ 48 g
𝑑𝑖𝑐ℎ𝑡ℎ𝑒𝑖𝑑
𝜌=
𝑚
𝑉
𝑔
(𝑚𝐿) → 𝒎 = 𝑽 × 𝝆
m(sap) = 250 mL x 1,07 g/mL = 268 g
19,2% suiker is: 0,192 x 268 g = 51,4 g
250 mL sap wordt verdund met 250 mL water (dichtheid water: 1,00 g/mL).
b Hoeveel %(m/m) suiker bevat het verdunde druivensap?
m(verdund sap) = 268 g + 250 g = 518 g
massa-% = 51,4 g / 518 g x 100% = 9,92 g
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
× 100%
𝑚𝑚
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 3
Opgave 6
Stel je maakt 400 mL 18,0 %(m/m) zoutoplossing (dichtheid: 1,17 g/mL) als het zout al 10,0
%(m/m) water bevat.
Hoeveel g water en hoeveel g zout heb je nodig?
Schatting: ongeveer 20% van 400 ≈ 80 g zout maar dan wat meer….
𝑚 = 𝑉×𝜌
m(opl) = 400 mL x 1,17 g/mL = 468 g
m(zout) = 18,0 % van 468 g = 84,2 g droog zout
Het vochtige zout bevat 10,0% water dus 90,0% droog zout. Af te wegen: m(vochtig zout).
dan is:
0,90 x m(vochtig zout) = 84,2 g
► m(vochtig zout) = 84,2 g / 0,90 = 93,6 g
Water nodig: 468 g - 93,6 g = 374,4 g water
Opgave 7
Een analist heeft een ethanol-oplossing die 200 g ethanol per liter bevat.
Hoeveel mL van deze oplossing moet hij nemen om 500 mL te bereiden van een oplossing
die 1,00 %(m/m) ethanol bevat (dichtheid verdunning: 1,00 g/mL)?
Schatting: 200 g / L is ongeveer 20%. Dat moet naar 1%. Dus verdunningsfactor: 20. Nieuw
volume 500 mL / 20 = 25 mL.
Andere redenering: Je hebt nodig: 1,00% van 500 g = 50,0 g ethanol.
1000 mL voorraad-opl. bevat 200 g ethanol. Dat is 0,20 g per 1 mL.
We nemen V mL.
m = V x  ► 50,0 g = V mL x 0,20 g/mL ► V = 25, 0 mL
Opgave 8
600 mL zeewater bevat 3,00 %(m/m) NaCl en heeft een massa van 613 g.
a Hoe groot is de dichtheid van zeewater?
Schatting: iets meer dan 1 g/mL, het is tenslotte water..
 = 613 g / 600 mL = 1,02 g/mL
𝜌=
b Hoeveel g NaCl bevat 1,000 liter zeewater?
M = 1000 mL x 1,02 g/mL = 1020 g ► 3,00 %(m/m) NaCl: 0,03 x 1020 g = 30,7 g
𝑚
𝑉
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 4
c Hoeveel g NaCl bevat 1,000 kg zeewater?
3,00 %(m/m) NaCl: 0,03 x 1000 g = 30,0 g
Opgave 9
Wijn bevat 11,00 %(V/V) ethanol.
Indien 750 mL wijn 66,0 g ethanol bevat, hoe groot is dan de dichtheid van ethanol?
Schatting: ongeveer iets kleiner dan dichtheid van water…
750 mL wijn bevat dan 0,11 x 750 mL = 82,5 mL ethanol
𝜌=
𝑚
𝑉
Dit weegt 66,0 g dus dichtheid: 66,0 g / 82,5 mL = 0,80 g/mL
Opgave 10
Om een ijklijn te maken voor een fotometrische bepaling wordt 500 mg Fe2(SO4)3 afgewogen
en opgelost tot 250,0 mL. Hiervan wordt 10,00 mL verdund tot 1000 mL, hiervan wordt 25,00
mL verdund tot 500 mL.
Van de laatste oplossing wordt resp. 5,0; 10,0; 20,0; en 25,0 mL in kolven van 100 mL
gepipetteerd.
Hoe groot zijn de massaconcentraties Fe2(SO4)3 (in mg/L) na aanvullen?
Schatting: moeilijk te schatten.
Maar voor ijklijnen zijn de massaconcentraties meestal in de orde van 0,1 tot 10 mg/L (ppm).
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 5
De snelste rekenwijze is als volgt:
500 mg oplossen tot 250 mL geeft een massaconcentratie van:
 = 500 mg / 0,25 L = 2000 mg/L
10 mL verdunnen tot 1000 mL, verdunningsfactor 1000 / 10 = 100 x
Nieuwe massaconcentratie:  = 2000 / 100 = 20 mg /L
25 mL verdunnen tot 500 mL, verdunningsfactor 500 / 25 = 20 x
Nieuwe massaconcentratie:  = 20 / 20 = 1 mg /L
5 mL verdunnen tot 100 mL, verdunningsfactor 100 / 5 = 20 x
Nieuwe massaconcentratie:  = 1 / 20 = 0,05 mg /L
Enzovoort. Om het overzichtelijk te houden zin de eenheden en decimalen in de berekening
weggelaten. Maar de eindconcentraties moeten net als de inweeg in 3 cijfers gegeven
worden dus: 0,0500; 0,100; 0,200; 0,250 mg/L
Opgave 11
25,00 mL verdund zoutzuur met c(HCl) = 0,1000 mol/L wordt getitreerd met 22,50 mL NaOH-oplossing (in de buret).
a Hoeveel mmol HCl bevat de 25,00 mL?
𝑛𝐵 = 𝑉 × 𝑐𝐵 ► 25,00 mL x 0,1000 mmol/mL = 2,50 mmol
b Met hoeveel mmol NaOH reageert dit?
Reactie 1 : 1 dus 2,50 mmol HCl reageert met 2,50 mmol NaOH.
c Hoe groot is de sterkte in mol/L van de NaOH oplossing?
𝑛
𝑐(𝐵) = 𝑉 𝐵
𝑀
►
c(NaOH) = 2,50 mmol / 22,50 mL = 0,1111 mmol/mL (mol/L)
Opgave 12
25,00 mL Na2CO3-oplossing wordt getitreerd met een HCl- oplossing met c(HCl) = 0,1000
mol/L, verbruik: 15,00 mL.
Hoeveel mmol Na2CO3 bevat 25,00 mL oplossing?
Reactie:
2 H3O+ + CO32- → 3 H2O + CO2
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 6
𝑛𝐵 = 𝑉 × 𝑐𝐵
► n(HCl) = 15,00 mL x 0,1000 = 1,500 mmol HCl
1,500 mmol HCl reageert met 1 / 2 x1,500 mmol = 0,750 mmol Na2CO3
Opgave 13
5,00 mL H2SO4-oplossing wordt verdund tot 100,0 mL. Hiervan wordt 25,00 mL verdund tot
100 mL. Van de laatste oplossing wordt 10,00 mL getitreerd met een NaOH-oplossing
waarvan c(NaOH) = 0,1000 mol/L. Verbruik: 20,50 mL.
Bereken de analytische concentratie van de oorspronkelijke H2SO4-oplossing.
Globale reactie: H2SO4 + 2 NaOH → Na2SO4 + 2 H2O
De eerste verdunning is 100 / 5 = 20 x
De tweede verdunning is: 100 / 25 = 4 x
Totale verdunning: 20 x 4 = 80 x
𝑛𝐵 = 𝑉 × 𝑐𝐵
► n(NaOH) = 20,50 mL x 0,1000 = 2,050 mmol NaOH
2,05 mmol NaOH reageert met: 1 / 2 x 2,050 mmol = 1,025 mmol H2SO4
𝑛
𝑐(𝐵) = 𝑉 𝐵
𝑀
► c(H2SO4) = 1,025 mmol / 10,00 mL = 0,1025 mmol/mL (mol/L)
Vóór de verdunningen dus: 0,1025 mol/L x 80 = 8,20 mol/L
Opgave 14
10,00 mL H2SO4-oplossing wordt verdund tot 500,0 mL, hiervan wordt 25,00 mL getitreerd
met 38,30 mL NaOH-oplossing, c(NaOH) = 0,1000 mol/L.
Bereken de analytische concentratie van de oorspronkelijke H2SO4-oplossing.
De verdunning is 500 / 10 = 50 x
𝑛𝐵 = 𝑉 × 𝑐𝐵
► n(NaOH) = 38,30 mL x 0,1000 = 3,830 mmol NaOH
3,830 mmol NaOH reageert met: 1 / 2 x 3,830 mmol = 1,915 mmol H2SO4
𝑛
𝑐(𝐵) = 𝑉 𝐵
𝑀
► c(H2SO4) = 1,915 mmol / 25,00 mL = 0,0766 mmol/mL (mol/L)
Vóór de verdunning dus: 0,0766 mol/L x 50 = 3,830 mol/L
Of anders…..:
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 7
25 mL verdunde H2SO4-oplossing bevat 1,915 mmol H2SO4.
In 500 mL van de verdunde oplossing zit: 500 / 25 x 1,915 mmol = 38,30 mmol H2SO4.
Dan bevat 10,00 mL onverdunde opl. dezelfde hoeveelheid.
Concentratie: 38,30 mmol / 10,00 mL = 3,830 mmol/mL (mol/L)
Opgave 15
1,4322 g Na2CO3 wordt afgewogen en opgelost in een maatkolf van 250 mL. Na aanvullen
wordt hieruit 10,00 mL gepipetteerd en getitreerd met 10,99 mL H2SO4-oplossing.
Reactie: CO32- + 2 H3O+ → 3 H2O + CO2
Bereken de analytische concentratie van het zuur.
H2SO4 levert 2 H3O+ hierdoor is de reactieverhouding H2SO4 en Na2CO3: 1 op 1
Hoeveelheid Na2CO3 in mmol: n(Na2CO3) = 1432,2 mg / 106,0 mg/mmol = 13,51 mmol.
Deze hoeveelheid is opgelost in 250 mL. In 10,00 mL van deze oplossing zit dan:
10 / 250 x 13,51 mmol = 0,5405 mmol Na2CO3
Dit reageert met evenveel H2SO4 in 10,99 mL H2SO4-oplossing.
Concentratie H2SO4 dus: 0,5405 mmol / 10,99 mL = 0,0492 mmol/mL
(mol/L)
Opgave 16
Van oxaalzuurdihydraat (formule: ((COOH)2.2H2O) weegt een analist 5050 mg af, hij lost het
op tot 250 mL. Hieruit wordt 10,00 mL gepipetteerd en getitreerd met NaOH. Verbruik: 15,27
mL.
Reactie: (COOH)2 + 2 OH- → (COO)22- + 2 H2O
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 8
Bereken de analytische concentratie van de NaOH-oplossing.
“Titerstelling” de inweeg is zuivere stof. We starten de berekening bij de inweeg.
n(oxaalzuur) = 5050 mg / 126,07 mg/mmol = 40,06 mmol. Opgelost tot 250 mL. 10,00 mL
van deze oplossing bevat dan:
10,00 / 250 x 40,06 mmol = 1,6023 mmol.
Dit reageert met 2 x 1,6023 mmol = 3,205 mmol NaOH.
3,205 mmol NaOH is opgelost in 15,27 mL.
c(NaOH) = 3,205 mmol / 15,27 mL = 0,2099 mmol/mL (mol/L)
Opgave 17
1,700 g natriumoxalaatdihydraat (formule: (COONa)2.2H2O) wordt opgelost tot 250 mL,
hiervan wordt 25,00 mL gepipetteerd en getitreerd met een HCl-oplossing. Verbruik: 25,37
mL.
Reactie: (COO)22- + 2 H3O+ → (COOH)2 + 2 H2O
Bereken de analytische concentratie van het zuur.
“Titerstelling” de inweeg is zuivere stof. We starten de berekening bij de inweeg.
n(natriumoxalaatdihydraat) = 1700 mg / 170,0 mg/mmol = 10,00 mmol. Opgelost tot 250 mL.
25,00 mL van deze oplossing bevat dan:
25,00 / 250 x 10,00 mmol = 1,000 mmol.
Dit reageert met 2 x 1,000 mmol = 2,000 mmol HCl.
2,000 mmol HCl is opgelost in 25,37 mL.
c(HCl) = 2,000 mmol / 25,37 mL = 0,0788 mmol/mL (mol/L)
Opgave 18
Van huishoudazijn wordt 4,00 g afgewogen en overgebracht in een conische kolf. Na
toevoeging van weinig water wordt de inhoud getitreerd met een NaOH-oplossing c(NaOH)
= 0,1000 mol/L. Verbruik: 28,50 mL.
Reactie: CH3COOH + OH- → CH3COO- + H2O
Bereken het massapercentage (CH3COOH) in het monster.
Gehaltebepaling begin met de titratie-uitkomst.
𝑛𝐵 = 𝑉 × 𝑐𝐵 ► n(NaOH) = 28,50 mL x 0,1000 mmol/mL = 2,850 mmol NaOH
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 9
Dit reageert met evenveel azijnzuur (CH3COOH), dus: 2,850 mmol azijnzuur.
𝑚𝐵 = 𝑛𝐵 × 𝑀𝐵 ► m(CH3COOH) = 2,850 mmol x 60,0 mg/mmol = 171,0 mg azijnzuur
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
𝑚𝑚
× 100%
► 171,0 mg / 4000 mg huishoudazijn x 100% = 4,28%(m/m)
Opgave 19
Voor de bepaling van het H3PO4-gehalte van een fosforzuurmonster wordt 2,000 g van het
monster afgewogen en opgelost tot 250 mL. Hiervan wordt 25,00 mL getitreerd met een
NaOH-oplossing, c(NaOH) = 0,5000 mol/L. Verbruik: 6,95 mL.
Reactie: H3PO4 + 2 OH-
→ 2 H2O + HPO42-
Bereken het massapercentage H3PO4 in het monster.
Gehaltebepaling begin met de titratie-uitkomst.
𝑛𝐵 = 𝑉 × 𝑐𝐵 ► n(NaOH) = 6,95 mL x 0,5000 mmol/mL = 3,475 mmol NaOH
Dit reageert met 1 / 2 x 3,475 mmol = 1,738 mmol H3PO4.
25,00 mL van de H3PO4-oplossing bevat dus 1,738 mmol. 250 mL van deze oplossing bevat
dan: 250 / 25 x 1,738 mmol = 17,38 mmol H3PO4
𝑚𝐵 = 𝑛𝐵 × 𝑀𝐵 ► m(H3PO4) = 17,38 mmol x 98,0 mg/mmol = 1702,8 mg H3PO4.
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
𝑚𝑚
× 100%
► 1702,8 mg / 2000 mg monster x 100% = 85,1%(m/m)
Opgave 20
Om het massapercentage NaOH in een mengsel van NaOH en Na2SO4 te meten wordt
10,90 g van het mengsel afgewogen en opgelost tot 500 mL. Hiervan wordt 10,00 mL getitreerd met een zwavelzuur-oplossing, c(H2SO4) = 0,1000 mol/L. Verbruik: 12,50 mL.
Globale reactie: H2SO4 + 2 NaOH → 2 H2O + Na2PO4
Bereken het massapercentage NaOH in het monster.
Gehaltebepaling begin met de titratie-uitkomst.
𝑛𝐵 = 𝑉 × 𝑐𝐵 ► n(H2SO4) = 12,50 mL x 0,1000 mmol/mL = 1,25 mmol H2SO4
Dit reageert met 2 / 1 x 1,25 mmol = 2,50 mmol NaOH.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 10
10,00 mL van de NaOH-oplossing bevat dus 2,50 mmol. 500 mL van deze oplossing bevat
dan: 500 / 10 x 2,50 mmol = 125,0 mmol NaOH
𝑚𝐵 = 𝑛𝐵 × 𝑀𝐵 ► m(NaOH) = 125,0 mmol x 40,0 mg/mmol = 5000 mg NaOH. (5,00 g)
𝑚𝑎𝑠𝑠𝑎% =
𝑚𝐵
𝑚𝑚
× 100%
► 5,00 g / 10,9 g monster x 100% = 45,9%(m/m)
Opgave 21
Voor de bepaling van de analytische concentratie van verdund zoutzuur (de sterkte is ca.
0,1 mol HCl/L), wordt 25,00 mL uit een maatkolf van 500 mL Na2CO3-oplossing gepipetteerd.
Als de laborante ca. 25 mL wil titreren, hoeveel g Na2CO3 moet ze dan afwegen en tot 500
mL oplossen? Dit is een voor-berekening dus: ongeveer.
De laborante wil 25 x 0,1 ≈ 2,5 mmol titreren.
Dat reageert met 1 / 2 x 2,5 mmol = 1,25 mmol Na2CO3
1,25 mmol Na2CO3 zit dan in 25 mL. 500 mL bevat: 500 / 25 x 1,25 mmol = 25 mmol Na2CO3
25 mmol Na2CO3 weegt: 25 mmol x 106 mg/mmol = 2650 mg
Afwegen: circa 2,6 g Na2CO3
Opgave 22
Voor de bepaling van de analytische concentratie van een HCl-oplossing (ca. 0,1 mol/L) op
borax, weegt een analist a g borax (Na2B4O7.10H2O) af, lost dit op en titreert direct:
Reactie: B4O72- + 3 H2O + 2 H3O+ → 4 H3BO3.
Als hij ongeveer 10 mL zoutzuur wil titreren, hoeveel g borax zal hij dan ongeveer afwegen?
Dit is een voor-berekening dus: ongeveer.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 11
De analist wil titreren: 10 x 0,1 = 1,0 mmolHCl.
Dit reageert met 1 / 2 x 1,0 mmol = 0,5 mmol borax.
𝑚𝐵 = 𝑛𝐵 × 𝑀𝐵 ► m(borax) = 0,5 mmol x 381,37 mg/mmol ≈ 191 mg borax.
Opgave 23
De juiste bewerking langs de pijltjes:
Opgave 24
a
Hoe groot is de molaire massa van zuurstof: O2?
2 x 16,0 g/mol = 32,0 g/mol.
b
Hoe groot is de massa van 1 zuurstofmolecuul (gram)?
1 mol zuurstofmoleculen bevat 6,022 x 1023 moleculen. Dus één molecuul weegt:
32,0 g / 6,022 x 1023 moleculen = 5,31  10-23 g
Opgave 25
Hoeveel moleculen én atomen bevinden zich in de onderstaande hoeveelheden?
1 mol bevat 6,022 x 1023 deeltjes (NA)
a
1,00 mmol S
𝑁𝐵 = 𝑛𝐵 × 𝑁𝐴
► 0,0010 mol en bevat: 0,0010 mol x 6,022 x 1023 atomen/mol =
6,02 x 1020 S-atomen.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 12
b
5,00 x 10-4 mol H2 ► 5,00 x 10-4 mol x = 3,01 x 1020 H2 en 6,02 x 1020 H-atomen,
maar alleen als je de moleculen zou splitsen.
c
5,00 mol CO2 ► 5,00 mol x 6,022 x 1023 moleculen/mol = 3,01 x 1024 CO2
en 3,01 x 1024 atomen C en 6,02 x 1024 atomen O.
d
1,00 x10-5 mol H2O► 1,00 x 10-5 mol x 6,022 x 1023 moleculen/mol = 6,02 x 1018
H2O 1,20 x 1019 H-atomen en 6,02 x 1018 O-atomen.
e
10,0 mmol P4
► 10,0 mmol x 6,022 x 1023 moleculen/mol = 6,02 x 1021 moleculen
P4 en (als we de moleculen splitsen): 2,41 x 1022 atomen P.
Opgave 26
a
Hoeveel gram is 5 mol water en 5 mol waterdamp?
De aggregatietoestand is niet belangrijk. 5 mol H2O weegt 5 x 18,0 = 90,0 g
b
Hoeveel moleculen bevinden zich in deze hoeveelheden?
𝑁𝐵 = 𝑛𝐵 × 𝑁𝐴
De aggregatietoestand is niet belangrijk.
5 mol H2O bevat 5 x 6,022 x 1023 = 3,01 x 1024 moleculen
Opgave 27
Hoe groot is de massa (g) van:
a
100 atomen Fe?
1 mol Fe = 55,85 g
1 mol Fe = 6,022 x 1023 atomen
1 atoom Fe heeft dan een massa van: 55,85 g / 6,022 x 1023 atomen = 9,27 x 10-23 g
100 atomen: 100 x 9,27 x 10-23 g = 9,27 x 10-21 g
b
5 • 1010 moleculen NH3?
1 mol NH3 = 17,0 g
1 mol NH3 = 6,022 x 1023 moleculen
1 molecuul NH3 heeft een massa van: 17,0 g / 6,022 x 1023 atomen = 2,82 x 10-23 g
5 • 1010 moleculen: g = 5 • 1010 x 2,82 x 10-23 g = 1,41  10-12 g
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 13
Opgave 28
Bij verwarmen vallen fosformoleculen uit elkaar volgens de reactievergelijking:
P4 → 4 P
Als men uitgaat van 12,4 mg P4, bereken dan:
a
hoeveel mg P gevormd wordt,
De massa is voor en na de reactie hetzelfde: 12,4 mg
b
hoeveel moleculen P4 er voor de reactie zijn,
12,4 mg = 12,4 mg / 124 mg/mmol = 0,100 mmol. 0,000100 mol.
1 mol P4 = 6,022 x 1023 moleculen P4
0,000100 mol = 0,000100 x 6,022 x 1023 = 6,02  1019 moleculen P4
c
hoeveel atomen P er na de reactie zijn.
Na de reactie zijn er 4 x zoveel atomen P als er moleculen P4 waren.
4 x 6,02  1019 atomen P = 2,41  1020 atomen P
Opgave 29
Hoeveel g AlCl3 is nodig om hieruit 1,00 • 1020 ionen Cl- te verkrijgen?
NA = 6,022 x 1023 = 1 mol
𝑁𝐵 = 𝑛𝐵 × 𝑁𝐴 en: 𝑛𝐵 =
𝑁𝐵
𝑁𝐴
► n(Cl-) = 1,00 • 1020 / 6,022 x 1023 = 1,66 x 10-4 mol Cl-
Voor 1,66 x 10-4 mol Cl- is nodig: 1 / 3 x 1,66 x 10-4 mol = 5,54 x 10-5 mol AlCl3
5,54 x 10-5 mol AlCl3 weegt: 5,54 x 10-5 mol x 133,3 g/mol = 7,39 x 10-3 g
Opgave 30
Hoeveel mg Na2SO4 is nodig om hieruit 5,0 • 1018 ionen Na+ te verkrijgen?
𝑁𝐵 = 𝑛𝐵 × 𝑁𝐴 en: 𝑛𝐵 =
𝑁𝐵
𝑁𝐴
► n(Na+) = 5,00 • 1018 / 6,022 x 1023 = 8,30 x 10-6 mol Na+
Voor 8,30 x 10-6 mol Na+ is nodig: 1 / 2 x 8,30 x 10-6 mol = 4,15 x 10-6 mol Na2SO4
4,15 x 10-6 mol Na2SO4 weegt: 4,15 x 10-6 mol x 142,1 g/mol = 5,90 x 10-4 g ► 0,590 mg
Opgave 31
1,00 kg suiker (C12H22O11) bevat suikerkorrels die gemiddeld 2,0 mg per stuk wegen.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 14
a
Hoeveel mol suikermoleculen bevat 1,00 kg suiker?
1,00 kg = 1000 g
𝑛𝐵 =
𝑚𝐵
𝑀𝐵
►
n(suiker) = 1000 g / 342 g/mol = 2,92 mol suikermoleculen
b
Hoeveel mol suikerkorrels bevat 1,00 kg suiker?
1 korrel weegt 0,0020 g, dus in 1000 g: 5,0 x 105 korrels
𝑁
𝑛𝐵 = 𝑁𝐵
𝐴
c
► n(korrels) = 5,0 x 105 / 6,022 x 1023 = 8,30 x 10-19 mol korrels
Hoeveel mol suikermoleculen bevat 1 korrel gemiddeld?
m(korrel) = 0,0020 g 𝑛𝐵 =
𝑚𝐵
𝑀𝐵
►
n(suiker) = 0,0020 g / 342 g/mol = 5,85 x 10-6 mol suikermoleculen
d
Hoeveel suikermoleculen bevat 1 korrel gemiddeld?
1 korrel bevat gemiddeld 5,85 x 10-6 mol suikermoleculen, dat zijn:
5,85 x 10-6 mol x 6,022 x 1023 deeltjes/mol = 3,52 x 1018 suikermoleculen
Opgave 32
Bij een bepaalde druk en temperatuur is de massa van 1,0 L NH3 10,0 g. Hoe groot is de
massa van 10 L O2 onder dezelfde omstandigheden?
10,0 g NH3 = 10,0 g / 17,0 g/mol = 0,588 mol NH3
1,0 L O2 -gas bevat dan ook 0,588 mol, 10 L O2 –gas is dan 10 x 0,588 mol = 5,88 mol O2
5,88 mol O2 heeft een massa van: 5,88 x 32,0 g/mol = 188 g
Opgave 33
Hoeveel g stikstof heeft een gelijk volume als 100 g zuurstof bij dezelfde temperatuur en
druk?
100 g O2 is: 100 g / 32,0 g/mol = 3,125 mol.
In een gelijk volume bevat stikstof dan evenveel moleculen, dus evenveel mol: 3,125 mol.
3,125 mol N2 weegt: 3,125 mol x 28,0 g/mol = 87,5 g
Opgave 34
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 15
Hoe groot is het volume van 1,00 mol waterstofgas als 16,0 g zuurstof bij dezelfde
temperatuur en druk een volume van 13,0 L heeft?
16,0 g O2 = 16,0 g /32,0 g/mol = 0,50 mol. 1,00 mol gas heeft dan een volume van:
1,00 / 0,50 x 13,0 L = 26,0 L.
Waterstof dus ook.
Opgave 35
De dichtheid van stikstof bij bepaalde temperatuur en druk bedraagt 1,27 g/L. Gas X heeft bij
dezelfde temperatuur en druk een dichtheid van 1,83 g/L.
Bereken de molmassa van X.
Schatting: het gas is ongeveer 1,8 / 1,2 x zo zwaar als stikstof 28 ≈ 42 g/mol.
1,00 Liter stikstofgas bevat 1,27 g N2, dat is: 1,27 g / 28,0 g/mol = 0,0454 mol N2.
Ook 1,00 Liter gas X bevat dan 0,0454 mol.
0,0454 mol X weegt 1,83 g, dus 1,00 mol weegt: 1,83 g / 0,0454 mol = 40,3 g/mol
Opgave 36
Van een gas blijkt 1,00 L bij bepaalde temperatuur en druk 3,130 g te wegen. Onder
dezelfde omstandigheden weegt 1,00 L N2: 1,098 g. Bereken de molmassa van het gas.
Schatting: het gas is ongeveer 3 x zo zwaar als stikstof: 3 x 28 = 84 g/mol.
𝑚
1,00 Liter N2 weegt 1,098 g 𝑛𝐵 = 𝑀𝐵 ► nN2 = 1,098 g / 28,0 g/mol = 0,0392 mol N2
𝐵
Gelijke volumes gelijke hoeveelheden in mol, dus ook het andere gas bevat 0,0392 mol in 1
Liter. 0,0392 mol weegt 3,130 g. Dan weegt 1 mol: 3,130 g / 0,0392 mol = 79,8 g/mol
Opgave 37
10 L CH4-gas wordt verbrand tot CO2 en H2O. Hoeveel L zuurstof bij dezelfde temperatuur
en druk, is hier voor nodig?
CH4 + 2 O2 → CO2 + 2 H2O
Gelijke volumes bevatten gelijke hoeveelheden in mol. Je mag de mol-hoeveelheid in de
reactievergelijking daarom ook lezen als volume. Dus 1 Liter CH4 reageert met 2 Liter O2.
Dus 10 Liter CH4 reageert met 20 Liter O2.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 16
Opgave 38
Propaangas reageert als volgt met zuurstof:
C3H8 + 5 O2 → 4 H2O + 3 CO2
Als we 500 mL propaangas willen verbranden, hoeveel mL zuurstof is dan nodig en hoeveel
mL koolstofdioxide ontstaat bij gelijke temperatuur en druk?
Gelijke volumes bevatten gelijke hoeveelheden in mol. Je mag de mol-hoeveelheid in de
reactievergelijking daarom ook lezen als volume. Dus 1 Liter C3H8 reageert met 5 Liter O2.
Je hebt dus nodig: 500 mL x 5 = 2500 mL O2
Er ontstaat: 500 mL x 3 = 1500 mL CO2
Opgave 39
Hoeveel mol (onder standaardomstandigheden) is:
a
1,00 liter O2
22,4 L gas = 1 mol 1,00 L is: 1,00 / 22,4 x 1 mol = 0,0446 mol
b
10,0 liter CO2
10 L is: 10 / 22,4 x 1 mol = 0,446 mol
c
100 liter NH3?
100 L is: 100 / 22,4 x 1 mol = 4,46 mol
Opgave 40
Hoeveel liter (onder standaardomstandigheden) is:
a
1,00 g NH3
𝑚
𝑛𝐵 = 𝑀𝐵 ► 1,00 g / 17,0 g/mol = 0,0588 mol NH3
𝐵
0,0588 mol NH3 heeft een volume van: 0,0588 mol x 22,4 L/mol = 1,32 L
b
5,00 mg HCN-gas
𝑚
𝑛𝐵 = 𝑀𝐵 ► 5,00 mg / 27,0 mg/mmol = 0,1852 mmol HCN
𝐵
0,1852 mmol HCN heeft een volume van: 0,1852 mmol HCN x 22,4 mL/mol = 4,15 mL
► 0,00415 L
c
20,0 kg Cl2?
20,000 g Cl2 / 70,9 g/mol = 282,1 mol Cl2
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 17
282,1 mol Cl2 heeft een volume van: 282,1 mol x 22,4 mL/mol = 6,32 x 103 L
Opgave 41
Hoeveel L NO (onder standaardomstandigheden) ontstaat bij de oxidatie van 100 g Cu met
salpeterzuur volgens:
3 Cu + 8 H3O+ + 2 NO3- → 3 Cu2+ + 2 NO + 12 H2O
𝑛𝐵 =
𝑚𝐵
𝑀𝐵
► 100 g / 63,5 g/mol = 1,57 mol Cu
Uit de reactie van 1,57 mol Cu ontstaat: 2 / 3 x 1,57 mol = 1,05 mol NO.
Dat is: 1,05 mol x 22,4 L/mol = 23,5 L NO
Opgave 42
Hoeveel L NH3 kun je vrijmaken met een overmaat NaOH uit 100 g Mohr's zout
(Fe(NH4)2(SO4)2.6H2O) ?
Fe(NH4)2(SO4)2.6H2O oplossen: Fe2+ + 2 NH4+ + 2 SO42- + 6 H2O
Reactie met NaOH:
𝑛𝐵 =
𝑚𝐵
𝑀𝐵
NH4+ + OH- → H2O + NH3(g)
► 100 g / 392,13 g/mol = 0,255 mol Mohr's zout ► x 2 = 0,510 mol NH3(g)
1 mol gas = 22,4 L
0,510 mol NH3(g) = 0,510 mol x 22,4 L/mol = 11,4 L
Opgave 43
Hoeveel g BaCO3 kun je maximaal neerslaan door 10,0 L CO2 door een oplossing van
Ba(OH)2 te leiden?
Reacties:
CO2 + 2 OH- →
CO32- + H2O
Ba2+ + CO32- → BaCO3↓
10,0 L CO2 = 10,0 L / 22,4 L/mol = 0,446 mol CO2
0,446 mol CO2 levert 0,446 mol CO320,446 mol CO32- reageert met Ba2+ tot 0,446 mol BaCO3.
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 18
0,446 mol BaCO3 weegt 0,446 mol x 197,3 g/mol = 88,0 g
Opgave 44
11,5 g mierezuur wordt verhit en valt daarbij uiteen in H2O en CO volgens:
HCOOH → H2O + CO
Hoeveel L CO ontstaat er?
11,5 g HCOOH = 11,5 g / 46,0 g/mol = 0,25 mol
Er ontstaat ook 0,25 mol CO, dat is een gas: 0,25 mol x 22,4 L/mol = 5,6 L
Opgave 45
Lucht bevat 20,0 %(V/V) zuurstof.
a
Hoeveel L lucht is nodig om 1000 mL ethanol (ρ = 0,80 g/mL, formule: C2H5OH) volledig
te verbranden?
C2H5OH + 3 O2 → 3 H2O + 2 CO2
1000 mL ethanol weegt: 1000 mL x 0,80 g/mL = 800 g.
800 g C2H5OH is: 800 g /46,0 g/mol = 17,4 mol.
17,4 mol C2H5OH reageert met 3 /1 x 17,4 mol = 52,2 mol O2
52,2 mol O2- gas heeft bij standaard-omstandigheden een volume van:
52,2 mol x 22,4 L/mol = 1169 L
1169 L O2 zit in 100 / 20 x 1169 L = 5,8 x 103 L lucht.
b
Hoeveel L lucht is nodig om 1,00 L aardgas (80 %(V/V) methaan (CH4) en 20 %(V/V)
N2) tot CO2 en H2O te verbranden?
Reactie: CH4 + 2 O2 → 2 H2O + CO2
1,00 L aardgas bevat 0,80 x 1,00 L = 0,80 L CH4
Dat is: 0,80 L / 22,4 L/mol = 0,0357 mol CH4
0,0357 mol CH4 reageert met 2 / 1 x 0,0357 mol = 0,0714 mol O2
dat is: 0,0714 mol x 22,4 L/mol = 1,6 L O2
1,6 L is 20%(V/V). 100% lucht:
Opgave 46
100 / 20 x 1,6 L = 8,0 L lucht
Uitwerkingen van de opgaven uit:
BASISCHEMIE voor het MLO ISBN 9789077423875, 3e druk, Uitgeverij Syntax
Media
Hoofdstuk 21 Chemisch rekenen (4)
bladzijde 19
Hoeveel mL waterstofgas en zuurstofgas kan men door middel van elektrolyse verkrijgen uit
1,00 g water?
Reactie: 2 H2O → 2 H2 + O2
1,0 g H2O is 1,0 g / 18,0 g/mol = 0,0556 mol
(55,6 mmol)
Hieruit ontstaat: 2 / 2 x 55,6 mmol = 55,6 mmol H2
► 55,6 mmol x 22,4 mL/mmol = 1,24 x 103 mL H2
55,6 mmol H2O levert 1 / 2 x 55,6 mmol = 27,8 mmol O2
► 27,8 mmol x 22,4 mL/mmol = 622 mL O2