Practicum Flowlab

Practicum Flowlab
Lien Crombé & Mathias Peirlinck
2de bachelor Ingenieurswetenschappen: bouwkunde
12/11/2009
Opgave 1: Stroming over Clark-Y profiel
Invloed van aanvalshoek op fluïdumeigenschappen
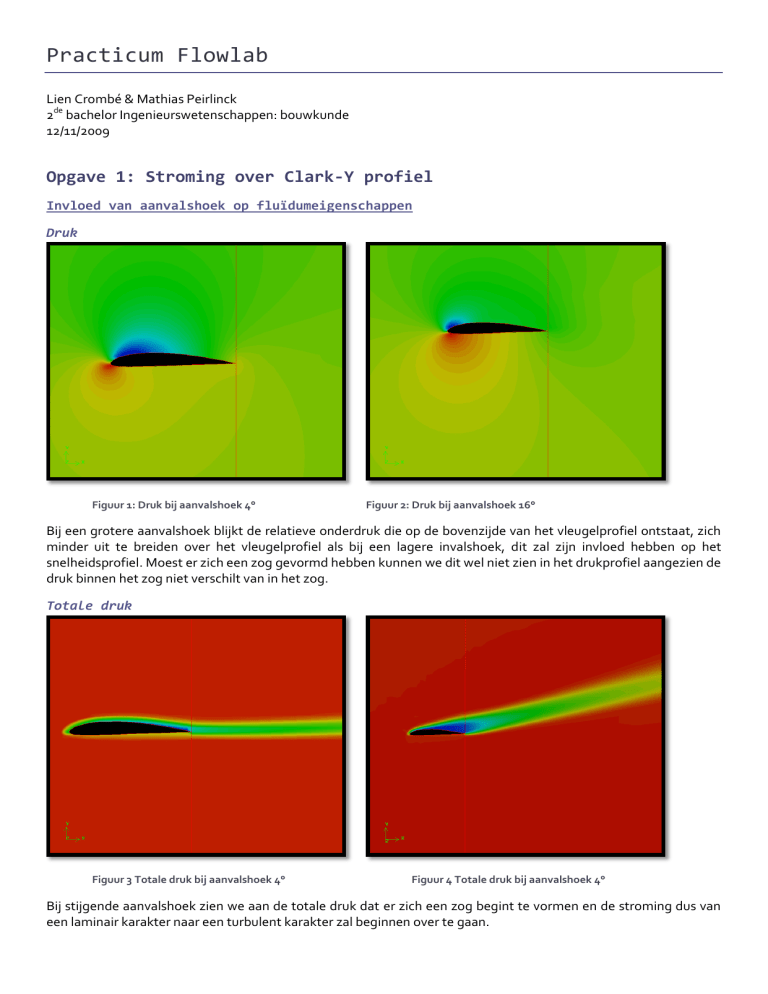
Druk
Figuur 1: Druk bij aanvalshoek 4°
Figuur 2: Druk bij aanvalshoek 16°
Bij een grotere aanvalshoek blijkt de relatieve onderdruk die op de bovenzijde van het vleugelprofiel ontstaat, zich
minder uit te breiden over het vleugelprofiel als bij een lagere invalshoek, dit zal zijn invloed hebben op het
snelheidsprofiel. Moest er zich een zog gevormd hebben kunnen we dit wel niet zien in het drukprofiel aangezien de
druk binnen het zog niet verschilt van in het zog.
Totale druk
Figuur 3 Totale druk bij aanvalshoek 4°
Figuur 4 Totale druk bij aanvalshoek 4°
Bij stijgende aanvalshoek zien we aan de totale druk dat er zich een zog begint te vormen en de stroming dus van
een laminair karakter naar een turbulent karakter zal beginnen over te gaan.
Temperatuur
Figuur 5: Temperatuur bij aanvalshoek 4°
Figuur 6: Temperatuur bij aanvalshoek 16°
Bij lage aanvalshoek heb je geen dissipatie (afscheiding) achter het vleugelprofiel, en blijft de temperatuur
vastzitten in de grenslaag. Bij hoge aanvalshoek krijgen we achteraan de vleugel wervels die zich afscheiden,
waardoor de hogere temperatuur van de grenslaag meegevoerd kan worden in het zog. Ook de kinetische energie
van de wervels werkt deze hogere temperatuur in het zog in de hand.
Snelheid
Figuur 7: Snelheid bij aanvalshoek 4°
Figuur 8: Snelheid bij aanvalshoek 16°
Bij een kleine aanvalshoek krijgen we een vrij standaard stromingsprofiel te zien. Hoe dichter men binnen de
grenslaag bij het vleugelprofiel komt, hoe lager de snelheid. De grote snelheid boven het vleugelprofiel kan men
𝑑𝑃
linken met de lagere druk die daar heerst; als 𝑑𝑥 < 0, zal het fluïdum versnellen. Ten gevolge van de nog kleine
aanvalshoek, zijn er onder de vleugel nog niet al te veel wijzigingen ten opzichte van de omgeving.
Bij een alsmaar grotere aanvalshoek zien we vooraan de bovenzijde van de vleugel weer dezelfde tijdelijke
fluïdumversnelling en daar treden dus de grootste snelheden op. Maar wegens de grotere aanvalshoek ontstaat er
op het einde van het vleugelprofiel een zog aangezien het fluïdum het vleugelprofiel niet langer kan volgen. In dit
zog is de snelheid veel lager dan de aanvankelijke snelheid. De wervels die in het zog gevormd worden sturen het
fluïdum namelijk gedeeltelijk terug waardoor de snelheid binnen het zog veel lager is dan elders. Hierdoor is de druk
in het zog veel hoger zoals we konden zien in figuur 6.Met dit zog en de lagere snelheid binnen dit zog moet bij
luchtvaart zeker rekening gehouden worden want moest bijvoorbeeld de T-staart van een vliegtuig net binnen het
zog van de vleugels komen te liggen, dan wordt de besturing van het vliegtuig sterk bemoeilijkt.
Machgetal
Figuur 9: Machgetal bij aanvalshoek 4°
Figuur 10: Machgetal bij aanvalshoek 16°
Het Machgetal drukt de snelheid van een object uit tegenover de snelheid van het geluid in het medium waardoor
dit object zich verplaatst.
𝑣0
𝑀=
𝑣𝑠
Dus bij de figuren van het machgetal, kunnen we ongeveer dezelfde conclusies trekken als bij de figuren van de
snelheid bij variërende aanvalshoek.
Drukcoëfficient
Figuur 11: Drukcoëfficiënt bij aanvalshoek 4°
Figuur 12: Drukcoëfficiënt bij aanvalshoek 16°
Bij een kleine aanvalshoek zien we dat de grootste positieve drukcoëfficiënt vooraal vooraan het vleugelprofiel
aangrijpt en dan afvlakt naar een positieve constante over de rest van het vleugelprofiel terwijl de negatieve
drukcoëfficiënt ook wel vooraan aangrijpt maar lineair afneemt langsheen het vleugelprofiel. Bij stijgende
aanvalshoeken blijken deze verschijnselen net om te draaien. Merk wel op dat de absolute drukcoëfficiënten bij een
grotere aanvalshoek ook een pak groter zijn. We zien wel dat de lift bij een andere aanvalshoek verschilt. De lift is
namelijk porportioneel met de oppervlakte tussen de onderdruk en de bovendrukcurve.
Wrijvingscoëfficiënt
Figuur 13: Wrijvingscoëfficiënt bij aanvalshoek 4°
Figuur 14: Wrijvingscoëfficiënt bij aanvalshoek 16°
Bij een kleine aanvalshoek vertoont de wrijving boven het vleugelprofiel een mooi parabolisch verloop terwijl de
wrijving onder het vleugelprofiel stijgt om uiteindelijk asymptotisch te naderen tot een bepaalde constante
wrijvingscoëfficiënt.
Bij grotere aanvalshoek, gaan turbulente effecten meespelen waardoor de grote wrijvingscoëfficiënt vooraan de
bovenzijde van het vleugelprofiel plots zeer sterk gaat afnemen terwijl de wrijvingscoëfficiënt op de onderzijde
eerst degressief stijgt en dan weer progressief stijgt.
Lift- en weerstandsverloop in functie van de aanvalshoek
Willen we de invloed van de aanvalshoek bepalen op de lift en de weerstand die het vleugelprofiel ondervindt, dan
berekenen we de lift- en weerstandscoëfficiënten bij enkele aanvalshoeken (Mach = 0,2) en maken we volgende
grafiek.
Aanvalshoek
CL
-4 0,0298533
0
0,38613
4 0,746503
8 0,984318
12
1,03851
16 0,954278
20 0,895827
CD
0,030883
0,01605
0,02309
0,052402
0,109729
0,182407
0,258804
Lift- en weerstandscoëfficiënt
-10
1,2
1
0,8
0,6
CL
0,4
CD
0,2
0
-5
0
5
10
15
20
25
Aanvalshoek (deg)
Blijkbaar is er een bepaalde optimale lift bij een aanvalshoek van 11°, eens we de aanvalshoek nog verder laten
stijgen wordt de lift weer kleiner. De weerstand neemt namelijk alsmaar verder toe omdat het fluïdum alsmaar
loodrechter op het vleugelprofiel invalt.
Als we daarbij de stromingsprofielen bij een zeer grote aanvalshoek ten opzichte van een zeer kleine aanvalshoek
bestuderen, vinden we nog een verklaring voor de dalende lift. Bij een alsmaar grotere aanvalshoek kan het fluïdum
namelijk de bovenzijde van het vleugelprofiel alsmaar minder goed volgen. Dit zien we in volgende 2 figuren.
Figuur 15: Stromingsprofiel bij een aanvalshoek 2°
Figuur 16: Stromingsprofiel bij een aanvalshoek 60°
Stromingspatroon in functie van de Machgetallen
Zoals reeds hierboven gezegd linkt het Machgetal de snelheid van een object in een medium met de
geluidssnelheid in een medium, dus hoe groter het Machgetal, hoe groter de snelheid van het object in het medium.
Bij verschillende Machgetallen (aanvalshoek = 0°) bekomen we volgende isomachcontour-figuren.
Figuur 17: Mach = 0,2
Bij kleine Machgetallen zien we een vrij standaard
stromingsprofiel met hoge Machgetallen boven het
vleugelprofiel, dus daar worden grote snelheden bereikt.
Onder het vleugelprofiel zien we niet zulke grote variatie
in het Machgetal dus daar zal de snelheid een pak lager
liggen als boven het snelheidsprofiel. De grote snelheid
boven het vleugelprofiel kunnen we linken met een veel
lagere druk daar terwijl de lage snelheid onder het
vleugelprofiel gelinkt kan worden met een hogere druk.
Dit drukverschil tussen de onder- en bovenzijde van het
vleugelprofiel zorgt voor de uiteindelijke lift die op het
vleugelprofiel inwerkt, dus in dit geval kunnen we een
grote lift verwachten.
Merk ook op dat de isomachcontouren aan de bovenzijde
mooi parabolisch uitdeinen (dit in tegenstelling tot
hogere Machgetallen, zie verder).
Figuur 18: Mach = 0.5
Ongeveer idem aan Mach = 0.8
Figuur 19: Mach = 0.8
In geval van Mach = 0.8 zien we het parabolisch
uitdeinen van de isomachcontouren niet langer. De
isomachcontouren bevinden zich nu meer naar achteren
op de bovenzijde van het vleugelprofiel en hebben een
eerder lineair verloop. Dit zal duidelijk zijn invloed
hebben op de lift in dit geval die beduidend lager zal
liggen dan bij de lagere Machgetallen. Ook de grotere
wrijving die gepaard gaat met de hogere snelheid zal
een degressieve invloed hebben op de lift.
Figuur 20: Mach = 1.5
Bij Mach = 1.5, beweegt het vleugelprofiel zich door het
medium
met
een
supersonische
snelheid.
Zoals we kunnen zien is het snelheidsverschil tussen
boven- en onderzijde van het vleugelprofiel (die
trouwens weer verder op de achterzijde van het
vleugelprofiel aangrijpen) kleiner dan in de vorige
gevallen, dus de lift die inwerkt op het vleugelprofiel
dankzij het drukverschil tussen boven- en onderzijde zal
weer een pak kleiner zijn dan in de bovenstaande
gevallen. Door de grote snelheid ondervindt het
vleugelprofiel daarbij ook nog eens een ontzettend
grote weerstand waardoor de lift uiteindelijk wel eens
negatief zou kunnen blijken te zijn.
Al deze voorspellingen zien we weerspiegeld in volgende tabel die ons de lift- en weerstandscoëfficiënten bij
verschillende Machgetallen geeft (met aanvalshoek = 0°),
Mach
0,2
0,5
0,8
1,5
CL
0.38613
0.443568
0.652983
-0.0187807
CD
0.0160497
0.0164234
0.0855449
0.122336
Opgave 2: Stroming over een vlakke plaat
Het Nusselt getal is een dimensieloze voorstelling van de convectiecoëfficiënt:
𝑁𝑢𝐿 =
ℎ∗𝐿
𝑘
(1)
Anderzijds weten we ook dat het Nusseltgetal een functie is van het reynoldsgetal Re en het prandtlgetal Pr:
𝑁𝑢𝐿 = 𝑎𝑅𝑒 𝑏 𝑃𝑟 𝑐 (2)
Door gebruik te maken van deze 2 formules, is het mogelijk om de getallen a, b en c te berekenen. Hiervoor hebben
we 3 verschillende numerieke stromingexperimenten uitgevoerd met FlowLab (eerst voor een laminaire stroming
en nadien voor een turbulente stroming). De gegevens van de 3 experimenten vindt u in tabel 1. Door dit
experiment uit te voeren, kregen we steeds een andere waarde voor Q. Met deze waarden zijn we in staat om de
convectiecoëfficiënt h te berekenen met behulp van de volgende formule:
ℎ=
𝑄
𝑚𝑒𝑡 𝛥𝑇 = 100
𝐴 ∗ 𝛥𝑇
Om gebruik te kunnen maken van de eerste formule voor het Nusselt getal, moeten we nu ook nog de thermische
geleidbaarheid k berekenen aan de hand van de volgende formule:
𝑃𝑟 =
𝜇 ∗ 𝑐𝑝
𝑘
Al deze waarden, inclusief het Nusselt getal zijn samengevat in tabel 1.
Re
Pr
Q
h
k
Nu
Experiment 1
100 000
0,7
442,548
4,42548
0,023600784
187,5141
Experiment 2
10 000
0,7
137,711
1,37711
0,023600784
58,3502
Experiment 3
100 000
7
96,227
0,96227
0,0023600784
407,728
Tabel1: Belangrijkste waarden voor een laminaire stroming bij de 3 experimenten
Nu stellen we deze waarden voor het Nusselt getal gelijk aan de tweede vergelijking van het Nusselt getal en zo
hebben we 3 vergelijkingen, waaruit we onze 3 onbekenden a, b en c kunnen halen. Deze zijn voor een laminaire
stroming:



a= 0,6170626133
b=0.5069917505
c=0.3373361120
Wat benaderend overeen komt met Nu = 0.62 Re1/2 Pr1/3 (Dit is hetzelfde resultaat als wat de theorie ons zegt.) .
Nadien hebben we deze 3 experimenten nog eens uitgevoerd voor een turbulente stroming. De belangrijkste
waarden zijn terug te vinden in tabel 2.
Re
Pr
Q
H
K
Nu
Experiment 1
100 000
0,7
1275,22
12,75
0,023600784
540,33
Experiment 2
10 000
0,7
230,09
2,30
0,023600784
97,49
Experiment 3
100 000
7
410,80
4,11
0,023600784
1740,61
Tabel 2: Belangrijkste waarden voor een turbulente stroming bij de 3 experimenten
Op analoge manier bekomen we de volgende waarden voor a, b en c waarmee het Nusselt getal berekend wordt:



a=0.1238430212
b=0.743698088
c=0.50804432053
Nu = 0.12 Re3/2 Pr1/2 (benaderend)
Indien we de bekomen waarden van Q vergelijken, kunnen we concluderen dat turbulentie zorgt voor een veel
grotere warmteoverdracht. En is het dus belangrijk om een turbulente stroming te verkrijgen bij een goede
warmteoverdracht.