13 Golven - Vervoort Boeken

13 Golven
Onderwerpen:
-
Transversale lopende golven
-
Staande transversale golven
-
Longitudinale lopende golven
-
Longitudinale staande golven
-
Toepassingen
13.1 Transversale lopende golven
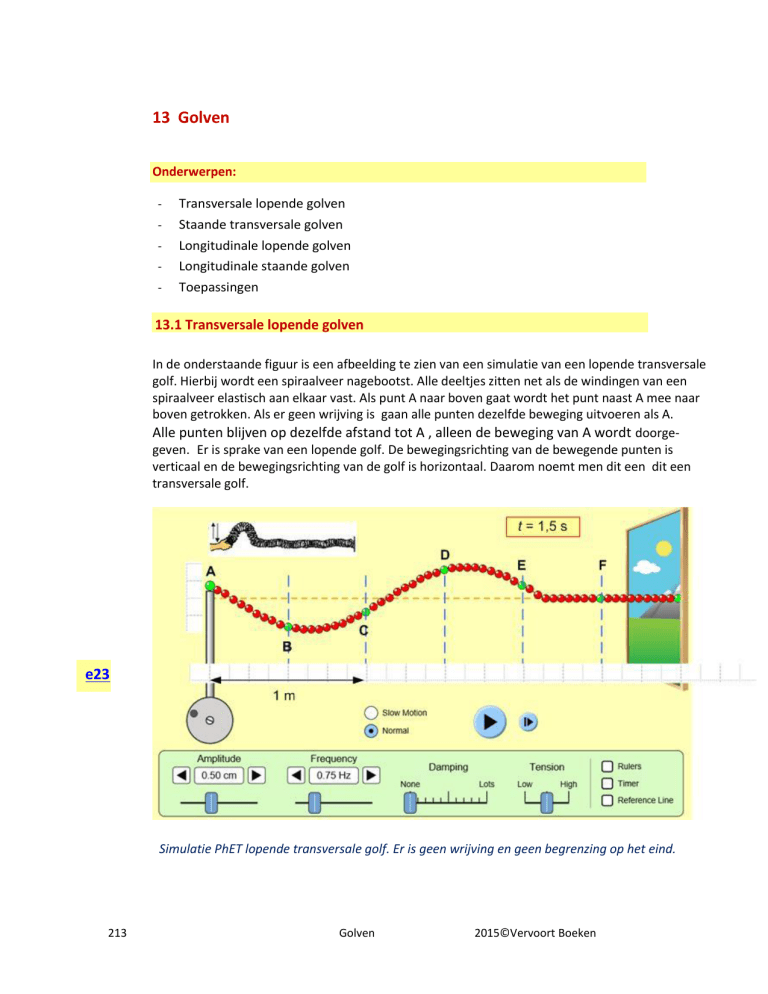
In de onderstaande figuur is een afbeelding te zien van een simulatie van een lopende transversale
golf. Hierbij wordt een spiraalveer nagebootst. Alle deeltjes zitten net als de windingen van een
spiraalveer elastisch aan elkaar vast. Als punt A naar boven gaat wordt het punt naast A mee naar
boven getrokken. Als er geen wrijving is gaan alle punten dezelfde beweging uitvoeren als A.
Alle punten blijven op dezelfde afstand tot A , alleen de beweging van A wordt doorgegeven. Er is sprake van een lopende golf. De bewegingsrichting van de bewegende punten is
verticaal en de bewegingsrichting van de golf is horizontaal. Daarom noemt men dit een dit een
transversale golf.
e23
Simulatie PhET lopende transversale golf. Er is geen wrijving en geen begrenzing op het eind.
213
Golven
2015©Vervoort Boeken
De snelheid van de golf hangt af van de spanning en de massa van de veer. Bij een grotere spanning
wordt de beweging van de windingen(deeltjes) sneller doorgegeven.
Wat is een lopende transversale golf?
Definitie
Een lopende transversale golf is een verstoring (bij veer een verticale beweging) die wordt
doorgegeven en waarbij de snelheid van de verstoring loodrecht staat op de snelheid van de
bewegende deeltjes.
Definitie
De voortplantingssnelheid (v) van een lopende golf is de snelheid waarmee een verstoring wordt
doorgegeven. Bij een echte spiraalveer gaat het dan om enkele meters per seconde.
De snelheid van de deeltjes hangt af van de snelheid en de uitwijking van de deeltjes in verticale
richting. Bij een harmonische trilling is de snelheid in de evenwichtsstand maximaal en deze
maximale snelheid (vmax) hangt af van de frequentie (f) en amplitude (A).
Voorbeeld
We kijken naar de afbeelding hiervoor.
Wat is daar te zien?
1) De golf heeft zich voortgeplant tot iets voorbij punt E (17 schaaldelen) in 1,5 s.
2) Punt E is ongeveer 1 schaaldeel naar boven bewogen.
3) Punt E beweegt naar boven (denk de golf iets verder naar rechts).
4) Punt D gaat naar beneden en heeft zojuist zijn maximale uitwijking (amplitude) gehad.
5) De voorkant van de golf is een ‘berg’ dus alle punten links van de voorkant zijn begonnen met
een beweging naar boven en alle punten rechts van de voorkant gaan beginnen met een
beweging naar boven.
6) Omdat bij één volledige trilling van A één ‘sinus’ in de veer gevormd wordt kun je zien dat A
iets meer dan 1 trilling uitgevoerd heeft.
7) De voortplantingssnelheid van de golf is 17 schaaldelen per 1,5 s
21 m
v  8  1,42 m
s
1,5 s
8) De lengte van 1 ‘sinus’ is 8 schaaldelen = 2 m. Deze lengte noemt men de golflengte (λ).
1
1
 1,33 s
9) De frequentie van de trilling is 0,75 Hz en de trillingstijd T  
f 0,75
10) Punt C heeft iets meer dan een halve trilling uitgevoerd omdat iets meer dan een halve golf
voorbij is. De afstand AC = 1 m = ½ golflengte. Als de golf in A begint op t = 0 s dan duurt het
½ T = 0,62 s voordat de golf bij C is.
Simulatie PhET lopende transversale golf.
De golf voorbij punt C.
214
Golven
2015©Vervoort Boeken
Het u-t-diagram van punt C (grafiek met de uitwijking van C voor verschillende tijdstippen) ziet
er dus als volgt uit:
De uitwijking van punt C op verschillende
tijdstippen.
De eerste 0,62 s is punt C in rust en vervolgens komt de golf voorbij. Punt C gaat eerst naar
boven omdat de voorkant van de golf een ‘bergvorm’op. Bij 1,5 s is C op ongeveer 1 schaaldeel
onder de evenwichtsstand en gaat naar beneden.
Definitie
De golflengte(λ) van een lopende golf is de afstand waarover de golf zich voortplant in één
periodetijd (T). Als het beginpunt een harmonische trilling uitvoert komt de golflengte overeen met
lengte van 1 ‘sinus’ ofwel de afstand tussen twee maxima.
De uitwijking van punt C op verschillende tijdstippen.
Als de voortplantingssnelheid 1,4 m/s bedraagt en de trillingstijd 1,3 s dan geldt:
  1,42 m s  1,33s  1,9 m
Dit klopt ongeveer met de figuur.
Algemeen:
v
  v  T of  
f
215
Golven
2015©Vervoort Boeken
Opgave 13.1
Bij een simulatie van een spiraalveer begint punt A op t = 0 met een harmonische trilling.
De frequentie is 2,0 Hz en de golflengte is 4,0 m. Op een bepaald tijdstip heeft de spiraalveer de
vorm zoals in onderstaande afbeelding te zien is.
De vorm van de veer op een bepaald tijdstip
a)
b)
c)
d)
e)
f)
g)
Hoeveel trillingen heeft beginpunt A uitgevoerd?
Welk tijdstip hoort bij de afbeelding?
In welke richting gaat punt B bewegen?
Leg uit waarom de voortplantingssnelheid gelijk moet zijn aan 8,0 m/s.
Teken het u-t-diagram voor punt E voor de periode tot t = 1 s.
Hoe lang duurt het voordat een golflengte voorbij punt J is.
Leg uit waarom twee punten die een afstand hebben van ½ λ in tegenovergestelde richting
bewegen.
h) Hoe kun je de snelheid van de golf veranderen?
i) Als de trillingstijd van A korter wordt, ofwel de frequentie groter zal de golflengte kleiner
worden. Leg uit waarom dat zo is.
j) Als de maximale snelheid van A minder wordt, wordt de golflengte groter en blijft de
voortplantingssnelheid hetzelfde. Waarom?
Opgave 13.2
Start de simulatie E23.
Stel in : oscillate; no end; damping = none; en spanning(tension) = low; amplitude = 0,75 m;
frequentie = 1 Hz
a) Hoeveel golflengtes komen er op elke plaats per seconde voorbij?
b) Wat zal er met de golflengte gebeuren als de spanning in de veer ‘high’ wordt en geef hier een
verklaring voor.
c) Vervolgens wordt de trillingstijd verkleind tot 0,5 s. Waarom zal de golflengte nu 2x zo klein
worden.
d) Als je amplitude (A) verandert, verandert wel de snelheid van de trillende deeltjes, maar niet de
voortplantingssnelheid. Leg uit.
e) Wat zal er gebeuren als er wrijvingsverliezen (damping) zijn?
e23
216
Golven
2015©Vervoort Boeken
e23
Opgave 13.3
Start simulatie E23
Stel in : manual; no end; damping = none; en spanning(tension) = high; slow motion
a) Hoe zal de verstoring er uitzien als het beginpunt met constante snelheid naar beneden
bewogen wordt en vervolgens met grotere snelheid terug gaat naar het beginpunt.
Maak eerst een schets en controleer vervolgens.
b) Hoe zal het u-t-diagram van een punt in het midden van de veer er uitzien? Maak een schets
en controleer door de beweging van dit punt te bestuderen.
Wat is de fase van een trillend punt en het faseverschil tussen twee trillende punten?
De vorm van de veer op een bepaald tijdstip
Voor de trillende punten in bovenstaande golf geldt:
De fase van punt A is 2 ¼, punt A heeft 2 ¼ trilling uitgevoerd t.o.v. de evenwichtsstand.
De fase van punt J is 0, punt J heeft nog geen trilling uitgevoerd.
Het faseverschil tussen de punten A en B = ¼ , punt A heeft ¼ trilling meer uitgevoerd dan punt B.
 A  2 14
J  0
 A  B  14
Definitie
De fase(φ) van een trillend punt is het aantal trillingen dat uitgevoerd is t.o.v de
evenwichtsstand.
Het faseverschil (Δφ)tussen twee punten is het verschil in aantal uitgevoerde trillingen.
Voorbeeld
In voorgaande afbeelding geldt:
 C  1 3 4  1,75
F 1
 G   J  3 4  0,75 of
 G , F  0,75
Het faseverschil tussen twee punten wordt bepaald door het aantal golflengtes tussen deze
punten. Als de afstand een golflengte is is het faseverschil 1
Bij een afstand van ½ gollengte is het faseverschil ½ .
217
Golven
2015©Vervoort Boeken
Algemeen:
x
 

x is de afstand tussen tw ee punten
 is de golflengte
 is het faseversch il tussen tw ee punten.
Voorbeeld
Door een veer loopt een harmonische golf met een golflengte van 2,0 m
Bereken het faseverschil tussen twee punten die een afstand hebben van 0,50 m.
x 0,50 m
  
 0,25

2m
Wat betekent in fase en tegenfase?
Zie voorgaande afbeelding.
Punt A en punt E zijn in fase, ofwel hebben dezelfde uitwijking en bewegen in dezelfde richting.
Twee punten zijn in fase als de onderlinge afstand gelijk is aan een geheel aantal golflengtes.
Punt B en punt D zijn in tegenfase. B en D hebben een tegengestelde uitwijking en bewegingsrichting.
Twee punten zijn in tegenfase als de onderlinge afstand gelijk is aan een geheel aantal
halve gollengtes.
Opgave 13.4
Lopende golf gaat naar rechts
In bovenstaande afbeelding is een lopende golf te zien. De golglengte is 2,0 m
a) Bepaal de fase van E en C.
b) Bepaal het faseverschil tussen de punten B en C.
c) Teken in de figuur twee punten P en Q die in tegenfase zijn.
d) Teken in de figuur een punt dat in tegenfase is met B.
13.2 Staande tranversale golven
Terugkaatsing en interferentie bij vast uiteinde
Als een lopende golf het eind van de veer bereikt heeft, wordt deze teruggekaatst .
Bij een vast uiteinde vindt een faseverschuiving van ½ plaatst, bij een los uiteinde vindt geen
faseverschuiving plaats.
De heengaande golf en de teruggekaatste golf bepalen samen de uitwijking van de deeltjes.
De resulterende uitwijking van het deeltje is gelijk aan de som van de uitwijking van beide golven.
Dit verschijnsel wordt interferentie genoemd.
In onderstaande afbeelding is een heengaande golf en een teruggekaatste golf te zien.
De teruggekaatste golf is ondergaat bij een vast uiteinde een faseverschuiving van ½ .
218
Golven
2015©Vervoort Boeken
Als de heengaande golf aan de voorkant een ‘berg’ heeft dan heeft de teruggelaatste golf aan de
voorkant een ‘dal’.
e23
1
De eerste golf is teruggekaatst , de tweede loopt naar rechts.
2
1
De golven komen elkaar tegen.
3
De golven werken elkaar tegen (destructieve interferentie) en de deeltjes hebben geen resulterende
uitwijking .Let op: ze hebben wel een verticale snelheid)
4
219
De golven vervolgen hun weg.
Golven
2015©Vervoort Boeken
Terugkaatsing en interferentie bij los uiteinde
Als een lopende golf het eind van de veer bereikt heeft, wordt deze teruggekaatst .
In de afbeelding hierna wordt de golf teruggekaatst bij een los uiteinde.
De teruggekaatste golf is ondergaat hierbij geen een faseverschuiving .
Als de heengaande golf aan de voorkant een ‘berg’ heeft dan heeft de teruggelaatste golf aan de
voorkant ook een ‘berg’.
1
De eerste golf is teruggekaatst , de tweede loopt naar rechts.
2
De golven versterken elkaar tegen (constructieve interferentie) en op de plaats waar de golven
elkaar overlappen is de uitwijking op dat tijdstip 2x zo groot.
3
De golven vervolgen hun weg.
220
Golven
2015©Vervoort Boeken
Terugkaatsing en interferentie van harmonische golf bij vast uiteinde
Als een lopende golf het eind van de veer bereikt heeft, wordt deze teruggekaatst .
e23
1
Het beginpunt heeft een halve trilling uitgevoerd en er is een halve golf gevormd in de veer.
2
Het beginpunt heeft een trilling uitgevoerd en er is een halve golf gereflecteerd.
Heengaande en teruggekaatste golf versterken elkaar.
3
Het beginpunt heeft 1 ½ trilling uitgevoerd en er is een halve golf gereflecteerd rechts en links.
Alle goven versterken elkaar.
221
Golven
2015©Vervoort Boeken
4
Het beginpunt heeft 2 trillingen uitgevoerd en er zijn 4 halve golven die elkaar versterken.
De punten links en rechts staan zijn vast , dit zijn knopen. Het punt in het midden krijgt een
amplitude die steeds groter wordt , dit is een buik.
Theoretisch zou deze amplitude oneindig groot worden. In de praktijk wordt deze amplitude
begrensd doordat er wrijving is of gaat de trillende veer stuk. In dat geval is er sprake van
resonantie-catastrofe.
De resulterende vorm noemt men door zijn beweging een staande golf. Het samengaan van
heengaande en gereflecteerde golven noemt men interferentie.
Als de lengte van de veer precies één halve golflengte is krijg je een staande golf . Er is dan sprake
van resonantie.
Bij een staande golf bewegen alle deeltjes tegelijk door de evenwichtsstand en hebben ze allemaal
hun eigen amplitude. Een buik heeft de maximale amplitude en een knoop geldt A = 0 .
Terugkaatsing en interferentie van harmonische golf bij vast uiteinde bij een hogere frequentie.
Als op de veer een geheel aantal halve golflengtes past ontstaat een staande golf.
De eerst volgende frequentie is dus bij bij een frequentie waarbij 1 golflengte ( 2 halve golflengtes)
op de veer passen.
Deze frequentie noemt men de eerste boventoon.
De laagst mogelijke frequentie voor een staande golf noemt men de grondtoon. In dat geval is de
lengte van de veer precies gelijk aan een halve golflengte.
e23
Het beginpunt heeft 1 trilling uitgevoerd en er is 1 golf gevormd.
222
Golven
2015©Vervoort Boeken
Na terugkaatsing ½ golflengte rechts
Na terugkaatsing 1 golflengte rechts
Na terugkaatsing 1 golflengte rechts
en ½ golflengte links
Na terugkaatsing 1 golflengte rechts
en 1 golflengte links
Na weer een halve periode.
Ontstaan van een staande golf door interferentie bij lengte l = 1 λ
Als de energie die bij het beginpunt wordt toegevoerd door wrijving in warmte omgezet wordt zal
de amplitude van de buikpunten niet verder toenemen.
Staande golf met l =2 · ½ λ op twee tijdstippen.
In de figuur is de staande golf te zien op twee tijdstippen. De punten aan weerszijden van de knoop
bewegen in tegenfase ofwel hebben een faseverschil van ½ .
223
Golven
2015©Vervoort Boeken
Alle punten bewegen tegelijkertijd door de evenwichtsstand en op dat tijdstip is de vorm van de
veer een horizontale rechte lijn.
Voorbeeld
De lengte van de veer in bovenstaande afbeelding is 2,0 m. De frequentie van het beginpunt is
0,17 Hz.
a)Bereken de voortplantingssnelheid van de lopende golf.
b)Bereken de maximale snelheid van een buikpunt bij een amplitude van 0,70 m.
a)   l  2,0 m
  v  T  v    f  2 m  0,17 1s  0,34 m s
b) Bij een harmonische trilling geldt dat de snelheid in de evenwichtsstand maximaal is en gelijk is
aan:
v max 
2A
T
vmax 
2A
 2Af  2  0,70  0,17  0,75 m
s
T
Algemene regel
Bij een staande golf in een veer, koord of snaar geldt
l  n  12 
n  1  l  1 2  grondtoon
n  2  l  2  1 2    eerste boventoon
n  3  l  3  1 2   3 2  tweede boventoon
etc.
n  7  l  7  1 2   7 2  zesde boventoon
224
Golven
2015©Vervoort Boeken
Opgave 13.5
In de afbeelding is de simulatie te zien van een staande golf in een spiraalveer op een tijdstip dat de
uitwijking van de buikpunten maximaal is. De veer is aan beide kanten vastgemaakt.
De veer heeft een lengte van 2,0 m en de frequentie van de trillende punten is 1,50 Hz.
a) Welke boventoon is hier te zien?
b) Schets de vorm van de veer ¼ T later.
c) Schets de vorm van de veer ½ T later.
d) Bereken de voortplantingssnelheid van de lopende golven.
e) Bereken de maximale snelheid van een buikpunt.
Terugkaatsing en interferentie van harmonische golf bij los uiteinde .
Bij een losuiteinde wordt de golf teruggekaatst maar ondergaat geen faseverschuiving.
Het uiteinde zal altijd een buikpunt zijn.
Dit betekent dat de lengte van de veer 1 of meer kwart golflengtes zal zijn.
e23
Staande golf bij l = 1/4 λ bij los uiteinde
225
Golven
2015©Vervoort Boeken
In de voorgaande afbeelding is de staande golf te zien bij de laagst mogelijke frequentie,
de grondtoon. Het meest linkse punt beweegt met zeer kleine amplitude en mag beschouwd
worden als een knoop. Het meest rechtse punt is los en is een buikpunt.
¼ T later zal de vorm een rechte horizontale lijn zijn en ½ T later zal de golf gespiegeld zijn t.o.v de
horizontaal.
Staande golf bij l = 3/4 λ De eerste boventoon.
Staande golf bij l = 5/4 λ De tweede boventoon.
In het algemeen geldt:
l  (2n  1)  1 4 
n  1  l  1 4  grondtoon
n  2  l  3  1 4   3 4  eerste boventoon
n  3  l  5  1 4   5 4  tweede boventoon
etc.
n  5  l  9  1 4   9 4  vierde boventoon
226
Golven
2015©Vervoort Boeken
Opgave 13.5
In de afbeelding is de simulatie te zien van een staande golf in een spiraalveer op een tijdstip dat de
uitwijking van de buikpunten maximaal is. De veer heeft aan de rechterkant een los uiteinde.
De veer heeft een lengte van 2,0 m en de frequentie van de trillende punten is 0,12 Hz.
a) Bereken de golflengte
b) Bereken de voortplantingssnelheid van de lopende golven.
c) Wat zal er gebeuren als je de veer bij het knooppunt vast zet.
d) Schets de vorm van de veer bij de derde boventoon.
e) Welke frequentie hoort bij de derde boventoon.
13.3 Longitudinale lopende golven
Een spiraalveer met platte windingen ,een‘slinky’, is erg geschikt om longitudinale golven te
bestuderen.
Bij longitudinale- of lengtegolven is de trillingsrichting van de deeltjes hetzelfde als de
voortplantingssnelheid.
Longitudinale en transversale golf.
227
Golven
2015©Vervoort Boeken
Longitudinale golf
Transversale golf
Als de veer naar rechts bewogen wordt en
weer terug ontstaat er een verdichting die
naar rechts loopt.
Als de veer omhoog bewogen wordt en weer terug
ontstaat er een berg die naar rechts loopt.
Als de veer vervolgens naar links bewogen
wordt en weer terug ontstaat er een
verdunning die naar rechts loopt.
Als de veer vervolgens naar beneden bewogen
wordt en weer terug ontstaat er een dal dat naar
rechts loopt.
Bij een harmische trilling aan het begin loopt
er een harmonische golf naar rechts die
bestaat uit een reeks verdichtingen en
verdunningen.
Bij een harmonische trilling aan het begin ontstaat
er een harmonische golf naar rechts die bestaat
uit een rechts bergen en dalen.
De meest voorkomende longitudinale golf is de geluidsgolf in lucht.
Als je lucht samendrukt wordt de drukverhoging doorgegeven zoals de verdichting in de slinky.
Longitudinale golf in een slinky is analoog aan een lopende golf in een luchtkolom
Een trillend membraam, zoals gebruikt in een luidspreker, zorgt afwisselend voor een
drukverhoging en een drukverlaging. De drukverhoging is een gevolg van een grotere dichtheid van
de luchtmoleculen t.o.v de gewone luchtdruk. Een drukverlaging is het gevolg van een lagere
dichtheid van de luchtmoleculen.
228
Golven
2015©Vervoort Boeken
De snelheid waarmee de verandering in druk wordt doorgegeven is gelijk aan de gemiddelde
snelheid van de moleculen. Bij 20 0C is dat 340 m/s, de geluidssnelheid.
Drukveranderingen met een frequentie tussen 20 Hz en 20.000 Hz nemen we waar als geluid.
Het oor heeft een zeer breed bereik van drukgevoeligheid. Drukveranderingen van 2·10-5 Pa
(0 dB) tot 20 Pa (120 dB) zijn waarneembaar.
Wat zien we in onderstaande afbeelding ?
Grafiek 2
Een longitudinale golf door een luchtkolom. Alle punten blijven op hun plaats en trillen om de
evenwichtsstand in horizontale richting. Daardoor lopen er verdichtingen en verdunningen door de
lucht
De deeltjes links van B gaan op dit tijdstip naar rechts en de deeltjes tussen B en D gaan naar links,
waardoor in punt B een verdichting van de lucht ontstaat. De deeltjes bij A hebben de maximale
uitwijking naar rechts. De deeltjes bij punt C hebben de maximale uitwijking naar links.
De deeltjes links van D gaan naar links en de deeltjes rechts van D gaan naar rechts, waardoor in
punt D een verdunning van de lucht ontstaat. De verdichtingen en verdunningen lopen naar
rechts.
Grafiek 1
Dit is een schematische weergave van de gemiddelde uitwijking van de deeltjes op een bepaald
tijdstip. Hier is de gemiddelde uitwijking van de luchtdeeltjes uitgezet tegen de plaats.
De uitwijking naar rechts is naar boven uitgezet en de uitwijking naar links is naar beneden
uitgezet. Je kunt hierin beter zien welke uitwijking de deeltjes hebben. Bij punt A hebben de
deeltjes een maximale uitwijking naar rechts en deeltje C de maximale uitwijking naar links.
Bij punt B is er geen uitwijking, hier is een verdichting gevormd.
Als het linkerdeeltje blijft trillen in horizontale richting gaan de verdichtingen en verdunningen door
de lucht naar rechts.
Longitudinale golf in een luchtkolom. Verdichtingen en verdunningen gaan door een
luchtkolom en deze kun je schematisch weergeven met een ‘sinusgolf ‘.
229
Golven
2015©Vervoort Boeken
Grafiek 3 en 4
Op de plaats waar een verdichting zit is de dichtheid (ρ) van de lucht iets groter en de druk iets
groter dan de luchtdruk(Δp = +). Op de plaats waar een verdunning zit van de lucht is de dichtheid
van de lucht iets lager en de druk van de lucht iets lager dan de luchtdruk(Δp = -). Er gaan door de
luchtkolom gebiedjes met hogere en lagere drukken lopen. Als het beginpunt een trilling
uitgevoerd heeft is er een golflengte gevormd. De golflengte is de afstand tussen twee punten met
dezelfde uitwijking en ook de afstand tussen twee punten met dezelfde drukverhoging of
drukverlaging. De plaats van de verdichting ligt altijd op de plaatsen waar de deeltjes geen
uitwijking hebben en op het punt staan naar rechts te gaan (punt B). De plaats van de verdunning
ligt op de plaats waar de deeltjes geen uitwijking hebben en naar links gaan (D).
Een longitudinale golf in een gas wordt ook wel een drukgolf genoemd.
e24
Klik op hyperlink e24 om een simulatie te bekijken van een lopende geluidsgolf.
Simulatie door Dan Russell van een lopende longitudinale drukgolf. De deeltjes trillen
om een bepaalde plaats en horizontale richting en de verdichtingen en verdunningen
lopen naar rechts.
compression = verdichting en rarefaction = verdunning
Opgave 13.6
Door middel van een stemvork worden geluidsgolven gevormd (zie afbeelding).
De snelheid van de geluidsgolven is 340 m/s.
a) Welke grootheid kun je aflezen uit de sinusvormige grafiek?
b) Bereken de afstand tussen twee plaatsen met maximale drukverhoging bij een toon van 400
Hz.
c) Schets in het diagram de sinus waarin de gemiddelde uitwijking van de luchtdeeltjes is af te
lezen op verschillende plaatsen.
230
Golven
2015©Vervoort Boeken
Opgave 13.7
In onderstaande afbeelding van een buis te zien hoe de druk in een buis verandert dooradat er een
geluidsgolf doorheen loopt.
Op de plaatsen waar de lucht is samengeperst wordt uiteraard een hogere druk gemeten.
De grafiek op de achtergrond geeft de uitwijking van de deeltjes op verschillende plaatsen. De
grafiek op de voorgrond geeft luchtdrukverandering aan. De afstand AB is 20 cm.
a) In welke richting bewegen de luchtmoleculen tussen B en C en tussen C en D volgens het
schema van de lopende golf ? Leg uit
b) Waarom is de druk bij B maximaal?
c) Waarom is de druk bij A minimaal?
d) Hoe groot is de gemiddelde uitwijking bij C?
e) Bereken de frequentie van het trillende membraam.
231
Golven
2015©Vervoort Boeken
13.3 Longitudinale staande golven in een ronde pijp
Net zoals bij de transversale lopende golven worden ook de longitudinale golven gereflecteerd bij
het uiteinde van een buis. Heengaande en teruggekaatste golven versterken elkaar en doven elkaar
uit bij bepaalde golflengtes.
Terugkaatsing bij dicht en open uiteinde
Bij een dichtuiteinde kunnen de deeltjes niet horizontaal bewegen en ontstaat altijd een
deeltjesknoop en dus een drukbuik.
Bij een open uiteinde kunnen de deeltjes maximaal bewegen en ontstaat altijd een deeltjesbuik en
dus een drukknoop.
Muziekinstrumenten zoals de fluit en klarinet zijn toepassingen van staande golven in een pijp.
Grondtoon en boventonen bij een pijp die aan beide zijden open is (fluit)
l  n  12 
n  1,2,3.......
Staande golven in een pijp die aan beide kanten open is (fluit).
Bij de grondtoon zijn de deeltjesbuiken en knoop aangegven.
Opgave 13.8
De fluit is 60 cm lang.
Bereken de frequentie die hoort bij de tweede boventoon.
232
Golven
2015©Vervoort Boeken
Grondtoon en boventonen bij een pijp die aan een kant dicht is (clarinet)
l  (2n  1)  1 4 
n  1,2,3.......
Staande golven in een pijp die aan een kant open is (clarinet).
Bij de grondtoon zijn de deeltjesbuiken en knoop aangegeven.
e25
Zie site e25 en kies dan voor play 8.5 om een simulatie te zien van de fluit en clarinet.
Opgave 13.8
Bereken de frequentie van de tweede boventoon bij een fluit.
Opgave 13.9
Bereken de frequentie van de derde boventoon bij een clarinet.
233
Golven
2015©Vervoort Boeken