IJkingstoets burgerlijk ingenieur september 2016

IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 1
IJkingstoets burgerlijk ingenieur september 2016: algemene feedback
Positionering ten opzichte van andere deelnemers
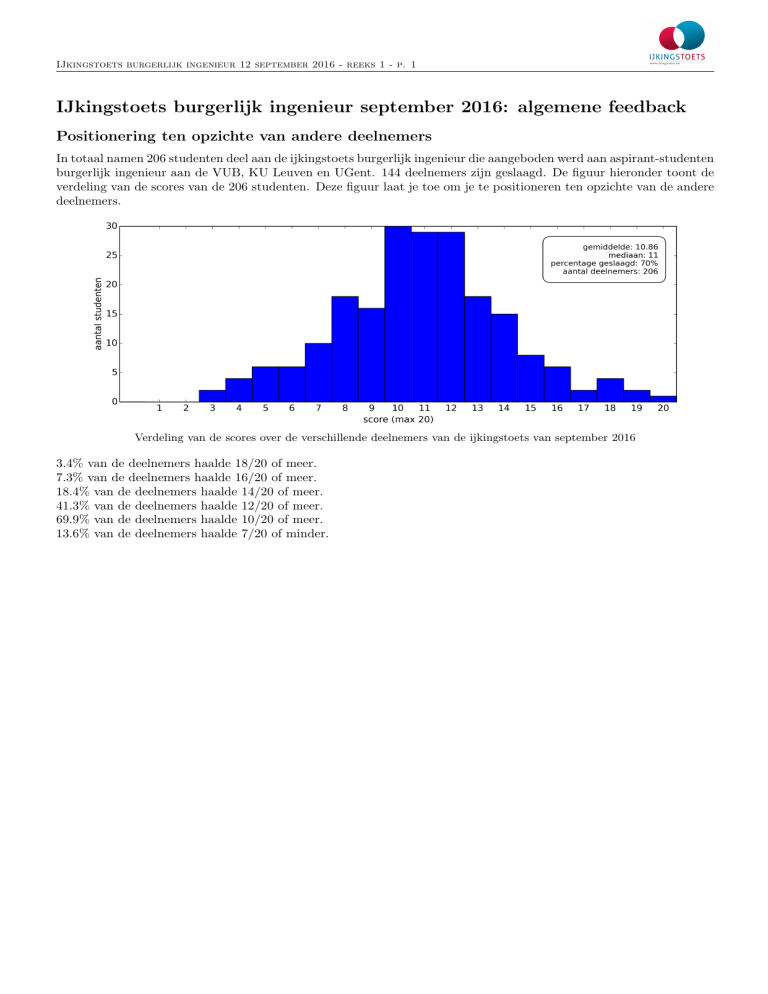
In totaal namen 206 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden werd aan aspirant-studenten
burgerlijk ingenieur aan de VUB, KU Leuven en UGent. 144 deelnemers zijn geslaagd. De figuur hieronder toont de
verdeling van de scores van de 206 studenten. Deze figuur laat je toe om je te positioneren ten opzichte van de andere
deelnemers.
Verdeling van de scores over de verschillende deelnemers van de ijkingstoets van september 2016
3.4% van de deelnemers haalde 18/20 of meer.
7.3% van de deelnemers haalde 16/20 of meer.
18.4% van de deelnemers haalde 14/20 of meer.
41.3% van de deelnemers haalde 12/20 of meer.
69.9% van de deelnemers haalde 10/20 of meer.
13.6% van de deelnemers haalde 7/20 of minder.
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 2
Vervolgtraject voorbije edities
Heel wat van de deelnemers aan de ijkingstoets zijn aan de opleiding bachelor in de ingenieurswetenschappen (KU
Leuven, UGent, VUB) of bachelor in de ingenieurswetenschappen: architectuur (KU Leuven) gestart. De figuur
hieronder toont de studentenstroom tot na de januari-examens. Deze figuur toont dat de wiskundige voorkennis
gemeten tijdens de ijkingstoets, een belangrijke factor is voor je toekomstige studiesucces. Bij de groep die slaagde
op de ijkingstoets heeft een aanzienlijk deel na de januari-zittijd een hoge studie-efficiëntie (groene stroom). Van
studenten uit de groene stroom weten we dat ze bijna allemaal hun bachelor in drie jaar zullen behalen. Een goede
ijkingstoetsscore is echter geen garantie op succes in de opleiding. Hard werken, een goede studieaanpak en motivatie
blijven heel belangrijk! Voor studenten die niet slaagden op de ijkingstoets blijkt het heel moeilijk te zijn om het
bijspijkeren van de voorkennis te combineren met hun studie. Meer dan de helft van de vroegere deelnemers is ofwel al
gestopt met de opleiding in de loop van het eerste semester (zwarte stroom) of heeft een zeer lage studie-efficiëntie in
januari (rode stroom). Van studenten uit de rode stroom weten we dat het heel moeilijk zal zijn om het bachelordiploma
ingenieurswetenschappen te behalen.
Vervolgtraject van de deelnemers aan de voorbije edities van de ijkingstoets. Hierbij is CSE of sudie-efficiëntie in januari het
percentage aan behaalde credits ten opzichte van het aantal opgenomen credits.
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 3
Signalen uit het secundair onderwijs
Vanuit het secundair onderwijs heb je ook heel wat waardevolle signalen gekregen die je kunnen ondersteunen bij
je studiekeuze. Het advies van de klassenraad en het percentage wiskunde behaald in het secundair onderwijs zijn
factoren die samen met de score op de ijkingstoets je een zicht kunnen geven op je toekomstig studiesucces. De figuur
hieronder toont hoe het advies van de klassenraad en het percentage wiskunde uit het secundair samenhangt met
studiesucces in de opleiding voor de huidige generatie eerstejaarsstudenten. De kleurschaal geeft aan welk percentage
in deze groep meer dan 30% van de credits uit het eerste semester behaald heeft.
Mooie resultaten wiskunde én een positief advies van de klassenraad voor ingenieurswetenschappen zijn positieve
signalen voor toekomstig studiesucces. Studenten met een lagere score op wiskunde in het secundair onderwijs of die
een negatief advies van de klassenraad kregen, bevinden zich in de gearceerde rechthoek. Deze groep bevat relatief
weinig studenten die in het eerste semester meer dan 30% van de credits behaald hebben.
Verband tussen het advies van de klassenraad, het percentage wiskunde uit het secundair onderwijs en studiesucces in het
eerste semester van de opleiding burgerlijk ingenieur bij 401 eerstejaarsstudenten academiejaar 2015-2016. De oppervlakte van
elke bol is evenredig met het aantal studenten uit de subgroep. De kleurschaal geeft aan welk percentage in de subgroep meer
dan 30% van de credits uit het eerste semester behaald heeft.
Wij zijn geı̈nteresseerd in uw mening!
Nam u deel aan deze ijkingstoets? Dan zouden we willen vragen om uw mening over dit feedback-document met ons
te delen via deze link.
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 4
Juiste antwoorden en statistieken per vraag
Hieronder staan de vragen, met telkens het juiste antwoord, het percentage dat deze vraag juist heeft beantwoord en
het percentage dat deze vraag heeft blanco gelaten.
Oefening 1
Voor een natuurlijk getal k 6= 0 noteren we met k! het product van de natuurlijke getallen van k t.e.m. 1:
k! = k · (k − 1) · (k − 2) · . . . · 2 · 1 .
Zo is bijvoorbeeld 6! = 6 · 5 · 4 · 3 · 2 · 1.
Wat is het laatste cijfer van
(A) 2
(23527)!
?
(23525)!
(B) 5
(C) 6
(D) 7
Oplossing: A
juist beantwoord: 89 %
blanco: 2 %
Oefening 2
Bestudeer de onderstaande beweringen over rechten en vlakken in de driedimensionale ruimte en ga na of ze algemeen
waar zijn.
• bewering 1: Als de rechte r en de rechte s evenwijdig zijn met het vlak v, dan zijn r en s ook onderling evenwijdig.
• bewering 2: Als twee rechten loodrecht staan op hetzelfde vlak v dan zijn ze evenwijdig.
(A) Geen enkele bewering is juist.
(B) Beide beweringen zijn juist.
(C) Bewering 1 is juist, bewering 2 is fout.
(D) Bewering 1 is fout, bewering 2 is juist.
Oplossing: D
juist beantwoord: 86 %
blanco: 1 %
Oefening 3
Een kinderzwembad heeft een vlakke, horizontale bodem met een oppervlakte van 4 m2 en met loodrecht opstaande
wanden. Het zwembad wordt gevuld met water met een debiet van 20 `/min. Hoe snel stijgt de hoogte van het water
in het zwembad?
(A) 0.5 cm/min
(B) 1 cm/min
(C) 2 cm/min
(D) 4 cm/min
Oplossing: A
juist beantwoord: 87 %
blanco: 8 %
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 5
Oefening 4
Beschouw de veelterm p(x) = (x + a)(x − a)(x − c) in x ∈ R, en a > b > c > 0. Welke van onderstaande uitspraken is
geldig?
(A) p(b) < p(c) < p(0)
(B) p(0) < p(b) < p(c)
(C) p(c) < p(0) < p(b)
(D) p(c) < p(b) < p(0)
Oplossing: A
juist beantwoord: 80 %
blanco: 2 %
Oefening 5
Onderstaande figuur geeft de grafiek van de functie f : R → R weer met een volle lijn en de grafiek van de functie
g : R → R met een streepjeslijn. Welk van onderstaande uitspraken is geldig?
f (x)
3a
2a
(A) f (x) = g(x) + 2a
(B) f (x) = 2g(x) + a
g(x)
a
(C) f (x) = 3g(x)
(D) f (x) = 3g(x) + 2a
x
0
−a
Oplossing: B
juist beantwoord: 61 %
blanco: 2 %
Oefening 6
Hoeveel verschillende oplossingen in C heeft de vergelijking z 4 = 16?
(A) 1
(B) 2
Oplossing: C
juist beantwoord: 49 %
blanco: 15 %
(C) 4
(D) oneindig veel
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 6
Oefening 7
(x + 5)(x2 + 1)
.
x→−5 x2 + 12x + 35
Ga na of volgende limiet bestaat en bereken desgevallend: lim
(x + 5)(x2 + 1)
x→−5 x2 + 12x + 35
De limiet lim
(A) bestaat en is gelijk aan 0.
(B) bestaat en is gelijk aan 13.
(C) bestaat en is gelijk aan +∞.
(D) bestaat niet.
Oplossing: B
juist beantwoord: 74 %
blanco: 6 %
Oefening 8
Vier teams spelen een GPS-spel. Het speelveld kunnen we benaderen door een plat vlak. We voeren een cartesiaans
assenstelsel Oxy in zodat we de positie van elk team kunnen vastleggen met behulp van zijn coördinaat. Team rood
bevindt zich op positie (−1, 0), team groen op (2, −1), team blauw op (2, −2) en team geel op (2, 3). Elk team beschikt
over een GPS-toestel dat geobserveerd wordt door drie satellieten. Elke satelliet localiseert het GPS-toestel binnen
een cirkel op het speelveld. Welk team bevindt zich binnen volgende drie cirkels?
C1 : (x − 1)2 + (y − 3)2 = 25
C2 : x2 + y 2 = 9
C3 : (x − 3)2 + (y − 1)2 = 16
(A) team rood
(B) team groen
(C) team blauw
(D) team geel
Oplossing: B
juist beantwoord: 80 %
blanco: 7 %
Oefening 9
Gegeven is de functie f met voorschrift
(
x als x ≥ 0
f : R → R : x 7→ y =
0 als x < 0
en de functie g met voorschrift
g : R → R : x 7→ y = f (1 + x) + f (1 − x)
Bepaal het minimum van de functie g.
(A) -1
(B) 0
Oplossing: D
juist beantwoord: 41 %
blanco: 25 %
(C) 1
(D) 2
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 7
Oefening 10
Hieronder 4 gevelzichten.
De letters (A) tot (D) geven telkens twee objecten aan. Van elk object zijn er twee gevelzichten waarvan de kijkrichtingen loodrecht op elkaar staan. Geef de letter van de twee objecten waarvan de gevelzichten gegeven zijn.
(A)
(B)
(C)
(D)
Oplossing: C
juist beantwoord: 87 %
blanco: 7 %
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 8
Oefening 11
Beschouw het vlak met cartesiaans assenstelsel xy met de x-as horizontaal naar rechts en de y-as verticaal naar boven.
Hieronder worden alle hoeken gemeten vanaf de positieve x-as. We gebruiken de conventie dat hoeken in tegenwijzerzin
positief zijn. De vector ~a heeft een lengte 1 en maakt een hoek van 10◦ met de positieve x-as. De vector ~b heeft ook
een lengte 1 en maakt een hoek van 40◦ met de positieve x-as. Welke hoek maakt de vector ~a + ~b met de positieve
x-as?
(A) 25◦
(B) 30◦
(C) 40◦
(D) 50◦
Oplossing: A
juist beantwoord: 62 %
blanco: 14 %
Oefening 12
Veronderstel dat x en y complexe getallen zijn die voldoen aan het stelsel
x + (1 − i)y
= 2
(1 − 2i)x + 2y = −1 + 2i,
waarbij i2 = −1. Bepaal x.
(A) 1
(B) −i
Oplossing: B
juist beantwoord: 53 %
blanco: 35 %
(C) −1 − i
(D) −1 + i
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 9
Oefening 13
Een reclamebord heeft een breedte van 4m en een hoogte van 2m. Het bord is met twee kabels opgehangen in het
midden tussen twee verticale kolommen, die 12m uit elkaar opgesteld staan. Op elke kolom i loopt de kabel van een
takel Ti (op hoogte 1.5m boven de fundering) naar de katrol Ki , die op het bovenuiteinde van de kolom is gemonteerd.
Van de katrol loopt de kabel verder naar het hoekpunt van het reclamebord, zoals aangegven op de figuur. De kabel
is strak gespannen. Elke kolom i heeft een hoogte van 10m en is vast verankerd in een fundering in het punt Fi .
De breedte van de kolommen mag verwaarloosd worden, en dus gelijk aan 0 genomen worden. Ook de takels en de
katrollen hebben verwaarloosbaar kleine afmetingen. De vrije hoogte H tussen de onderrand van het bord en de
fundering is instelbaar tussen 0m en 7.5m. De instelling gebeurt door de kabels met behulp van de takels op te rollen,
waarbij ervoor gezorgd wordt dat de lengte van het niet opgerolde deel van de beide kabels tussen de takel en het
aanhechtingspunt op het bord steeds even groot is. Op een bepaald ogenblik is deze lengte van het niet opgerolde deel
van elk van de kabels 13.5m. Hoe hoog hangt de onderkant van het bord dan boven de fundering?
(A) H = 3.5m
(B) H = 4m
Oplossing: D
juist beantwoord: 76 %
blanco: 17 %
(C) H = 4.5m
(D) H = 5m
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 10
Oefening 14
Beschouw de volgende uitspraak.
“Alle deelnemers aan de ijkingstoets zijn hip.”
Welke uitspraak is hiermee equivalent?
(A) Wie niet hip is, neemt niet deel aan de ijkingstoets.
(B) Wie niet deelneemt aan de ijkingstoets, is niet hip.
(C) Wie hip is, neemt deel aan de ijkingstoets.
(D) Er bestaan mensen die niet deelnemen aan de ijkingstoets en niet hip zijn.
Oplossing: A
juist beantwoord: 48 %
blanco: 10 %
Oefening 15
−2x3 + x2 + 2
A
B
Cx + D
kan men schrijven als volgt:
+ 2+ 2
.
x2 (x2 + 2)
x
x
x +2
Waaraan is A + B + C + D gelijk?
De breuk
(A) −1
(B) −2
(C) −4
(D) −5
Oplossing: A
juist beantwoord: 57 %
blanco: 33 %
Oefening 16
Beschouw de functie f : R → R met onderstaande grafiek.
f (x)
2
-1
0
x
1
-2
Verder zijn de volgende functies gegeven:
g : R → R : x 7→ g(x) = sin x
h : R → R : x 7→ h(x) = f (g(x))
Bepaal de afgeleide h0 (5π/3).
(A) 0
(B) 1
Oplossing: B
juist beantwoord: 45 %
blanco: 20 %
(C) 2
(D) 10π/3
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 11
Oefening 17
Bij een trillende snaar kan de uitwijking D op een positie x en tijdstip t beschreven worden als
2πt
2πx
D = A sin(
) cos(
), waarbij λ > 0 de golflengte, T > 0 de periode, en A > 0 de amplitude van de golf is.
λ
T
Welk van onderstaande grafieken toont het verband tussen de uitwijking D en de positie x op tijdstip t = T /2?
(A)
(B)
A
A
0
λ
x
(C)
0
λ
x
0
λ
x
(D)
A
A
0
λ
x
Oplossing: D
juist beantwoord: 54 %
blanco: 20 %
Oefening 18
Welke van onderstaande beweringen is geldig voor elk reëel getal x < −1?
p
(A)
(x + 1)2 > −x − 1
p
√
(B)
(x + 1)2 > x2 + 1
√
p
(x + 1)2 < x2 + 1
(C)
p
(D) (x + 1)2 < x
Oplossing: C
juist beantwoord: 84 %
blanco: 3 %
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 12
Oefening 19
Bepaal de oppervlakte van de driehoek BCD in onderstaande figuur.
D
√
6
(A)
30◦
A
Oplossing: D
juist beantwoord: 73 %
blanco: 23 %
C
3
(B)
7
4
(C)
√3
2
(D)
√
3+ 3
2
B
1
√
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 13
Oefening 20
Toelichting doorsnedes
Bij doorsnedes wordt gebruik gemaakt van enkele tekenconventies die kort worden toegelicht. Bij de ruimtelijke
voorstelling wordt een doorzichtig snijvlak aangegeven en een kijkrichting. Dit laatste op twee manieren:
• De letters ’AB’ bevinden zich in het snijvlak en zijn vanuit het standpunt van de waarnemer normaal leesbaar.
• De streepjes aan de hoeken van het vlak bevinden zich achter het snijvlak vanuit de waarnemer gezien.
Bij de voorstelling van de snede gelden volgende afspraken:
• Delen van het object die gesneden worden hebben een dikke rand en zijn grijs ingekleurd
• Delen waarop men kijkt hebben een dunne rand en zijn niet ingekleurd
• Delen voor het snijvlak (ten opzichte van de waarnemer) hebben een streepjeslijn als grens en zijn niet ingekleurd
Een dikke lijn heeft voorrang op een dunne, die op zijn beurt voorrang heeft op een streepjeslijn. Een grijze inkleuring
heeft voorrang op een streepjeslijn.
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 14
Hieronder een snede van een object.
De positie van de letters ’AB’ in de snedetekening heeft enkel tot doel om de kijkrichting aan te geven en heeft geen
verband met de positie van de letters in de isometrie.
Geef de letter van het object met aanduiding van het snedevlak dat hiermee overeenkomt.
Oplossing: D
juist beantwoord: 91 %
blanco: 6 %
(A)
(B)
(C)
(D)
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 15
Oefening 21
Drie metalen cilinders met straal R worden gemonteerd zodat ze onderling raken. Nadien worden ze aan een centrale
staaf met straal r bevestigd. Deze centrale staaf raakt de drie cilinders. De verhouding Rr is een getal dat aan één van
onderstaande ongelijkheden voldoet. Welke?
(A) 0, 05 <
(B) 0, 1 <
r
R
(C) 0, 15 <
(D) 0, 2 <
r
R
≤ 0, 15
r
R
r
R
≤ 0, 1
≤ 0, 2
≤ 0, 25
Oplossing: C
juist beantwoord: 11 %
blanco: 71 %
Oefening 22
Een functie f : R → R noemen we even als f (−x) = f (x) voor alle x ∈ R.
Een functie f : R → R noemen we oneven als f (−x) = −f (x) voor alle x ∈ R.
Precies één van onderstaande beweringen is fout. Welke?
(A) Als f een oneven functie is en g een even functie, dan is de functie h : R → R gegeven door
h(x) = f (x) g(x) oneven.
(B) Als f een oneven functie is, dan is de functie h : R → R gegeven door h(x) = (f (x))2 even.
(C) Als f een oneven functie is, dan is de functie h : R → R gegeven door h(x) = f (x + x3 ) oneven.
(D) Als f een oneven functie is, dan is de functie h : R → R gegeven door h(x) = −f (x2 ) oneven.
Oplossing: D
juist beantwoord: 63 %
blanco: 14 %
Oefening 23
Mia fietst dagelijks naar haar werk. Met haar stadsfiets duurt de fietstocht 40 minuten. Op de rechte stukken rijdt ze
met een gemiddelde snelheid van 20 km/u. De overige 2 km rijdt ze met een gemiddelde snelheid van 12 km/u.
Met een elektrische fiets is haar gemiddelde snelheid 20% hoger op de rechte stukken. De overige 2 km rijdt ze nog
steeds met een gemiddelde snelheid van 12 km/u. Hoe lang doet Mia over de tocht wanneer ze de elektrische fiets
gebruikt?
(A) 33 minuten
Oplossing: C
juist beantwoord: 85 %
blanco: 5 %
(B) 34 minuten
(C) 35 minuten
(D) 36 minuten
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 16
Oefening 24
Cedric is de 4-cijferige code van zijn GSM vergeten, maar herinnert zich wel het volgende :
• De code bevat geen enkel cijfer 0, 6, 7, 8 of 9.
• De code bevat slechts 3 verschillende cijfers (1 cijfer komt dus 2 keer voor).
• De cijfers in de code zijn van klein naar groot geordend.
Noemen we N het aantal verschillende codes die Cedric moet testen om zijn GSM zeker te kunnen ontgrendelen. In
welk interval ligt N ?
(A) 0 < N ≤ 10
(B) 10 < N ≤ 20
(C) 20 < N ≤ 30
(D) N > 30
Oplossing: C
juist beantwoord: 45 %
blanco: 16 %
Oefening 25
Gegeven de functie f : R → R met als grafiek een rechte door de punten (0, 1) en (3, 7).
Z 3
Bepaal
2f (x2 ) + 1 dx
0
(A) 12
(B) 21
(C) 45
(D) 153
Oplossing: C
juist beantwoord: 73 %
blanco: 17 %
Oefening 26
r
Voor welk van onderstaande waarden voor x ∈ R is de uitdrukking
(A) -1
(B) -3/4
Oplossing: B
juist beantwoord: 46 %
blanco: 20 %
(C) -1/3
ln (−2x2 − x + 1)
gedefinieerd?
−4x2 − x
(D) -1/4
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 17
Oefening 27
Een circusartiest zit op een schommel die heen en weer wiegt. De touwen van de schommel hebben een lengte l = 4 m.
Het verband tussen de tijd t uitgedrukt
in seconden (s) en de hoek θ die het touw maakt met de verticale wordt
!
r
π
10
gegeven door θ = cos
t , met l de lengte van het touw in meter. Hoeveel keer passeert de schommel door de
6
l
√
verticale stand in het tijdsinterval [0, 10]?
(A) 1 keer
(B) 2 keer
(C) 3 keer
(D) 4 keer
Oplossing: B
juist beantwoord: 22 %
blanco: 54 %
Oefening 28
Bij een bepaalde populatie is griep de meest voorkomende ziekte. De kans dat iemand uit deze populatie griep heeft is
1%. Mensen met griep hebben 54.5% kans om koorts te hebben. Mensen zonder griep (maar met mogelijk een andere
ziekte) hebben 4.5% kans om koorts te hebben. Beschouw een willekeurige persoon uit de populatie. De persoon heeft
koorts. Wat is de kans dat de persoon griep heeft?
(A) 1%
(B) 10.9%
(C) 45.5%
(D) 54.5%
Oplossing: B
juist beantwoord: 56 %
blanco: 25 %
Oefening 29
De vier reële getallen a, b, c en d zijn zo gekozen dat er geldt
1 a a 1
c
d
=
1 b b 1
−d −c
Hoeveel verschillende waarden kan de grootheid a + b aannemen ?
(A) 0
(B) 1
Oplossing: C
juist beantwoord: 28 %
blanco: 44 %
(C) 2
(D) meer dan 2
IJkingstoets burgerlijk ingenieur 12 september 2016 - reeks 1 - p. 18
Oefening 30
Doorheen een weerstand loopt een stroom i(t) waarvan het verloop getoond wordt in onderstaande figuur. Het
Z
1 T 2
gemiddeld vermogen kan berekend worden als
Ri (t) dt, met R een reële constante. Bereken het gemiddeld
T 0
vermogen.
i(t)
I0
0
T
4
T
2
3T
4
T
5T
4
t
3T
2
−I0
(A) 2RI02
Oplossing: C
juist beantwoord: 16 %
blanco: 74 %
(B) RI02
(C)
RI02
3
(D)
2RI02
T