Junior Wiskunde Olympiade 2016-2017: tweede ronde

Junior Wiskunde Olympiade 2016-2017: tweede ronde
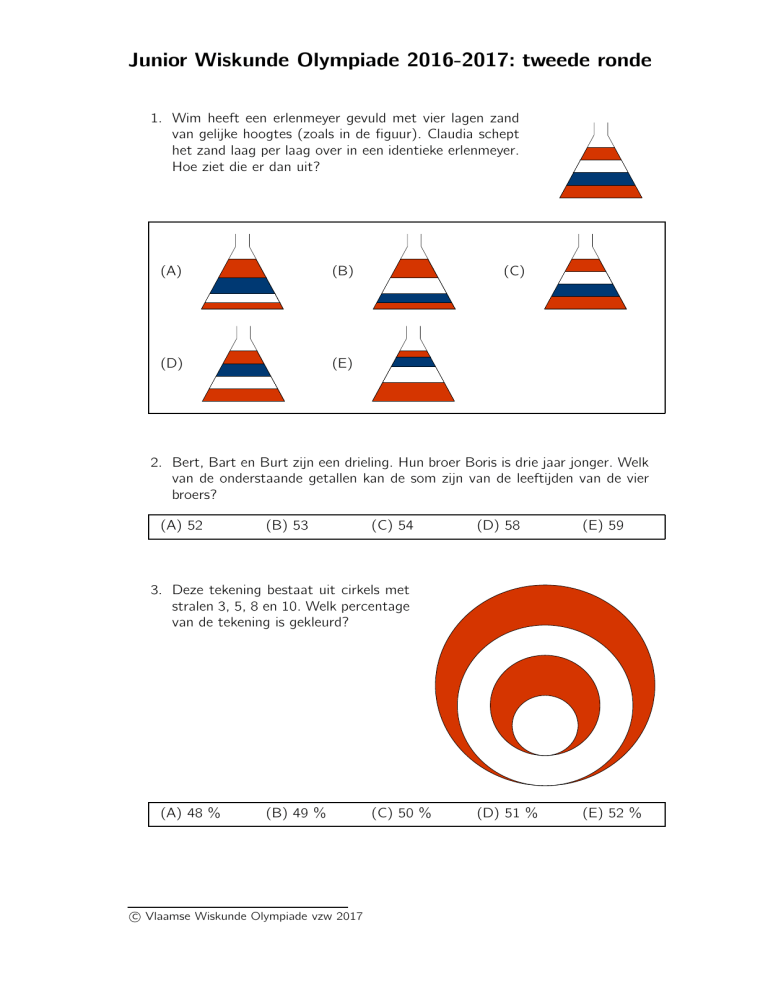
1. Wim heeft een erlenmeyer gevuld met vier lagen zand
van gelijke hoogtes (zoals in de figuur). Claudia schept
het zand laag per laag over in een identieke erlenmeyer.
Hoe ziet die er dan uit?
(A)
(B)
(D)
(E)
(C)
2. Bert, Bart en Burt zijn een drieling. Hun broer Boris is drie jaar jonger. Welk
van de onderstaande getallen kan de som zijn van de leeftijden van de vier
broers?
(A) 52
(B) 53
(C) 54
(D) 58
(E) 59
(D) 51 %
(E) 52 %
3. Deze tekening bestaat uit cirkels met
stralen 3, 5, 8 en 10. Welk percentage
van de tekening is gekleurd?
(A) 48 %
(B) 49 %
c Vlaamse Wiskunde Olympiade vzw 2017
(C) 50 %
4. Jef heeft een stappenteller, maar kan door een technische fout de laatste
twee cijfers niet zien. Als de stappenteller bijvoorbeeld 1245 stappen meet,
zal Jef 12 op het schermpje zien. Aan het begin van een wandeling leest
Jef 23 op zijn teller. Na de wandeling ziet hij 35 . Hoeveel stappen heeft
Jef tijdens de wandeling met zekerheid minstens gezet?
(A) 1100
(B) 1101
(C) 1102
(D) 1200
(E) 1299
(D) 5π en 6π
(E) 6π en 7π
5. Zeven cirkels met straal 1 raken elkaar
zoals op de figuur. Door zes van de zeven
middelpunten te verbinden, ontstaat een
regelmatige zeshoek. De oppervlakte van
deze zeshoek ligt dan tussen
(A) 2π en 3π
(B) 3π en 4π
(C) 4π en 5π
6. Bernd leest wiskundige uitdrukkingen van rechts naar links. Bijvoorbeeld:
(X + Y ) − M leest hij als M −(Y +X). Lisa leest ze op de gewone manier. Bij
welke van de volgende uitdrukkingen krijgen Bernd en Lisa een verschillend
resultaat?
(A) (X + Y )(X + Y )
(B) (8X + Y ) · X
(C) (X + Y )(X − Y )
(D) (X − Y )(X − Y )
(E) (X − Y ) − (X − Y )
7. De diagonaal [BD] van het vierkant ABCD
met zijde 6 wordt verlengd tot P zodanig dat
|P D| = 4|BD|. Hoe groot is de oppervlakte
van △P BC?
(A) 24
(B) 36
(C) 48
P
A
B
D
C
(D) 54
(E) 72
√ √
√
8. Een driehoek heeft zijden 2, 5 en 7 en grootste hoek α. Welke van de
volgende beweringen is dan correct?
(A) α 6 70◦
(B) 70◦ < α 6 90◦
(C) 90◦ < α 6 110◦
(D) α > 110◦
(E) Zo’n driehoek bestaat niet.
9. De Chinese keizers uit de Ming-dynastie brachten offers op een plein dat
gemaakt is van grote witte stenen (zie figuur). Het aantal stenen in de
verschillende ringen zijn opeenvolgende negenvouden. Hoeveel witte stenen
bevinden zich op dit plein?
(A) 405
(B) 450
(C) 504
(D) 540
(E) 544
10. Welk van de volgende getallen is geen deler van 322017 + 322018 ?
(A) 22
(B) 33
(C) 44
(D) 55
(E) 66
11. Bart en Stijn trekken aan de uiteinden van een touw met zes knopen A, B, C,
D, E en F . Er liggen juist drie knopen tussen knoop B en knoop C. Knoop
D ligt dichter bij Stijn dan knoop B en dichter bij Bart dan knoop F . Naast
F ligt maar één knoop. Welke?
Bart
(A) A
(B) B
•
•
•
(C) C
•
• •
Stijn
(D) D
(E) E
12. Een schatrijke oom laat aan zijn vier nichtjes zijn fortuin na. Een derde van
zijn fortuin gaat naar An. Een derde van wat dan nog overblijft gaat naar
Bieke. Een derde van wat dan nog overblijft gaat naar Charlotte en wat
daarna nog overblijft gaat naar Dina. Wat is de verhouding van het deel van
Charlotte tot het deel van Dina?
(A)
1
2
(B)
2
3
(C)
11
9
(D)
3
2
(E)
2
1
13. In een klas zitten 50 % meer jongens dan meisjes. Van de jongens is 62 %
geslaagd en van de hele klas is 68 % geslaagd. Hoeveel procent van de meisjes
is geslaagd?
(A) 68 %
(B) 71 %
(C) 74 %
(D) 77 %
(E) 80 %
14. De politie ondervraagt vijf leden van een Chinese dievenbende: Pang, Peng,
Ping, Pong en Pung. Eén van hen pleegde een diefstal. Om elkaar te
beschermen spreken de dieven af dat precies één van hen zal liegen.
• Pang zegt: “Peng heeft het niet gedaan.”
• Peng zegt: “Ping heeft het niet gedaan.”
• Ping zegt: “Pong liegt.”
• Pong zegt: “Ik heb het gedaan.”
• Pung zegt: “Het was Pang of Peng.”
Wie heeft de diefstal gepleegd?
(A) Pang
(B) Peng
(C) Ping
(D) Pong
(E) Pung
<
<
15. In onderstaande futoshiki moet in elk vakje het getal 1, 2, 3, 4 of 5 geplaatst
worden, zodat op elke rij en op elke kolom ieder getal juist één keer voorkomt.
De aangegeven ongelijkheden moeten kloppen.
<
<
<
<
<
<
3
>
Welk getal hoort in het gekleurde vakje?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
16. Wat is de grootst mogelijke waarde van x y indien x en y verschillende getallen
zijn uit de verzameling {−2, −3, −4, −5} ?
(A)
1
25
(B)
1
9
(C)
1
8
(D) 625
(E) 1024
17. Mathias en Hanne fietsen aanvankelijk op 2 km afstand van elkaar. Op elk
punt van de onderstaande route rijden ze even snel: 10 km/h bergop, 60
km/h bergaf en 40 km/h elders. Hoe ver rijden ze van elkaar op het moment
dat Hanne het ijssalon passeert?
5 km
10 km
7 km
®
®
•
•
Mathias Hanne
(A) 2,5 km
(B) 3 km
•
ijssalon
(C) 3,5 km
(D) 4 km
(E) 4,5 km
18. Op een lange tak zitten 51 kraaien naast elkaar. Als een kraai krast, vliegen
zijn linkerbuur en zijn rechterbuur weg (indien deze buren bestaan). Een kraai
die wegvliegt, komt na precies 1 minuut weer terug naar dezelfde plaats op
de tak en krast onmiddellijk. De uiterst linkse kraai krast als eerste. Hoe vaak
zal de uiterst rechtse kraai wegvliegen in een tijdspanne van 1 uur?
(A) 6
(B) 7
(C) 9
(D) 11
(E) 26
19. Een tank heeft een rupsband die draait rond vijf wielen. De wielen hebben
een diameter van 20 cm en een tussenafstand van 20 cm. Hoeveel meter rijdt
de tank bij één omwenteling van de rupsband?
8+π
meter
5
20 + π
(D)
meter
5
(A)
16 + π
meter
5
20 + 2π
(E)
meter
5
(B)
(C)
18 + π
meter
5
20. Een trapezium met kleine basis 2 en grote basis 5 wordt door zijn diagonalen
in vier driehoeken verdeeld. De driehoek aan de kleine basis heeft oppervlakte
4. Wat is de oppervlakte van dit trapezium?
(A) 32
(B) 40
(C) 45
(D) 49
(E) 50
21. In de rij getallen a, 20, b, c, d, e, f , g, 17 is de som van elke vier
opeenvolgende termen gelijk aan 50. Hoeveel is b + g?
(A) 13
(B) 14
(C) 15
(D) 16
(E) 17
22. De convexe vierhoek ABCD heeft minstens drie gelijke zijden en minstens
twee gelijke hoeken. Wat is de kleinste van de volgende verzamelingen waartoe
vierhoek ABCD zeker behoort?
(A) De vierkanten
(B) De ruiten
(D) De trapezia
(E) De vierhoeken
(C) De parallellogrammen
23. Billy wil aan Joël een inlogcode van zes cijfers mailen, maar vergeet één van
de cijfers. Joël ontvangt de code 42972. Hoeveel keer moet Joël een code
proberen om zeker in te loggen?
(A) 50
(B) 54
(C) 55
(D) 56
(E) 60
24. Bepaal α + β.
α
β
(A) 20◦
(B) 22,5◦
(C) 25◦
(D) 27,5◦
(E) 30◦
25. In een kluis bewaart Sofia 26 biljetten: een aantal van 100 euro, 200 euro en
500 euro. Als ze 20 biljetten neemt, zal ze minstens 1 biljet van 100 euro
hebben, minstens 2 biljetten van 200 euro en minstens 5 biljetten van 500
euro. Wat is het totale bedrag van de biljetten die in de kluis liggen?
(A) 4500 euro
(B) 5600 euro
(C) 6700 euro
26. In driehoek △ABC verbindt men A en Q
met P zodat drie gelijke hoeken ontstaan
zoals in de figuur. Als |AP | = |BP | = 14
en |P C| = 21, wat is dan de lengte van
[P Q]?
(A) 7
(B) 8
(C) 8,4
(D) 7800 euro (E) 8900 euro
A
Q
B
C
P
(D) 8,5
(E) 9
27. Als x 2 = x + 1 en x 7 = 13x + y , waaraan is y dan gelijk?
(A) 3
(B) 5
(C) 8
(D) 13
(E) 21
28. Pieter kent een geheim.
• Hij vertelt het aan vier jongens waaronder Arne.
• Arne vertelt het geheim verder aan vijf jongens waaronder Robin.
• Robin vertelt het geheim op zijn beurt aan drie jongens waaronder Evan.
• Evan tot slot vertelt het geheim aan zes jongens.
De jongens vertellen het geheim uiteraard niet aan de persoon van wie ze
het gehoord hebben. Pieter, Arne, Robin en Evan vertellen het geheim niet
aan meer dan één jongen tegelijkertijd. Geen enkele jongen weet dus welke
andere jongen het geheim al kent. Wat is het minimum aantal jongens dat
het geheim kent?
(A) 7
(B) 8
(C) 14
(D) 19
(E) 20
29. De cijfers 1, 2, 3, 4, 5, 6, 7, 8 en 9 worden in deze volgorde vervangen door
opeenvolgende letters van het alfabet. Als je weet dat uspmru het kwadraat
van een natuurlijk getal is, wat is dan dat natuurlijk getal?
(A) pmr
(B) uts
(C) qop
(D) upm
30. De lijnstukken [P Q], [P R] en [AR] verdelen
driehoek △ABC in vier driehoeken met
dezelfde oppervlakte, zoals in de figuur. Hoe
verhouden de lengten van de lijnstukken
[BQ], [QR] en [RC] zich?
A
P
B
(A) 1 : 1 : 1
(B) 2 : 2 : 1
(C) 3 : 3 : 1
(E) rrn
Q
(D) 3 : 2 : 1
R
C
(E) 3 : 3 : 2