Appendix: Zwaartepunten

Appendix: Zwaartepunten
Enkele opmerkingen vooraf:
• Maak altijd eerst een schets van het betreffende gebied (en dat hoeft heus niet zo precies te zijn
als de grafieken die ik hier door de computer kan laten tekenen).
• Ik schrijf sin x zonder haakjes omdat het mag, maar sin(2x) mèt haakjes omdat het moet. Anders
(bij de notatie sin 2x zonder haakjes) zou je kunnen denken dat er sin(2) · x bedoeld wordt. Bij
sin x bestaat die verwarring niet: dat kan alleen maar sin(x) betekenen, dus mag je zelf kiezen of
je de haakjes wel of niet opschrijft.
• Ik schrijf [f (x)]2 i.p.v. f 2 (x) om verwarring te voorkomen. Bij de notatie f 2 (x) zou je nl. ook
kunnen denken dat er f (f (x)) bedoeld wordt (dus: x invullen in f en dat resultaat weer opnieuw
invullen in f ). [f (x)]2 betekent: x invullen in f en dat resultaat kwadrateren). Wel gebruik ik de
notatie sin2 (x) = (sin x)2 omdat haast iedereen dat doet.
• Ik bereken niet direct de coördinaten x en y van het zwaartepunt, maar bereken eerst als tussenstap
Ax (dit wordt ook wel het totale moment t.o.v. de y-as genoemd) en 2Ay (dit is gelijk aan twee
1
op hoeft
keer het totale moment Ay t.o.v. de x-as). Doordat je zo niet steeds de breuken A1 en 2A
te schrijven, maak je minder snel rekenfouten bij het uitwerken van de integralen.
• Denk erom dat je soms één of beide coördinaten van het zwaartepunt al direct kunt aflezen uit de
grafiek, nl. als het gebied symmetrisch is. Dit kan veel rekenwerk schelen. Omschrijf dit inzicht
altijd wel in woorden, anders weet iemand anders (die je werk nakijkt) niet hoe je op je antwoord
bent gekomen.
door Jan-Jaap Oosterwijk
Opgaven
Bepaal van elk van de volgende gebieden de coördinaten van het zwaartepunt.
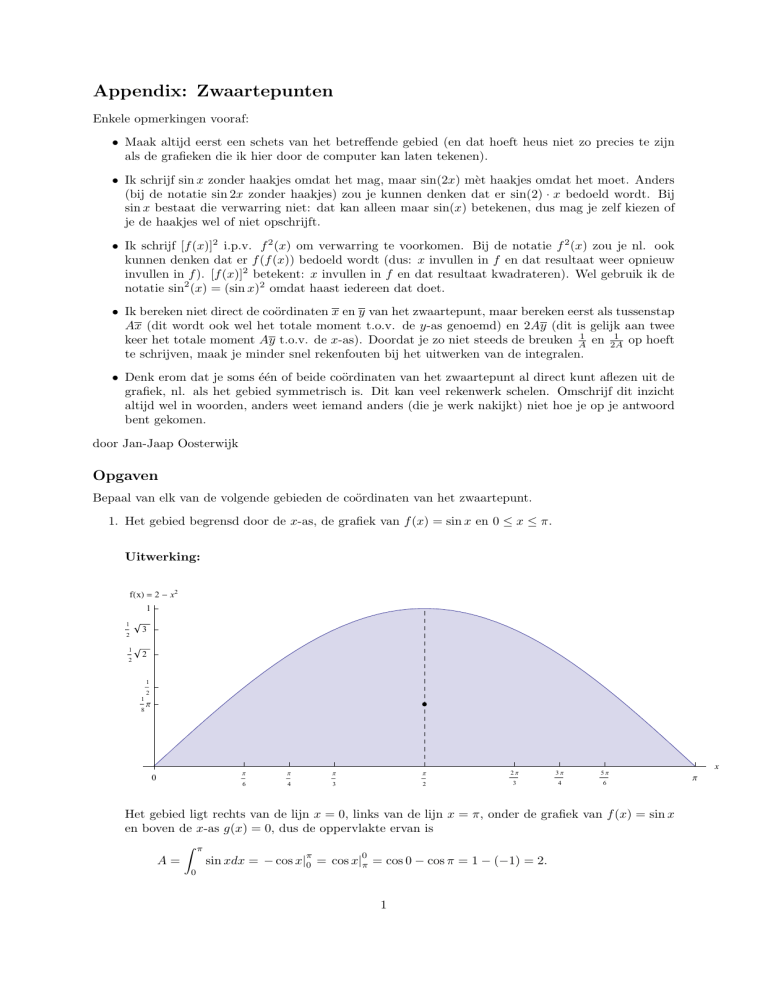
1. Het gebied begrensd door de x-as, de grafiek van f (x) = sin x en 0 ≤ x ≤ π.
Uitwerking:
fHxL = 2 - x2
1
1
2
1
2
3
2
1
2
1
8
Π
0
Π
Π
Π
Π
2Π
3Π
5Π
6
4
3
2
3
4
6
Het gebied ligt rechts van de lijn x = 0, links van de lijn x = π, onder de grafiek van f (x) = sin x
en boven de x-as g(x) = 0, dus de oppervlakte ervan is
Z π
π
0
A=
sin xdx = − cos x|0 = cos x|π = cos 0 − cos π = 1 − (−1) = 2.
0
1
x
Π
Het totale moment t.o.v. de y-as is
Z π
Z π
π
x sin xdx = −x cos x|0 −
− cos xdx
Ax =
0
0
Z π
π
π
π
cos xdx = −x cos x|0 + sin x|0 = (π − 0) + (0 − 0) = π
= −x cos x|0 +
0
(je gebruikt hier partiële integratie), dus het x-coördinaat van het zwaartepunt is x = A1 π = 12 π.
Op zich had je dit ook al direct kunnen aflezen uit de grafiek, want het gebied is spiegelsymmetrisch
t.o.v. de lijn x = 12 π. Het zwaartepunt ligt altijd op een symmetrie-as, als die er is.
Twee keer het totale moment t.o.v. de x-as is
Z π
Z π
1
1
1
sin2 xdx =
2Ay =
2 − 2 cos(2x) dx = 2 x −
0
0
1
4
π
sin(2x) 0 = 21 π
(je gebruikt hier de verdubbelingsformule cos(2x) = 1 − 2 sin2 x in omgekeerde vorm: deze truc
is besproken in de laatste week van Calculus 1 en staat in het boek beschreven in §6.3), dus het
1
· 12 π = 18 π. Het zwaartepunt van het gebied is dus
y-coördinaat van het zwaartepunt is y = 2A
1
1
( 2 π, 8 π).
NB:
Je had de spiegelsymmetrie ook al kunnen gebruiken bij het berekenen van de oppervlakte A, door
op te merken dat de oppervlakte van het totale gebied gelijk is aan twee keer de oppervlakte van
het gebied aan slechts één kant van de symmetrie-as, oftewel
Z
A=2
0
1
2π
sin xdx = . . . = 2(cos 0 − cos( 12 π)) = 2(1 − 0) = 2.
In deze opgave maakt het weinig uit welke van de twee methodes je gebruikt: ze kosten beiden
evenveel moeite (maar vaak kan zulk meetkundig inzicht erg veel werk schelen: dit wordt duidelijk
in de volgende opgaven).
2. Het gebied dat gegeven wordt door 0 ≤ y ≤ 2 − x2 .
Uitwerking:
fHxL = 2 - x2
2
1
4
5
x
- 2
-1
1
2
2
Het gebied ligt onder de grafiek van f (x) = 2 − x2 en boven√de x-as g(x) =
√0. De grafiek van f (x)
snijdt de x-as daar waar 2 − x2 = 0. Dat gebeurt bij x = − 2 en bij x = 2. De oppervlakte van
het gebied is dus
√
√
√
√
√
√
2
2
2
(2 − x2 )dx = [2x − 13 x3 ]−√
=
(2
2
−
2)
−
(−2
2
+
2)
3
3
2
− 2
√
√
√
√
= 2(2 2 − 23 2) = 2 · 43 2 = 38 2.
Z
A=
2
√
Je ziet dat je hier eigenlijk twee keer hetzelfde berekent. Dit wijst erop dat er al direct een
makkelijkere methode was: merk nl. op dat het gebied spiegelsymmetrisch is t.o.v. de y-as x = 0.
Je had de oppervlakte dus ook als volgt kunnen berekenen:
√
Z
2
A=2
0
√
√
√
√
(2 − x2 )dx = 2[2x − 13 x3 ]0 2 = 2(2 2 − 23 2) = . . . = 83 2.
Het totale moment t.o.v. de y-as is
√
Z
Ax =
√
2
2
√
− 2
x(2 − x )dx =
Z
2
√
− 2
√
2
(2x − x3 )dx = [x2 − 41 x4 ]−√
= 1 − 1 = 0.
2
Je had ook kunnen herkennen dat
√
Z
Ax =
2
√
√
− 2
2
x(2 − x2 )dx = [− 14 (2 − x2 )2 ]−√
=0−0=0
2
(het integreren doe je hier via een substitutie, alhoewel ik de details ervan niet heb opgeschreven).
Het x-coördinaat van het zwaartepunt is dus x = 0. Je had dit ook al direct kunnen aflezen uit de
grafiek, want het gebied is spiegelsymmetrisch t.o.v. de y-as x = 0.
Twee keer het totale moment t.o.v. de x-as is
√
Z
√
2
Z
2
√
2
2
4
4 3
1 5 √
√ (2 − x ) dx =
√ (4 − 4x + x )dx = [4x − 3 x + 5 x ]− 2
− 2
− 2
√
√
= . . . = 2(4 − 83 + 45 ) 2 = 64
15 2
2 2
2Ay =
dus het y-coördinaat van het zwaartepunt is y =
is dus (0, 45 ).
1
2A
·
64
15
√
2 = 45 . Het zwaartepunt van het gebied
3. Het gebied dat begrensd wordt door de x-as, de grafiek van f (x) =
√
R2 − x2 en −R ≤ x ≤ R.
Uitwerking:
R2 - x2
fHxL =
R
4R
3Π
-R
R
3
x
R wordt een parameter genoemd: een willekeurige constante. In dit geval mag R elke√positieve
waarde aannemen die je maar kunt bedenken. Het gebied ligt onder de grafiek van f (x) = R2 − x2
(een halve cirkel (met positieve y-coördinaat) van een cirkel met straal R en met de oorsprong als
middelpunt) en boven de x-as g(x) = 0. De cirkelboog snijdt de x-as bij x = −R en bij x = R. De
oppervlakte van het gebied is dus
Z
R
p
A=
R2 − x2 dx = 2
Z
−R
R
p
R2 − x2 dx.
0
(we hebben het hier ons alvast iets makkelijker gemaakt door de spiegelsymmetrie rond de y-as
x = 0 te gebruiken). Als je deze integraal wil uitrekenen zit er helaas niets anders op (dat is
niet helemaal waar; als je dit te moeilijk vindt om te volgen, sla dit stuk dan eerst over en kijk
alvast naar de volgende alinea) dan de goniometrische substitutie x = R sin θ te gebruiken waarbij
0 ≤ θ ≤ 21 π (ook deze truc is besproken in de laatste week van Calculus 1 en staat in het boek
beschreven in §6.3.) De grenzen x = 0 en x = R komen overeen met θ = 0 en θ = 21 π. De integrand
wordt
q
p
p
√
R2 − x2 = R2 − R2 sin2 θ = R2 (1 − sin2 θ) = R2 cos2 θ = R| cos θ|
en op het interval 0 ≤ θ ≤ 12 π is | cos θ| = cos θ. Verder is
R
Z
p
A=2
R2
−
x2 dx
Z
=2
1
2π
dx
dθ
= R cos θ, dus dx = R cos θdθ, dus
R cos θ · R cos θdθ = 2R
2
0
0
Z
1
2π
cos2 θdθ.
0
Gebruik hier weer een omgekeerde verdubbelingsformule en vind tenslotte dat
A = 2R
2
1
2π
Z
0
( 12
+
1
2
cos(2θ))dθ = R
2
Z
1
2π
1
(1 + cos(2θ))dθ = R2 [θ +
0
1
2
π
sin(2θ)]02 = 12 πR2 .
(Lees hier verder ) Deze opgave is een goed voorbeeld van hoe meetkundig inzicht je soms een hoop
werk kan besparen. Er is nl. gelukkig ook een makkelijkere manier om A te bepalen. In plaats
van deze ingewikkelde berekening had je ook direct kunnen opschrijven dat A de helft is van de
oppervlakte van een cirkel met straal R, waar je de formule al voor uit je hoofd kent. Zo had je
direct ingezien dat inderdaad A = 21 πR2 .
Het totale moment t.o.v. de y-as is
Z
R
Ax =
x
−R
p
R
p
R2 − x2 dx = − R2 − x2 = 0 − 0 = 0.
−R
(het integreren doe je hier via een substitutie, alhoewel ik de details ervan niet heb opgeschreven).
Dit had je ook af kunnen lezen uit de grafiek, want het gebied is spiegelsymmetrisch t.o.v. de y-as
x = 0. Twee keer het totale moment t.o.v. de x-as is
Z R p
Z R
Z R
( R2 − x2 )2 dx =
(R2 − x2 )dx = 2
(R2 − x2 )dx
2Ay =
−R
−R
0
3
1 3
4 3
= 2[R2 x − 31 x3 ]R
0 = 2(R − 3 R ) = 3 R .
Dit lijkt trouwens erg op de berekening van de oppervlakte in de vorige opgave, waar R = 2. Dus
1
· 43 R3 = 4R
het y-coördinaat van het zwaartepunt is y = 2A
3π . Het zwaartepunt van de halve cirkel
4R
is dus (0, 3π ).
√
4. Het gebied dat begrensd wordt door de grafieken van f (x) = x en g(x) = x2 , waarbij 0 ≤ x ≤ 1.
4
Uitwerking:
y
1
9
20
x
9
0
1
20
Het gebied ligt rechts van de lijn x = 0, links van de lijn x = 1, onder de grafiek van f (x) =
boven de grafiek van g(x) = x2 , dus de oppervlakte ervan is
Z
A=
0
1
√
x en
√
√
( x − x2 )dx = [ 23 x x − 13 x3 ]10 = 31 .
Het totale moment t.o.v. de y-as is
Z 1
Z 1
√
√
√
2
Ax =
x( x − x )dx =
(x x − x3 )dx = [ 52 x2 x − 41 x4 ]10 =
0
0
dus het x-coördinaat van het zwaartepunt is x =
1
A
·
3
20
=
0
dus het y-coördinaat van het zwaartepunt is y =
9
9
, 20
).
dus ( 20
1
2A
·
3
10
=
−
1
4
=
3
20 ,
9
20 .
Twee keer het totale moment t.o.v. de x-as is
Z 1
Z 1
√ 2
2 2
2Ay =
( x) − (x ) dx =
(x − x4 )dx = [ 21 x2 − 15 x5 ]10 =
0
2
5
9
20 .
1
2
−
1
5
=
3
10 ,
Het zwaartepunt van het gebied is
Merk op dat in deze opgave x = y. Op zich had je dit ook al direct kunnen aflezen uit de grafiek
(en dus slechts één van de twee coördinaten van het zwaartepunt hoeven te berekenen), want het
gebied is spiegelsymmetrisch t.o.v. de lijn y = x. Het zwaartepunt ligt altijd op een symmetrie-as,
als die er is.
NB:
Je had de spiegelsymmetrie ook al kunnen gebruiken bij het berekenen van de oppervlakte A, door
op te merken dat de oppervlakte van het totale gebied gelijk is aan twee keer de oppervlakte van
het gebied aan slechts één kant van de symmetrie-as, oftewel
Z 1
A=2
(x − x2 )dx = 2[ 12 x2 − 13 x3 ]10 = 2( 12 − 13 ) = 13 .
0
5