FORMULES, OUDE EN NIEUWE 1 Het weer hogerop Hoog in de

FORMULES, OUDE EN NIEUWE
1
Het weer hogerop
Hoog in de bergen is de lucht kouder en ijler dan beneden in het dal: de temperatuur en de luchtdruk zijn
daar lager.
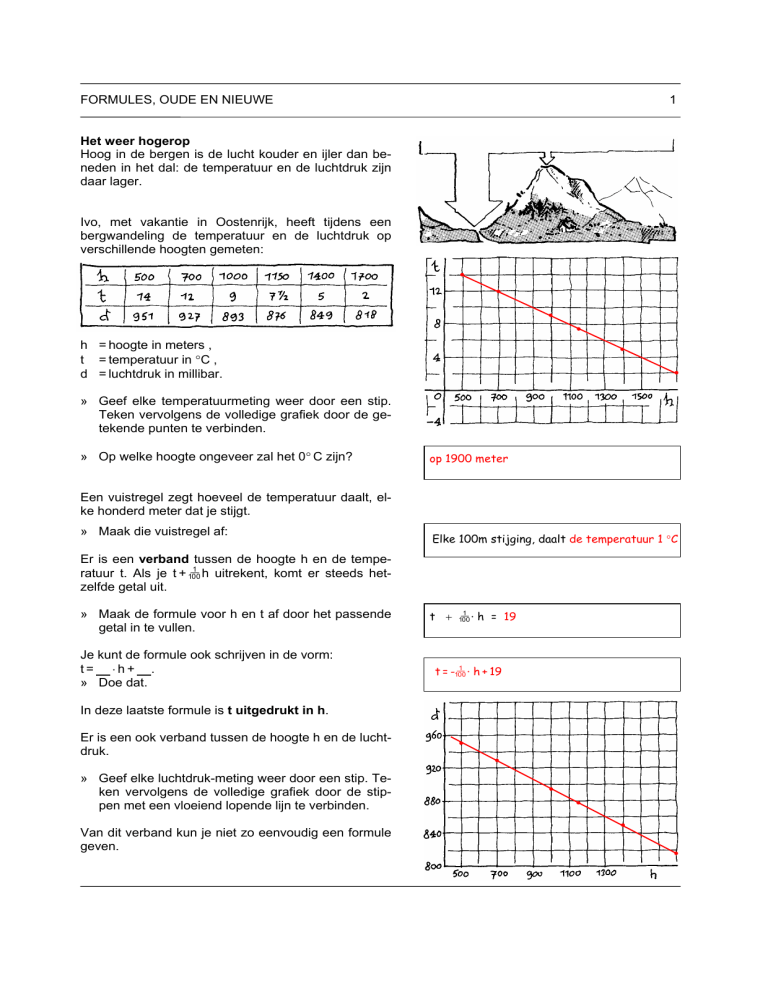
Ivo, met vakantie in Oostenrijk, heeft tijdens een
bergwandeling de temperatuur en de luchtdruk op
verschillende hoogten gemeten:
h = hoogte in meters ,
t = temperatuur in °C ,
d = luchtdruk in millibar.
» Geef elke temperatuurmeting weer door een stip.
Teken vervolgens de volledige grafiek door de getekende punten te verbinden.
» Op welke hoogte ongeveer zal het 0° C zijn?
op 1900 meter
Een vuistregel zegt hoeveel de temperatuur daalt, elke honderd meter dat je stijgt.
» Maak die vuistregel af:
Elke 100m stijging, daalt de temperatuur 1 °C
Er is een verband tussen de hoogte h en de temperatuur t. Als je t + @h uitrekent, komt er steeds hetzelfde getal uit.
» Maak de formule voor h en t af door het passende
getal in te vullen.
Je kunt de formule ook schrijven in de vorm:
t = ⋅ h + .
» Doe dat.
In deze laatste formule is t uitgedrukt in h.
Er is een ook verband tussen de hoogte h en de luchtdruk.
» Geef elke luchtdruk-meting weer door een stip. Teken vervolgens de volledige grafiek door de stippen met een vloeiend lopende lijn te verbinden.
Van dit verband kun je niet zo eenvoudig een formule
geven.
t + @· h = 19
t = -@· h + 19
FORMULES, OUDE EN NIEUWE
2
Ribben, hoekpunten, grensvlakken
We bekijken een n-zijdig prisma (n
is een geheel getal, n ≥ 3). Het
aantal ribben noemen we r, het
aantal hoekpunten h en het aantal
grensvlakken g.
Bij een vijfzijdig prisma is n = 5.
r = 15
h = 10
g = 7
r = 3n
h = 2n
g = n + 2
» Hoe groot zijn r, h en g dan ?
Nu voor een willekeurig n-zijdig prisma.
» Geef formules voor r, h en g, uitgedrukt in n.
Prijsverlaging
In een kledingwinkel worden de prijzen tijdens de opruiming 25% verlaagd.
» Wat kost in de opruiming een jasje dat normaal
€ 80 kost?
De normale prijs noemen we x euro en de prijs in de
opruiming y euro. Er is een verband tussen x en y van
de vorm: y = ⋅ x
» Welk getal moet er op de invulstreep staan?
€ 60
y = H x
De omtrek van een cirkel
De omtrek van een cirkel kun je berekenen door zijn
diameter te vermenigvuldigen met π (dat is ongeveer
3,14). De straal van een cirkel noemen we r, de omtrek p.
» Geef een formule voor p, uitgedrukt in r.
Leeftijd en geboortejaar
Ivette is in 2005 x jaar geworden. Haar geboortejaar
noemen we y.
r
p = 2πr
y = 2005 – x
» Geef een formule voor y, uitgedrukt in x.
Een klassenavond
De feestcommissie van klas K3b heeft inkopen gedaan voor de klassenavond. Ze heeft a flessen sinas
van € 0,90 per stuk gekocht, b flessen cola van € 0,80
per stuk en c flessen 7-up van € 1,10 per stuk. In totaal moest ze hiervoor precies € 50,-- betalen.
» Geef een formule voor a, b en c in de vorm:
⋅ a + ⋅ b + ⋅ c = .
0,9x + 0,8y + 1,1z = 50
diameter
VERBANDEN IN RECHTHOEKEN
333
Rechtenhoeken met gegeven omtrek
Van een rechthoek noemen we de basis b en de
hoogte h (beide in cm).
» Bereken de omtrek (dat is de lengte van de rand)
als b = 6 en h = 4.
20
» Geef een voorbeeld van een andere rechthoek met
dezelfde omtrek.
basis = 5
; hoogte = 5
.
Bij alle rechthoeken met omtrek 20 (cm) is er een
verband tussen de basis b en de hoogte h.
» Vul een tabel in bij dit verband.
61
2
9
6
Een formule bij het verband is 2b + 2h = 20 .
» Druk h uit in b door de formule anders te schrijven.
h = 10 – b
» Teken de grafiek van het verband in het rooster
onderaan de bladzijde. Schrijf het getal 20 bij de
grafiek.
Ook bij rechthoeken met omtrek 10 (cm) bestaat er
een verband tussen de basis b en de hoogte h.
» Geef een formule voor dit verband.
h = 5 – b of 2h + 2b = 10 of…
» Teken de bijbehorende grafiek; schrijf er het getal
10 bij.
» Teken ook de grafieken die horen bij: omtrek 4,
omtrek 8, omtrek 15 en omtrek 24. Schrijf bij elke
grafiek het passende getal.
Je hebt nu zes grafieken getekend. Ze hangen samen:
bij elke grafiek hoort een omtrek. Zo’n serie samenhangende grafieken in één figuur noemt men wel een
nomogram.
24
20
15
4
10
8
8
91
VERBANDEN IN RECHTHOEKEN
444
Rechthoeken met gegeven oppervlakte
Een rechthoek van 4 bij 6 cm heeft oppervlakte 24
cm2. Er bestaan veel rechthoeken met deze oppervlakte.
» Geef drie voorbeelden.
3bij 8; 2 bij 12; 5 bij 4K
Bij alle rechthoeken met oppervlakte 24 is er een verband tussen de basis b en de hoogte h.
» Vul een tabel in bij dit verband.
3
1
2
» Geef een formule van dit verband.
4
h ⋅ b = 24
» Teken de bijbehorende grafiek; schrijf er het getal
24 bij .
24
18
12
6
» Geef ook een formule voor b en h bij oppervlakte
18.
» Teken de bijbehorende grafiek; schrijf er het getal
18 bij.
» Teken ook de grafieken bij oppervlakte 6, bij oppervlakte 12 en bij oppervlakte 30; schrijf bij elke
grafiek het passende getal.
Elk van de grafieken is een (halve) hyperbool.
Het totale plaatje is weer een nomogram.
h ⋅ b = 18
30
16
4K
VERBANDEN IN RECHTHOEKEN
555
Rechthoeken waarbij de verhouding hoogte:basis
steeds hetzelfde is
We bekijken alle rechthoeken waarvan de hoogte
twee keer zo groot is als de basis.
41
10
» Vul een tabel in bij dit verband.
» Geef een formule van dit verband.
23
15
3
h = 2 ⋅ b
» Teken de grafiek van dit verband; schrijf er het getal 2 bij.
» Teken ook de grafieken van de verbanden: h = 5b
, h = 3b , h = b , h = 1b , h = 2b en h = 4b ; schrijf er
de getallen 5, 3, 1, 1 , 2 en 4 bij.
5
3
2
1
2
4
Combineren
Hiernaast zijn de grafieken getekend van de drie verbanden.
• omtrek 26
• oppervlakte 24
• hoogte = 2 × basis
hoogte = 2
basis
hoogte× = 2×basis
In het plaatje is aangegeven welke grafiek hoort bij
hoogte = 2 × basis.
» Geef ook aan welke grafiek hoort bij omtrek 26 en
welke hoort bij oppervlakte 24.
Uit het plaatje kun je de afmetingen aflezen van
• de rechthoek met omtrek 26 en oppervlakte 24
en
• van de rechthoek met oppervlakte 24 en hoogte
2 x de basis
» Doe dat zo nauwkeurig mogelijk en schrijf het resultaat hiernaast op.
omtrek 26
oppervlakte 24
h = 10,8 ; b = 2,2 .
h = 3,5 ; b = 7,0 .
de basis is een zeker getal;
Van de rechthoek met omtrek 26 en hoogte 2 x de basis kun je de basis precies berekenen.
Dat kan bijvoorbeeld zoals hiernaast.
de omtrek is dan 6 ⋅ dat getal;
» Maak de berekening af.
dat getal is dus: 26:6 = 42
de hoogte is dan 2 ⋅ dat getal;
KETTINGEN
6
Machientjes
In de eerste klas heb je kennis gemaakt met machientjes, bijvoorbeeld het machientje KWAD, dat alle getallen die ingevoerd worden kwadrateert.
Andere voorbeelden zijn:
PLUS 2
verhoogt de invoer met 2 ;
MAAL -3
vermenigvuldigt de invoer met -3 ;
WORTEL
trekt de wortel uit de invoer ;
OMG
neemt het omgekeerde van de invoer;
TEGEN
neemt het tegengestelde van de invoer.
-3
Bijvoorbeeld bij
x
De invoer noemen we meestal x en de uitvoer y.
Er is een verband tussen de invoer x en de uitvoer y,
» Geef een formule voor de invoer x en de uitvoer y
bij de andere vijf hierboven genoemde machientjes. (Bij OMG is het verband al gegeven.)
y
KWAD
is een formule: y = x2
PLUS 2
y = x + 2
MAAL -3
y = -3x
WORTEL
y = √x
OMG
TEGEN
Twee kettingen
We kunnen ook kettingen van machientjes maken.
Hiernaast is zo'n ketting getekend.
» Ga na dat de uitvoer 13 is bij invoer 5.
9
KWAD
MAAL 2
y = 1
x
y = -x
PLUS 3
2 ⋅ 5 + 3 = 13
» Geef een formule voor de invoer x en de uitvoer y
bij deze ketting.
y = 2x + 5
Deze ketting bestaat uit twee ‘stappen’. De tussenstap is ‘2x’.
x
MAAL 2
2x
PLUS 3
2x + 3
Bekijk de ketting:
x
PLUS 3
MAAL 2
» Wat moet er op de eerste invulstreep staan en wat
op de tweede?
x + 3
» Wat is een formule voor de invoer x en de uitvoer y
bij deze ketting?
y = 2(x + 3)
2(x + 3)
KETTINGEN
7
Op de vorige bladzijde heb je de twee kettingen hiernaast bekeken. De formules voor y en x bij die twee
zijn verschillend. Als het goed is, heb je ook twee verschillende formules opgeschreven!
Twee andere kettingen vergeleken
Hiernaast staan twee andere kettingen.
De eerste ketting geeft bij invoer 2 de uitvoer 16, de
tweede geeft bij invoer 2 de uitvoer 8. De formules
voor de invoer x en de uitvoer y zijn dus verschillend.
» Geef een formule van elk van de twee kettingen.
y = (2x)2
Nog twee kettingen vergeleken
Bekijk de twee kettingen hiernaast. De invoer is weer
x en de uitvoer y.
» Ga na of de formules voor y en x bij de twee kettingen hetzelfde is. Licht je antwoord toe.
» Geef een formule voor elk van de kettingen.
MAAL 2
PLUS 3
PLUS 3
MAAL 2
MAAL 2
KWAD
KWAD
MAAL 2
of y = 4x2
y = 2x2
PLUS 3
KWAD
KWAD
PLUS 3
Nee, want de eerste geeft bijvoorbeeld bij
invoer 1 uitvoer 16 en de tweede geeft bij invoer 1 uitvoer 4
y = (x + 3)2
y = x2 + 3
Waarschijnlijk heb je bij één van de twee formules
haakjes gebruikt.
» Schrijf die formule zonder haakjes, zo eenvoudig
mogelijk.
» Bereken alle mogelijke waarden (ook negatieve)
die x kan hebben als:
x
PLUS 3
KWAD
y = (x + 3)2 = x2 + 6x + 9
dan:
x + 3 = 12 of x + 3 = -12
dus
x = 9 of x = -15
144
Schrijf je berekening hiernaast netjes op
» Bereken ook alle mogelijke waarden die x kan hebben als:
x
KWAD
PLUS 3
Schrijf je berekening hiernaast netjes op
197
dan: x2 = 194, dus x = √194 of x = -√194
VERBANDEN IN DE PRAKTIJK
8
Remweg
Als een auto uit alle macht remt, staat hij nog niet
meteen stil. De afstand die hij nog aflegt, nadat het
rempedaal is ingedrukt, noemt men de remweg. Hoe
groot de remweg is, hangt af van de snelheid waarmee de auto rijdt.
Met het blokschema hiernaast kun je bij een gegeven snelheid de remweg uitrekenen.
De snelheid noemen we v (in km/u), de remweg r (in
meters).
START
Neem de snelheid in km/uur.
Deel dit getal door 10.
Kwadrateer de uitkomst.
Vermenigvuldig het kwadraat met H .
De uitkomst is de remweg in meters.
KLAAR
» Bereken de remweg bij elk van de snelheden in de
tabel.
12
48
75
147
192
300
We zoeken een formule voor het verband tussen v en
r. Dat kun je bijvoorbeeld doen door een ketting van
machientjes bij het blokschema te maken, waarbij de
invoer v is en de uitvoer r.
v
MAAL /
/v
KWAD
(/v)2
» Vul de passende machientjes en de tussenuitkomsten in.
» Welke formule vind je voor het verband tussen v
en r?
» Laat zien dat je die formule ook kunt schrijven als:
3v 2
.
r=
400
» Teken de grafiek van het verband.
r = H ⋅ H ⋅ (/v)2
(/v)2 = H ⋅ @v2 = 3v 2
400
MAAL H
H ⋅ (/v)2
VERBANDEN IN DE PRAKTIJK
9
Op de autosnelwegen in Nederland is de maximale
toegestane snelheid 120 km/u. Een auto is geslipt en
in de berm terecht gekomen. De politie wil weten of
de automobilist te hard gereden heeft en meet het
remspoor: 105 meter.
» Lees uit de grafiek de snelheid van de auto af.
» Ga door een berekening na of de door jou
afgelezen snelheid precies goed is.
117 km/u
3 ⋅ 1172 : 400 ≈ 103 < 105, dus 117 is te klein.
Celsius en Fahrenheit
Op een thermometer staan vaak twee schaalverdelingen: die van Celsius en die van Fahrenheit. Wij gebruiken eigenlijk alleen maar de schaal van Celsius; in
Engeland en de VS gebruikt men meestal de schaal
van Fahrenheit.
De Zweed Anders Celsius en de Duitser Gabriël Fahrenheit waren
natuurkundigen in de achttiende eeuw. Het was toen nog moeilijk
om temperaturen nauwkeurig te meten. Beiden hebben een thermometer ontworpen.
Graden Celsius wordt afgekort met °C, graden Fahrenheit met °F.
» Welke temperatuur geeft de thermometer hiernaast aan in graden Celsius? En in graden Fahrenheit?
0 °C komt overeen met 32 °F; 100 °C met 212 °F.
» Hoeveel °F komt dus overeen met 50 °C?
Met behulp van het blokschema hiernaast kun je elke
temperatuur omrekenen van °C naar °F.
Het aantal graden Celsius noemen we c, het aantal
graden Fahrenheit f.
29 °C
84 °F
Het gemiddelde van 32 en 212, dus 122°F
START
Neem de temperatuur in °C.
Vermenigvuldig die met 1,8.
Tel er dan 32 bij op.
De uitkomst is de temperatuur in °F.
KLAAR
» Controleer of het blokschema klopt voor 0 °C, voor
50 °C en voor 100 °C. Reken ook de drie andere
temperaturen in de tabel om naar °F.
-40
32
122
212
284
392
VERBANDEN IN DE PRAKTIJK
» Geef een formule voor het verband tussen c en f.
10
f = 1,8c + 32
» Teken de grafiek van het verband.
Inhoud en oppervlakte van een kubus
» Bereken de inhoud en de totale oppervlakte van
een kubus met ribbe 2 cm.
Opmerking
“ribbe 2 cm” betekent dat de ribben 2 cm lang zijn.
De ribbe van een kubus noemen we r (cm), de inhoud
i (cm3) en de totale oppervlakte a (cm2).
» Geef een formule voor het verband tussen r en i.
En van het verband tussen r en a.
i = r3
a = 6 ⋅ r2
» Teken van beide verbanden de grafiek. Maak
eventueel een tabel op klad.
» Lees uit de grafiek af wat de ribbe ongeveer is, als
de inhoud 20 cm3 is.
» Lees uit de grafiek af wat de ribbe ongeveer is, als
de totale oppervlakte 20 cm2 is.
» Geef ook een berekening van de ribbe als de
totale oppervlakte 20 cm2 is.
2,7 cm
1,8 cm
6 ⋅ r2 = 20, dus r2 = 3,333, dus r = √3,333
dus r≈1,83
VERBANDEN IN DE PRAKTIJK
11
Een auto huren
Anneke verhuist van Wageningen naar Amsterdam.
daar gaat ze studeren. Voor de verhuizing heeft haar
vader een Ford Transit (8,5 m3 laadruimte) gehuurd
bij verhuurbedrijf Roelofs. Dat kost € 60,--. De eerste
100 km zijn vrij; die zijn als het ware in het vaste bedrag van € 60,-- verrekend. Voor elke kilometer daarboven moet 30 cent betaald worden.
Annekes vader hoeft maar één keer heen en terug te
rijden van Wageningen naar Amsterdam. De afstand
Wageningen-Amsterdam is 80 km.
» Bereken wat Annekes vader voor de retourrit bij
Roelofs moet betalen.
» Maak een tabel voor het verband tussen het te rijden aantal km a en de kosten k (in euro’s).
60 + 60 ⋅ 0,30 = 78 euro
60
60
60
75
78
90
105
» Teken de grafiek van het verband.
» Beschrijf het verband met formules; onderscheid
twee gevallen.
» Bij welk aantal kilometers kost de huurauto in totaal bij Roelofs € 99,-- ?
Schrijf je berekening op.
In alle voorbeelden speelden twee variabelen een
rol. Steeds was er een verband tussen de variabelen. Een ander woord voor verband is relatie of
betrekking.
Bij een verband horen drie dingen:
• een formule
• een tabel
• een grafiek.
Als a ≤ 100, dan k = ___
60
Als a > 100, dan k = ___
60 + 0,3 ⋅ ( ______
a – 100 )
↑
↑
voor de eerste
boven de
100 km
100 km
Voor het aantal km boven de 100 wordt 99 –
60 = 39 euro betaald. Voor 39 euro kun je
39:0,3 = 130 km rijden.
Dus bij 230 km
VERBANDEN IN HET VLAK
12
We bekijken de punten in het vlak waarvoor geldt:
“De tweede coördinaat is 1 groter dan de helft van de
eerste coördinaat”.
» Maak een bijbehorende tabel:
-2
-1
1
21
4
51
» Teken de bijbehorende punten in het assenstelsel.
Deze punten liggen op een rechte lijn. De eerste coördinaat van de punten noemen we x, de tweede coördinaat noemen we y. De cursieve zin hierboven legt
een verband vast tussen x en y.
» Geef een formule voor dit verband.
» Bereken met de formule welk getal x is, als y = 100
» En welk getal is y, als x = 100 ?
y = 1x + 1
100 = 1x + 1, dus1 x = 99,dus x = 198
y = 1 ⋅ 100 + 1 = 51
We zeggen dat de punten (100,51) en (198,100) voldoen aan het verband. Deze punten liggen op de grafiek.
» Ga met de formule na welke van de volgende punten aan het verband voldoen:
(-B , B), (41 , 3 ) , (-10 , -6) , (2K , 24).
Afspraak
De eerste coördinaat van punten in een assenstelsel noemen we in de regel x , de tweede coördinaat noemen we y.
B = 1 ⋅ B + 1 ? NEE
3 = 1 ⋅ 41 + 1 ? NEE
-6 = 1 ⋅ -10 + 1 ? NEE
24 = 1 ⋅ 2K + 1 ? NEE
VERBANDEN IN HET VLAK
13
De som van de coördinaten is -3
We bekijken het verband: “De som van de coördinaten is -3”.
» Geef een formule van dit verband.
x + y = -3
» Maak een tabel bij dit verband.
-2
0
2
4
6
8
-1
-3
-5
-7
-9
-11
» Teken de grafiek van dit verband.
» Welk punt dat aan het verband voldoet, heeft gelijke eerste en tweede coördinaat?
(-11,-11)
De tweede coördinaat is 5 minder dan het kwadraat van de eerste coördinaat
We bekijken het verband: “De tweede coördinaat is 5
minder dan het kwadraat van de eerste coördinaat”.
» Geef een formule van dit verband.
» Maak een tabel bij dit verband.
y = x2 – 5
-3
-2
-1
0
1
2
4
-1
-4
-5
-4
-1
» Teken de grafiek in het assenstelsel hierboven.
Gebruik een (andere) kleur. Dat is een parabool.
» Bereken x, als y = 13 (twee antwoorden!)
13 = x2 – 5, dus x2 = 63, dus x = 21 of x = -21
Op deze pagina hebben we twee verbanden bekeken.
(-2,-1) en (1,-4), (dat zijn de snijpunten van
de twee grafieken)
» Welke punten voldoen aan beide verbanden?
VERBANDEN IN HET VLAK
14
x ⋅ y = -6
We bekijken het verband met formule x ⋅ y = -6.
» Beschrijf dit verband in woorden. Gebruik de woorden “eerste coördinaat” en “tweede coördinaat”.
het product van de eerste en de tweede coordinaat is -6
» Maak een tabel bij dit verband; kies zowel positieve als negatieve getallen voor x.
-3
2
-2
3
-1
6
0
–
1
-6
2
-3
» Teken de grafiek van dit verband (dat is een hyperbool).
Er is een punt dat aan het verband voldoet, met eer6
.
ste coördinaat 11
» Bereken de tweede coördinaat. Schrijf ook je berekening op.
6 ⋅y
11
= −6 , dus y = -6 ⋅ 11/6 = -11
Er is ook een punt dat aan het verband voldoet, met
eerste coördinaat 2 52 .
» Bereken de tweede coördinaat. Schrijf je berekening weer op.
22/5 ⋅ y = -6, dus y = -6 ⋅ 5/12 = -21/2
Op één uitzondering na is er voor elk getal x is er een
getal y te vinden met x ⋅ y = -6.
» Welk getal is die uitzondering?
0
x+y=5
We bekijken het verband met formule: x + y = 5 .
» Maak een tabel bij dit verband.
-2
-1
0
1
2
7
6
5
4
3
» Teken de grafiek in het assenstelsel hierboven.
Gebruik een (andere) kleur.
Gemeenschappelijk
» Voor welke punten (x,y) geldt:
x ⋅ y = -6 en x + y = 5?
Je kunt de coördinaten van die punten aflezen.
Controleer met de formules of je dat goed gedaan
hebt.
Zo te zien (6,-1) en (-1,6). En dat klopt, want:
voor beide punten geldt:
het product van de coördinaten is -6;
de som van de coördinaten is 5.
VERBANDEN IN HET VLAK
Grafiek maken bij een blokschema
Het blokschema hiernaast legt een verband vast in
het vlak.
Pas op: In het derde blok moet je doen: ‘ 8 : ___ ‘ en
niet ‘
:8 ’.
15
START
Neem de eerste coördinaat.
Tel er 2 bij op.
Deel 8 door de uitkomst.
De uitkomst is de tweede coördinaat.
KLAAR
» Maak een tabel bij dit verband.
-4
Als je voor de eerste coördinaat -2 neemt, krijg je
geen tweede coördinaat.
» Waarom niet?
» Laat het blokschema werken op de variabele x.
Welke formule vind je dan voor x en y?
-4
-8
4
2
Je kunt 8 niet delen door 0.
y = 8 : (x + 2)
» Teken de grafiek van dit verband (een hyperbool).
» Bereken met de formule y, als x = -11 en als
x = -21.
y = 8/1 = 16
y = 8/-1 = -16
» Bereken met de formule x, als y = 1 en als y = -1.
8:(x + 2) = 1, dus
8:(x + 2) = -1, dus
x + 2 = 16, dus
x = 14
x + 2 = -16, dus
x = -18
1
VERBANDEN IN HET VLAK
16
Grafiek maken bij een ketting
De ketting hieronder legt een verband vast in het vlak.
De invoer noemen we x en de uitvoer y.
MIN 3
MAAL 2
PLUS 5
-3
» Maak een tabel bij dit verband.
» Geef een formule voor het verband tussen x en y.
Schrijf de formule ook zonder haakjes en zo eenvoudig mogelijk.
-1
1
3
5
7
2
1
y = 2(x – 3) + 5 = 2x – 6 + 5 = 2x – 1
Dus y = 2x – 1
» Teken de grafiek van het verband.
Opmerking
De hele grafiek is een rechte lijn, naar twee kanten
onbegrensd. Jij hebt natuurlijk alleen dat deel van de
lijn getekend dat op het stukje rooster paste.
Ook in vorige opgaven heb allen maar het deel van de
grafiek getekend dat in het rooster paste
Op de lijn liggen punten met tweede coördinaat 17 en
-17.
»
Bereken de eerste coördinaat van deze punten.
Nog een ketting
De ketting hieronder heeft als grafiek ook een rechte
lijn.
MIN 4
TEGEN
PLUS 1
2x – 1 = 17
2x – 1 = -17
2x = 18
2x = -16
x = 9
x = -8
y = -(x – 4) + 1 = -x + 4 + 1 = -x + 5
Dus: y = -x + 5
» Geef een formule voor deze tweede lijn. Schrijf die
ook zonder haakjes zo eenvoudig mogelijk.
» Maak een tabel bij dit verband.
» Teken de grafiek van het verband in het rooster
hierboven.
» Kun jij zo zien wat de oplossing is van de vergelijking –x + 5 = 2x – 1? Licht je antwoord toe.
6
5
4
3
x = 2, want de vraag is:'Voor welke eerste coordinaat is de de tweede coördinaat bij de
eerste ketting hetzelfde als die van de tweede ketting?' En dat is de x van het snijpunt.
VERBANDEN IN HET VLAK
Enkele merkwaardige verbanden
De volgende zin legt een verband vast in het vlak:
“ Het kwadraat van de eerste coördinaat is gelijk aan
het kwadraat van de tweede coördinaat”.
17
x2 = y2
» Geef een formule van dit verband.
» Welke punten met eerste coördinaat -2 voldoen
aan dit verband?
(-2,2) en (-2,-2)
» Schrijf de formule zó:
x = -y
x = y of _______
» Teken de grafiek van het verband in het assenstelsel hiernaast.
De volgende zin legt een verband in het vlak vast.
‘Verminder de tweede coördinaat met 1 en verminder
de tweede coördinaat ook met 3. Het product van de
twee getallen die je krijgt moet je vermenigvuldigen.’
Merk op dat de eerste coördinaat niet genoemd wordt.
» Voldoet (5,3) aan dit verband? Leg uit.
» Welke van de volgende punten voldoen aan het
verband?
( -4 , 3 ) , ( -41 , 3 ) , (-41 , 1 ) , (-41 , 2)
Ja, want je krijgt na vermindering 2 en 0 en
die twee getallen vermenigvuldigen geeft 0.
( -4 , 3 ) , ( -41 , 3 ) , (-41 , 1 )
» Teken de grafiek van het verband in het rooster
hierboven.
Bovenstaande zin kun je zó opschrijven:
(y−1)(y−3) = 0.
» Schrijf de formule zó:
» Teken met een (andere) kleur de grafiek van het
verband met de formule x2 = 4 .
y = ____
of y = ____
1
3
x = 2____ of x = ____
-2
» Schrijf de formule zó :
» Welke punten voldoen aan beide verbanden tegelijk?
(y−1)(y−3) = 0 en x2 = 4?
(2,3), (2,1), (-2,3), (-2,1)
VERBANDEN IN HET VLAK
18
Cola en bier
Voor zijn feestje haalt Aron cola en bier. De cola zit in
flessen van 11 liter. Hierop is het statiegeld € 0,25. Het
bier zit in flesjes van 30 cl (pijpjes). Hierop is het statiegeld € 0,10.
Het aantal flessen cola dat hij haalt noemen we x en
het aantal flessen bier y.
In totaal haalt hij 30 flessen, daarvoor betaalt hij 6 euro statiegeld.
Er zijn twee verbanden tussen x en y.
» Geef van beide de formule.
x + y = 30
en 0,25 ⋅ x + 0,10 ⋅ y = 6
» Maak van beide verbanden (op klad) een tabel en
teken de grafieken in het assenstelsel.
» Lees af hoeveel flessen cola en hoeveel flessen
bier Aron gekocht heeft.
20 flessen cola en 10 flessen bier
VERBANDEN IN DE RUIMTE
19
Coördinaten in de ruimte
In de ruimte zijn door een punt O, de zogenaamde
oorsprong, drie onderling loodrechte lijnen getekend,
de x-as, y-as en de z-as.
Het punt P bereik je vanuit O door eerst 1 eenheid
naar voren te komen (in de x-richting), dan 4 eenheden naar rechts te gaan (in de y-richting) en tenslotte
3 eenheden naar boven (in de z-richting).
De x-coördinaat van P is 1, de y-coördinaat is 4 en
de z-coördinaat is 3.
We zeggen P = (1, 4, 3).
P
R
S
Q
O
x
» Wat zijn de coördinaten van Q, R en S?
De tweede coördinaat van S is 0.
» Wat kun je zeggen over de ligging van punten met
tweede coördinaat = 0?
En over punten met derde coördinaat 0?
Q( 1
)
, 2 , 1 ), R( 3 , 2 , 1 ), S( 4 , 0 , 2)
die liggen in het vlak door de x-as en de z-as,
(in het 'rechter' zijvlak')
die liggen in het vlak door de x-as en de y-as,
(in het 'grondvlak')
Afspraak
In een ruimtelijk assenstelsel noemen we de eerste coördinaat van een punt in de regel x , de
tweede coördinaat y en de derde coördinaat z.
De oorsprong O is het punt (0,0,0). Meestal tekenen
we de x-as schuin naar voren, de y-as naar rechts en
de z-as naar boven.
De som van de coördinaten
De volgende zin legt een verband vast in de ruimte:
“De som van de coördinaten is gelijk aan zes”.
» Geef een formule voor dit verband.
x + y + z = 6
» Voldoet het punt (1,2,3) aan dit verband?
Ja
y
VERBANDEN IN DE RUIMTE
20
De kubus met ribbe 3 hiernaast heeft drie ribben
langs de coördinaat-assen.
(0,0,0) is dus een van de hoekpunten. Op de kubus
zijn 37 roosterpunten aangegeven.
» Kleur alle van deze roosterpunten die aan het verband x + y + z = 6 voldoen. Dat zijn er 13.
“De som van de coördinaten is gelijk aan zeven”.
Deze zin legt een verband vast in de ruimte.
» Kleur alle roosterpunten hiernaast die aan het verband x + y + z = 7 voldoen.
De eerste en de derde coördinaat zijn gelijk
De volgende zin legt een verband vast in de ruimte:
“De eerste en de derde coördinaat zijn gelijk”.
x = z
» Geef een formule voor dit verband.
» Kleur hiernaast alle van de 37 aangegeven punten
die aan het verband voldoen.
z = 2
» Geef met een andere kleur de punten aan die voldoen aan het verband met formule: z = 2.
» Welke van de 37 roosterpunten voldoet aan beide
verbanden?
Het is duidelijk dat grafieken van verbanden in de
ruimte veel moeilijker te lezen en te maken zijn dan in
het platte vlak. Dat doen we dan ook zelden. Op de
volgende bladzijde doen we een bescheiden poging
om ruimtelijke grafieken te maken.
(2
, 3
, 2
);
VERBANDEN IN DE RUIMTE
21
x + 3y + 2z = 12
We bekijken het verband met formule x + 3y + 2z = 12
We gaan alle roosterpunten tekenen die aan dit verband voldoen met alle drie de coördinaten positief of
nul.
Neem z = 2. Dan zijn er drie mogelijkheden, namelijk
(8,0,2), (5,1,2) en (2,2,2). Controleer maar. Het eerste
punt van deze drie is hiernaast getekend.
» Teken er de andere twee punten bij.
Nu zijn alle drie de punten met z = 2 getekend die aan
het verband voldoen.
» Teken ook de punten met z = 0 die aan het verband voldoen.
En de punten met z = 1, z = 3, z = 4, z = 5 en z = 6.
Als je het goed gedaan hebt, heb je in totaal negentien punten gevonden die aan het verband voldoen
met niet-negatieve coördinaten.
Er zijn natuurlijk ook punten die aan het verband voldoen met een of meer negatieve coördinaten.
» Noem er een paar.
(-1,-1,8) , (-10,0,11) , (20,-2,-1)
» Zijn er ook punten die aan het verband voldoen
met alle drie de coördinaten negatief?
Nee, want dan is x + 3y + 2z ook negatief.
En dan heb je natuurlijk nog vreselijk veel punten die
aan het verband voldoen, waarvan de coördinaten
niet geheel zijn.
» Noem er een paar.
Waarschijnlijk heb je wel in de gaten dat de punten
die aan het verband voldoen niet kriskras door elkaar
liggen. De grafiek is namelijk een perfect plat vlak.
x + y + 2z = 4
Een ander voorbeeld: het verband met formule
x + y + 2z = 4.
» Teken alle roosterpunten met niet-negatieve coördinaten die aan dit verband voldoen.
(10,2,1) , (121,0,-3)
VERBANDEN IN DE RUIMTE
22
x + y + z = 16 en 2x + 3y + z = 32
Hiernaast is een balk van 10 bij 5 bij 5 getekend met
drie ribben langs de assen.
Uit de balk is een hap weggenomen. De 43 roosterpunten die daardoor zichtbaar zijn geworden, zijn dik
aangegeven.
» Kleur alle van deze 43 punten die voldoen aan het
verband x + y + z = 16.
» Welke van deze punten voldoen ook aan het verband 2x + 3y + z = 32?
(10,3,3), (8,4,4), (6,5,5)
» Geef die punten in het plaatje aan.
Voor de punten die aan beide verbanden voldoen,
geldt: x + y + z = 16 en 2x + 3y + z = 32. Die punten liggen op een rechte lijn.
28 van de 43 punten zijn niet gekleurd.
» Hoe groot is de som van de coördinaten x+y+z van
deze punten?
15 of 14
GEMENGDE OPGAVEN
23
Een watertarief
Vroeger (in 1983) hanteerde het waterleidingbedrijf in
Wageningen twee prijzen voor 1 m3 water. Een m3
kostte 59 cent. Ten minste tot en met de 150ste m3. De
151ste m3 kostte 82 cent, en ook elke volgende m3.
» Waarom zou men twee verschillende prijzen gehanteerd hebben, denk je?
Om verspilling af te straffen
Het volledige watertarief voor huishoudelijk gebruik
was als volgt:
• Iedere abonnee betaalde 63 gulden per jaar.
Daar-voor kreeg hij de eerste 60 m3 water. Dat bedrag was een soort vastrecht; dat moest je sowieso betalen.
• De 61ste tot en met de 150ste m3 water kostten alle
59 cent.
• Vanaf de 151ste m3 kostte het water 82 cent per m3.
» Bereken de kosten bij een verbruik van 120 m3 en
bij een verbruik van 180 m3. Schrijf ook je berekeningen op.
63 + 60 ⋅ 0,59 = 98,40
63 + 90 ⋅ 0,59 + 30 ⋅ 0,82 = 140,70
» Maak een tabel bij het verband tussen het verbruik
v (in m3) en de kosten k (in guldens).
63
63
63 80,7 98,4 116,1 140,7 165,3
» Teken de grafiek van het verband.
Om het verband met formules te beschrijven, moet je
drie gevallen onderscheiden.
» Maak de formules af.
•
Als v ≤ 60 , dan k = 63
___
•
Als 60 < v ≤ 150 , dan
k = ____
63 + ____·
0,59 (v − ____
60 )
•
Als 150 < v, dan
k = ____
116,1 + ____·
0,82 (v − ____
150 )
GEMENGDE OPGAVEN
24
Hoe lang een rit van 600 km duurt
Een vakantiereis voert familie de Vrij via Duitse autowegen over een afstand van 600 km. Hoe lang familie
de Vrij over de reis doet, hangt natuurlijk af van de
gemiddelde snelheid waarmee ze rijdt. Met andere
woorden: er is een verband tussen de reistijd en de
gemiddelde snelheid.
» Bereken de gemiddelde snelheid als de reis 8 uur
duurt.
600 / 8 = 75 km/u
» Maak een tabel voor het verband tussen de reistijd
t (in uren) en de gemiddelde snelheid v (in km/u).
» Geef een formule voor dit verband.
200 150 120 100 855/7 75
60 50
v = 600/t
» Teken de grafiek van dit verband.
De Vrij reed het traject vorig jaar met een gemiddelde
snelheid van 110 km/u en vanwege de files dit jaar
met 100 km/u.
» Bereken hoeveel korter hij er vorig jaar over deed.
Rekentechniek
In de vorige vraag heb een breuk van een geheel getal afgetrokken.
r is een CD bij de Wageningse Methode met een programma waarmee je het optellen en aftrekken van
breuken kunt oefenen.
Dat gaat zó
• noemers gelijk maken,
• tellers aftrekken.
» Schrijf als één breuk; schrijf ook een tussenstap
op.
Nu 600/100 = 6 uur
Vorig jaar 600/110 = 55/11 uur
Dus 6/11 uur korter
− 9
9
45
7
9
−
3
5
=
7
8
−
3
5
=
35 _ 24
40 40
−
3
5
=
35 _ 3t
35 _ 3t
= 5t 5t
5t 5t
7
t
10
9
35
45
45
=
= 11
40
35 – 3t
5t
= − 10
= 110 _ 90 = 20
11
99
10
t
−
10
11
10
t
−
10
t +1
99
= 110 _ 10t
11t
11t
99
= 110 – 10t
11t
= 10(t + 1) _
t(t + 1)
10t
t(t + 1)
= 10 t(t + 1)
GEMENGDE OPGAVEN
25
Het juiste gewicht
Wanneer is iemand te zwaar of te licht? Dat hangt natuurlijk af van zijn lengte, maar ook van de dikte van
zijn botten. De lengte noemen we L (in cm) en de omtrek van de pols noemen we P (ook in cm). Het ideale
gewicht G (in kg) kun je dan uitrekenen met de formule: L + 4P = 100 + 2G (voor mannen).
50
70
90
Joris heeft een polsomtrek van 20 cm, is 184 cm lang
en weegt 82 kg.
184 + 4 ⋅ 20 = 100 + 2G geeft: G = 82
Hij heeft precies het goede gewicht.
» Is hij te licht of te zwaar?
» Hoe ziet de formule voor L en P eruit voor mannen
van 50 kg? En voor mannen van 70 kg en 90 kg?
L + 4P = 200
____
L + 4P = 240
» Teken hierboven in kleur de drie bijbehorende grafieken. Schrijf er de getallen 50, 70 en 90 bij.
Door voor G verschillende waarden te nemen, krijg je
een nomogram (zie bladzijde 4).
Ladder
De voet van een ladder wordt op 1 m van de muur
geplaatst. Hoe langer de ladder is hoe hoger hij reikt.
Er is een verband tussen de lengte van de ladder x en
de reikhoogte y (beide in meters).
» Bereken y als x = 10, laat de wortel in je antwoord
staan.
Je kunt een ketting van drie machientjes maken die bij
invoer x (de lengte van de ladder) als uitvoer y (de
reikhoogte) geeft.
1
2
» Wat zijn de machientjes 1, 2 en 3?
3
y2 + 1 = 102, dus y = √99
1 KWAD
2 MIN 1
3 WORTEL
L + 4P = 280
GEMENGDE OPGAVEN
26
Grafieken bij twee verbanden
» Maak voor elk van de volgende verbanden een tabel op klad en teken de grafiek.
Gebruik verschillende kleuren.
• y = 4 − x2
• x=
6
y
Elkaar neutraliserende kettingen
Bekijk de ketting hiernaast.
De invoer noemen we x en de uitvoer y.
PLUS 3
» Geef de formule van het verband tussen x en y.
Schrijf die zonder haakjes zo eenvoudig mogelijk.
y = 1(x + 3) – 2 = 1x + 11 – 2 = 1x – 1 PLUS 2
Hiernaast staat nog een ketting.
» Geef ook bij deze ketting een formule voor het verband tussen de invoer x en de uitvoer y.
MIN 2
MAAL 1
MAAL 2
MIN 3
y = 2(x + 2) – 3 = 2x + 4 – 3 = 2x + 1
We laten nu de twee kettingen achter elkaar werken:
PLUS 3
MAAL 1
PLUS 2
MIN 2
MAAL 2
MIN 3
De invoer bij de ketting van zes machientjes noemen
we x en de uitvoer y.
» Geef een formule voor het verband tussen x en y
» Verklaar de titel van de opgave.
Bekijk de ketting
WORTEL
De ene ketting maakt de werking van de andere ketting weer ongedaan, dus geeft de
oorspronkelijke invoer weer terug.
MIN 2
» Welke ketting neutraliseert deze ketting?
ZELFTOETS
y = x
PLUS 2
KWAD
TERUGBLIK
27
WAT ZIJN VERBANDEN
GRAFIEKEN
Op welke manier kan een verband tussen de
variabelen x en y gegeven worden?
Wat voor soort grafieken heb je gezien?
.
• door een blokschema
• parabool
• door een formule
• hyperbool
• door een ketting
• rechte lijn
• door een grafiek in het Oxy-vlak
TERMINOLOGIE
MACHIENTJES
• oorsprong
Welke standaard-machientjes ken je?
PLUS …
2
PLUS
• nomogram
MIN …
• verband
MAAL …
• x-as / y-as / z-as
WORTEL
OMG
• blokschema
• ketting van machientjes
TEGEN
• punt voldoet aan
COÖRDINATEN IN DE RUIMTE
Geef een paar voorbeelden.
naar boven
O
VERBANDEN IN DE RUIMTE
x + y + z = 15,
hieraan voldoet bijvoorbeeld (4,5,6), maar ook
(-1,-1,17) en (1,1,14).
naar rechts
naar voren
Als je van O naar P moet door x stappen naar
voren, y stappen naar rechts en z stappen
naar boven te gaan, is P = (x,y,z).
2x + y = z,
hieraan voldoet bijvoorbeeld (0,0,0), (1,1,3) en
(-1,-10,-11).
EXTRA OPGAVEN
28
Verband in woorden en verband met blokschema
De volgende zin legt een verband vast: “De som van
het tegengestelde van de eerste coördinaat en het
dubbele van de tweede coördinaat is gelijk aan 4”.
» Geef een formule van het verband.
-x + 2y = 4
» Teken de grafiek van het verband.
Maak zo nodig een tabel op klad.
verband in
woorden
lijn van punten
met gelijke xen ycoördinaat
» Welk punt voldoet aan het verband en heeft gelijke
coördinaten?
grafiek bij
blokschema
(4,4)
Het blokschema hiernaast legt een verband vast.
START
Neem de eerste coördinaat.
Vermenigvuldig die met -2.
Tel er 7 bij op.
Deel door -2.
De uitkomst is de tweede coördinaat.
KLAAR
» Teken in het assenstelsel hierboven de grafiek van
dit verband. Gebruik een (andere) kleur.
» Geef een formule van dit verband. Schrijf de formule zonder haakjes en zo eenvoudig mogelijk.
» Welk punt voldoet aan beide verbanden?
y = (-2x + 7):-2 = x – 31
(11,71)
EXTRA OPGAVEN
29
De wet van Boyle
In een holle cilinder zit een zekere hoeveelheid gas,
afgesloten door een zuiger. Als de zuiger omlaag beweegt, wordt het volume van het gas kleiner en de
druk groter. Veronderstel dat bij een volume van 1
dm3 het gas een druk heeft van 100 kiloPascal.
Uit de natuurkunde ken je de wet van Boyle. Die geeft
het verband tussen het volume V (in dm3) en de druk
p (in kPa) bij gelijkblijvende temperatuur: p·V = 100.
» Teken de grafiek van dit verband.
Maak zo nodig een tabel op klad.
» Weet jij een naam voor deze grafiek?
Kansen met twee dobbelstenen
Inette gooit met een rode en een blauwe dobbelsteen.
Het aantal ogen dat ze met de rode dobbelsteen gooit
noemen we x en het aantal dat ze met de blauwe
gooit noemen we y.
Het omcirkelde roosterpunt komt overeen met de
worp 4 met de rode en 3 met de blauwe dobbelsteen.
We bekijken het verband tussen x en y: de som van
de ogen is 7.
hyperbool
y
6
som is 7
5
dubbel
4
3
2
1
1
» Kleur de roosterpunten bij het verband.
2
» Geef een formule voor het verband.
x + y = 7
» Wat is de kans dat Inette met twee dobbelstenen
in totaal 7 ogen gooit?
6 op 36 dus: 5
Een ander verband wordt gegeven door: er wordt
dubbel gegooid.
» Kleur de roosterpunten bij het verband.
» Geef een formule voor het verband.
x = y
3 4
5
6
x
EXTRA OPGAVEN
30
Kansen met drie dobbelstenen
Ivo heeft twee abnormale en één gewone dobbelsteen, een rode, een witte en een blauwe. Hieronder
zie je uitslagen van de drie stenen.
Het aantal ogen dat met de rode dobbelsteen gegooid
wordt noemen we x, het aantal dat met de witte gegooid wordt y en het aantal dat met de blauwe gegooid wordt z.
Elke stip in het rooster stelt een worp voor. De pijl
wijst naar de stip die hoort bij de worp 2 ogen met de
rode, 1 oog met de witte en 3 met de blauwe.
» Kleur de punten bij het verband: met de blauwe
twee keer zoveel ogen als met de witte.
z = 2y
x + 2y + z = 8
fout:
het aangewezen punt is: (3,1,3)
z = 2y
» Welke formule hoort hierbij?
» Hoeveel verschillende worpen zijn er mogelijk?
Wat is de kans op met de blauwe twee keer zoveel
ogen als met de witte?
in totaal: 2 ⋅ 3 ⋅ 6 = 36
met z = 2y: 6
5
In een spel is het aantal punten dat je bij een worp
haalt, het totale aantal ogen op de stenen waarbij die
op de witte dubbel geteld moeten worden. Dus bij de
worp (1,2,3) heb je 8 punten.
» Welke formule hoort bij het verband: het aantal
punten is 8 ?
x + 2y + z = 8
» Kleur (in een andere kleur) de roosterpunten bij het
verband het aantal punten is 8.
» Wat is de kans dat je 8 punten haalt bij een worp
met de drie stenen?
5
Twee kettingen
KWAD
MAAL 3
MAAL 3
KWAD
PLUS 1
de eerste:
y = 3x2 + 1
de tweede:
y = (3x)2 + 1 = 9x2 + 1
PLUS 1
» Geef van beide kettingen een formule voor het
verband tussen de invoer x en de uitvoer y.
Schrijf beide formules zonder haakjes en zo eenvoudig mogelijk.
EXTRA B
Kanteldeur
Een kanteldeur is 2 meter hoog. De bovenkant wordt
geleid langs een horizontale rail, de onderkant langs
een verticale rail. Hierboven zijn twee standen van de
deur getekend.
De deur is dicht. Als we de onderkant van de deur x dm naar
boven schuiven gaat de bovenkant y dm naar achteren.
» Geef een formule voor het
verband tussen x en y.
(20 – x)2 + y2 = 400
» Maak een tabel voor het verband.
12
» Teken de grafiek van dit verband in het assenstelsel boven aan de bladzijde.
Twee verbanden vergeleken
In deze opgave bekijk je tweetallen getallen die opgeteld dezelfde uitkomst geven als vermenigvuldigd.
Een voorbeeld is 3 en 11 (in beide gevallen is de uitkomst 41). We noemen deze getallen x en y.
» Welke formule geldt voor x en y ?
» Bereken x, als y = 4.
Bereken y, als x = -1.
De volgende zin legt een verband vast tussen twee
getallen: “De som van de omgekeerden van de getallen is 1”.
Noem de getallen weer x en y.
» Welke formule geldt voor x en y?
» Laat zien dat de twee formules op hetzelfde neerkomen.
16
18,3
19,6
20
x + y = x ⋅ y
x + 4 = 4x
-1 + y = -y
3x = 4
-1 = -2y
x = 12
y = 1
1 + x 1 = 1
y
xy ⋅ 1 = y en xy ⋅ 1 = y, dus als je beide kanten
x y
van het laatste verband met xy vermenigvuldigt, krijg je: y + x = xy
EXTRA B
Hiernaast staat een balk van 4 bij 4 bij 6 met drie ribben langs de assen.
De punten die voldoen aan het verband 4x – y + 2z = 8
liggen in een vlak V. Het stuk van V dat binnen de
balk ligt of op de rand ervan, is een vierhoek. Die
vierhoek is getekend.
Het hoekpunt rechts onder van de vierhoek is (3,4,0).
» Ga door een berekening na dat dat punt inderdaad
aan het verband 4x – y + 2z = 8 voldoet.
4 ⋅ 3 − 4 + 2 ⋅ 0 = 8 , klopt
» Geef de andere drie hoekpunten van de vierhoek.
Gebruik de formule van het verband.
(2,0,0) , (0,0,4) , (0,4,6)
De punten die voldoen aan het verband x + y + z = 3
liggen in een vlak W. Het stuk van W dat binnen de
balk ligt of op de rand ervan is een driehoek.
»
Kleur die driehoek.
De punten die zowel tot V als tot W behoren liggen op
een lijn. Dat is de zogenaamde snijlijn van V en W.
» Teken die snijlijn.
Er is maar één roosterpunt (dus met gehele coördinaten) op de snijlijn met positieve coördinaten of nul.
» Probeer dit roosterpunt te vinden.
(1,0,2)