ongelijkheden - Project X 2002

Extra opgaven: ongelijkheden & ligging van de wortels
1. Los de ongelijkheid algebraïsch op:
3x2  2 x 1  2 x2  4 x  3 ()
2. (Toets ’07-’08) Los de ongelijkheid algebraïsch op:
 x  3  5  6 x  x 2 
x2  2
 0 ()
 x 2  3 x  2

1
3. (Toets ’07-’08) Los het volgende stelsel ongelijkheden algebraïsch op:  x  3  0
()
2
2 x 2  12  5 x
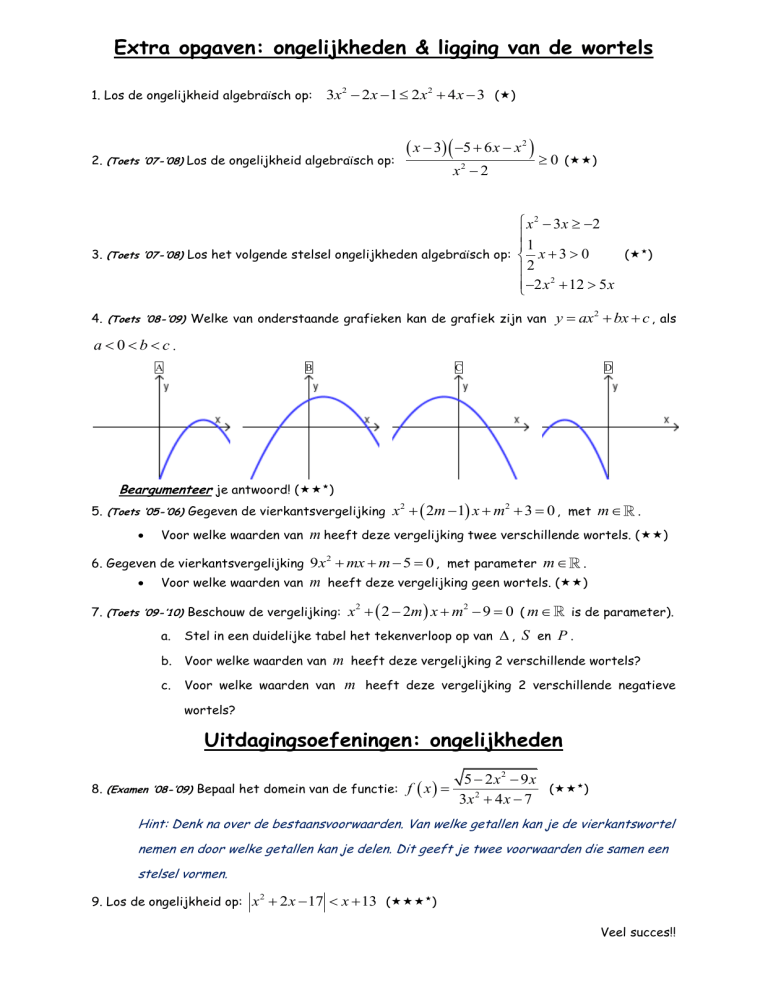
4. (Toets ’08-’09) Welke van onderstaande grafieken kan de grafiek zijn van
y  ax 2  bx  c , als
a0bc.
A
B
C
D
Beargumenteer je antwoord! ()
5. (Toets ‘05-’06) Gegeven de vierkantsvergelijking

Voor welke waarden van
x2   2m  1 x  m2  3  0 , met m .
m heeft deze vergelijking twee verschillende wortels. ()
6. Gegeven de vierkantsvergelijking 9 x  mx  m  5  0 , met parameter
2

Voor welke waarden van
m heeft deze vergelijking geen wortels. ()
7. (Toets ’09-’10) Beschouw de vergelijking:
a.
x 2   2  2m  x  m2  9  0 ( m
Stel in een duidelijke tabel het tekenverloop op van  ,
b. Voor welke waarden van
c.
m .
is de parameter).
S en P .
m heeft deze vergelijking 2 verschillende wortels?
Voor welke waarden van
m heeft deze vergelijking 2 verschillende negatieve
wortels?
Uitdagingsoefeningen: ongelijkheden
8. (Examen ’08-’09) Bepaal het domein van de functie:
f  x 
5  2 x2  9 x
()
2
3x  4 x  7
Hint: Denk na over de bestaansvoorwaarden. Van welke getallen kan je de vierkantswortel
nemen en door welke getallen kan je delen. Dit geeft je twee voorwaarden die samen een
stelsel vormen.
9. Los de ongelijkheid op: x  2 x  17  x  13 ()
2
Veel succes!!
Oplossingen:
1)
V  3  7,3  7 
2)
V   ,  2   1, 2   3,5
3)
V  4,1
4) B, want S  
b
c
 0 en P   0  Er zijn twee wortels (nulpunten) met een
a
a
verschillend teken waarvan de positieve in absolute waarde groter is dan de negatieve.
11
4
5)
m
6)
m  6,30
7) a. Tekenverlopen:
5

+
0
-
+
+
+
+
0
+
+
+
x

3

+
+
+
+
+
+
S
-
-
-
0
+
P
+
0
-
-
-
b.
m ,5
c.
m , 3
1
8)
7   7 1 

dom f   5,    , 
3   3 2

9)
V  6, 4  1,5
3