V b ld J Voorbeeld Java

V
Voorbeeld
b ld Java-programma
J
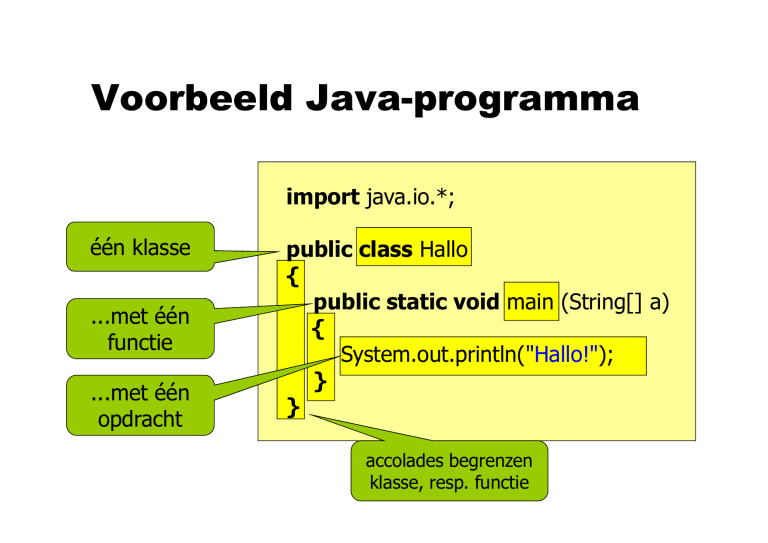
import java.io.*;
één klasse
...met één
functie
...met
met één
opdracht
public class Hallo
{
public static void main (String[] a)
{
System.out.println("Hallo!");
}
}
accolades
l d begrenzen
b
klasse, resp. functie
S
Soorten
t
opdrachten
d
ht
 Toekennings -opdracht:
verander
d het
h t geheugen
h
 Aanroep
p van een andere methode:
voer eerst de opdrachten in die methode uit,
en ga daarna verder waar je gebleven was
en dat kunnen zelf ook weer aanroepen
zijn van weer andere methodes...
d de
dus
d “waar
“
was ik gebleven”
bl
” administratie
d i i
i is
i best
b
ingewikkeld!
i
ikk ld
S t
Syntax
van opdracht
d
ht
opdracht
object
.
functie
naam
expressie
(
,
variabele
=
expressie
;
)
;
Functies definiëren
en ffuncties
ti
aanroepen
public static void printKwadraat (int x)
{ int kw;;
kw = x*x;
System.out.println( x + " kwadraat is " + kw );
}
public
bli static
t ti void
id main
i (String[]
(St i [] a))
{ printKwadraat(2);
printKwadraat(3);
Aanroep
printKwadraat(10);
van een functie
}
voert opdrachten uit
in de body daarvan
F
Functies
ti
mett een resultaat
lt t
public static int kwadraat (int x)
{ int kw;;
kw = x*x;
return kw;
}
public
bli static
t ti void
id main
i (String[]
(St i [] a))
{
System.out.println( "kijk: " + kwadraat(2) );
System.out.println( kwadraat( kwadraat(5) ) );
}
S t
Syntax
van methode-definitie
th d d fi iti
functie
definitie
public
private
i t
type
static
functie
naam
(
par-decl
,
void
{
)
opdracht
declaratie
}
P bli k
Publieksvraag
Definieer een functie driewerf
di je
die
j zo kunt
k t aanroepen:
public static void main (String[] a)
{
System out println( driewerf ("Hoera!")
System.out.println(
( Hoera! ) );
}
D i
Driewerf-functie
ff
ti
Definieer een functie driewerf
di je
die
j zo kunt
k t aanroepen:
declaratie van
public static String driewerf (String x)
{ String res;
res = x + x + x ;
definitie van
return res;
d functie
de
f
ti
}
de parameter
aanroep van
public static void main (String[] a)
de functie
{
System out println( driewerf ("Hoera!")
System.out.println(
( Hoera! ) );
}
waarde van de parameter
C
Communicatie
i ti mett ffuncties
ti
 Parameters :
aanroeper geeft
ft waarde
d d
door
aan de methode
 Functie-resultaat
Functie resultaat :
methode geeft waarde
terug aan de aanroeper
met een
return-opdracht
S t
Syntax
van opdracht
d
ht
opdracht
object
.
variabele
=
return
functie
naam
expressie
(
expressie
;
expressie
;
if
(
expressie
)
opdracht
while
(
expressie
)
opdracht
{
opdracht
p
declaratie
)
;
,
else
l
opdracht
d ht
}
O d
Opdrachten
ht
herhalen
h h l
public static void main (String[] a)
{ int x;
x = 1;
while ( x<1000 )
x = 2*x;
}
System.out.println( "kijk:"
kijk: + x );
X
1024
128
512
256
64
32
16
1
8
4
2
1024
zolang de
voorwaarde
geldig is
body wordt
p
steeds opnieuw
uitgevoerd
M
Meer
opdrachten
d
ht
herhalen
h h l
private static int tweeLog
naam ((int
) n)
{
int x, t;
x=1; t=0;
teller telt
n )
while ( x<1000
hoe vaakk er wordt
h
dt
{ x = 2*x;
verdubbeld
t = t+1;
}
accolades smeden
return t;
twee opdrachten
}
tot één body
P bli k
Publieksvraag
Schrijf een functie driewerf
mett een St
String-parameter,
i
t
die 3 herhalingen ervan oplevert
driewerf("Hoera!")
"Hoera!Hoera!Hoera!"
Schrijf
S
h ijf een functie
f
ti veelwerf
l
f
met een String-parameter, en een getal n
die n herhalingen van de String oplevert
V l
Veelwerf-functie
ff
ti
private static String veelwerf (String s, int n)
{
String result;
int t;
t = 0;;
result = "";
while ( t<n )
{ result = result + s ;
t = t+1 ;
}
return result;
}
P bli k
Publieksvraag
Maak een methode macht
mett ttwee parameters
t
grondtal
exponent
(reëel getal)
(natuurlijk getal)
die de waarde oplevert van
grondtal
dt lexponent
M ht
Machtsverhef-functie
h ff
ti
private static double macht (double x, int n)
{
double result;
int t;
t = 0;;
result = 1;
while ( t<n )
{ result = result * x ;
t = t+1 ;
}
return result;
}
V
Vergelijk-operatoren
lijk
t
<
<=
>
>=
==
!=
kleiner dan
kleiner dan of gelijk aan
groter dan
groter dan of gelijk aan
gelijk aan
x=5
x wordt 5 !
ongelijk aan x==5
x 5
is x gelijk aan 5 ?
E
Expressies
i
Expressie met een getal als waarde
2 * (lengte + breedte)
primitief
type int
Expressie met een tekst als waarde
"Hallo " + persoon
object-
type String
E
Expressie
i mett een waarheid
h id als
l waarde
d
teller < exponent
primitief
type boolean
B l
Boolean
expressies
i
Vergelijken van waarden
x <= y
Combineren van andere
boolean expressies
met logische operatoren
&&
||
 !
and
d
or
not
x<0 && y>0
! (x==0 && y==0)
George Boole
(1815-1864)
x!=0 || y!=0
V i b l
Variabelen
aanpassen
x = x*2;
nieuwe waarde
wordt
oude waarde
Afgekorte notaties:
x = x*2;
x *= 2 ;
x = x+5;
x += 5 ;
x = x+1;
x += 1 ;
wordt vermenigvuldigd met
wordt vermeerderd met
wordt opgehoogd
x ++ ;
H h li
Herhaling
mett een tteller
ll
int t ;
t = 0;
for
while
for
( ( t=0
t<x ) ; t<x ; t++ )
{
// doe iets nuttigs
// met t
t ++ ;
}
S t
Syntax
van opdracht
d
ht
opdracht
object
functie
naam
.
variabele
=
return
expressie
(
expressie
;
expressie
;
;
,
else
if
(
expressie
)
opdracht
while
(
expressie
)
opdracht
opdracht
{
)
opdracht
}
declaratie
for
(
expr
;
expr
;
expr
)
opdracht
H h ld h
Herhaalde
herhaling
h li
 Body van een for-opdracht is een opdracht
dat kan zelf ook een for-opdracht
for opdracht zijn!
int x, y;
for (y=0; y<10; y++)
{ for (x=0; x<10;
y x++)
System.out.print( "+" );
System.out.println();
}
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
++++++++++
E t
Extreme
gevallen
ll
Nul keer herhalen
for (y=0; y<0; y++)
System.out.println("hoi");
Oneindig
g vaak herhalen
while (true)
Audio play( "birds
Audio.play(
birds gotta fly"
fly );
System.out.println("hoi");
deze opdracht
komt nooit
aan de beurt!
O b d ld oneindigheid
Onbedoelde
i di h id
x=1;
aantall = 0;
0
while (aantal<10)
x = x*2;
{
aantal = aantal+1;
}
accolades
vergeten...
C
Compiler-meldingen
il
ldi
Foutmeldingen
variabele

a iabele niet gedeclareerd
gedecla ee d
puntkomma vergeten
...
Waarschuwingen
g
deze waarschuwing
is theoretisch
onmogelijk!
unreachable code
statement has no effect
while-statement doesn’t terminate
Het Halting-problem
i onoplosbaar
is
l b
Nietes!
Deze methode
lost het op:
Ha!
En dit dan?
wat komt
er dan uit:
boolean stopt (String filenaam)
{ ....
}
void gemeen (String filenaam)
{ while ( stopt(filenaam)
p(
))
x++;
}
stopt( "Gemeen.java" )
?
Het Halting-problem
stopt( "Gemeen.java" )
i onoplosbaar
is
l b
Twee mogelijkheden:
“G
“Gemeen”
” stopt
t t well
void gemeen (String filenaam)
{ while ( stopt(filenaam) )
xx++;;
}
...dus stopt levert true op
...dus gemeen bijft hangen!
“Gemeen” stopt niet
...dus stopt levert false op
...dus gemeen stopt direct!
dus stopt kan helemaal niet bestaan
tegenspraak!
Hoofdstuk 5
Strings en arrays
F
Functies
ti
en methoden
th d
Eigen functie int k;
k=
kwadraat(5)
Functie uit een library double
d bl d;
d
;
d = Math . sqrt(10)
q ( )
;
Methode:
functie met een object onderhanden
String s, t; s="Hallo";
t=
s . substring(1, 3) ;
Static
methoden
th d
en methoden
th d
Eigen static methode
kwadraat(5)
 Static methode uit een library
geen object
geen object,
maar library-naam
y
Math . sqrt(10)
q ( )
Methode:
functie met een object onderhanden
String-object
String s;
s="Hallo";
s . substring(1, 3)
St i
String-methodes
th d
int
boolean
String
String
String
String
String
length
equals
concat
substring
substring
toUpperCase
toLowerCase
()
(String s)
(String s)
(int start)
(int start, int eind)
()
()
concatt en
substring
b t i
s
String s, t, u, v, w;
s = "ham";
t = "burger";
burger ;
ham
u = s.concat(t);
s+t;
v = u.substring(3);
t
u
v
burger
hamburger
burger
 = u.substring(3,
w
b t i (3 7);
7)
““van en
met”
““tot en
zonder”
w
burg
012345678
hamburger
L
Losse
letters
l tt
String
substring
(int begin, int eind)
String voorletter;
voorletter = s . substring(0
substring(0,1);
1);
 h
char
charAt
h At
char eerste;
eerste = s . charAt(0);
(i t positie)
(int
iti )
P i iti
Primitieve
ttypes
int
gehele
h l getallen
t ll
-17,
17 -5,
5 0,
0 3,
3 178
double
reëele getallen
3.141, 2.0, -1.5E8
boolean
waarheidswaarden false, true
char
losse symbolen ’A’,
A , ’B’,
B , ’Z’,
Z , ’a’,
a , ’4’,
4 , ’#’,
# , ’:’
:
P bli k
Publieksvraag
// schrijf een static methode die telt hoe
// vaak een symbool voorkomt in een String
// voorbeeld-aanroep:
int n;
n = freq(’e’,
f (’ ’ ”some
”
text”” ));
// hint: gebruik een for opdracht
T l symbool-frequentie
Tel
b lf
ti
private static int freq(char x, String s)
{
int aantal;;
aantal = 0;
int t;
for (t=0; t<s.length(); t++)
charAt(t)==x )
if ( ss.charAt(t)==x
aantal ++ ;
return aantal;
}
St i
String
versus char
h
 String
 klasse
 object-verwijzing
 nul,
nul een of meer…
meer
 ""
"A"
"hello"
 methoden
equals
concat
substring
char
primitief type
directe waarde
precies één symbool
’A’
operatoren
==
<
+
Arrays
Array: rij genummerde variabelen
declaratie van
een arrayy
int [ ] tabel;
tabel = new int [5];
tabel
5
length
0
1
2
3
4
creëren van
het eigenlijke
array-object
G b ik van een array
Gebruik
’t zijn echte variabelen:
tabel [[2]] = 37;;
tabel
x = tabel [2] + 5;
if (tabel.length<10) ...
x
5
length
0
42
1
37
2
3
tabel.length = 10;
echter de lengte
mag je niet wijzigen
4
G b ik van een array
Gebruik
variabele als index in de array
tabel
tabel
tabel
tabel
tabel
[0]
[1]
[2]
[3]
[4]
=
=
=
=
=
0;
0;
0;
0;
0;
for (t=0; t<5; t++)
tabel [t] = 0;
tabel
5
length
0
0
0
1
0
2
0
3
0
4
A
Array
als
l parameter
t
int totaal ( int [ ] tabel )
{
int resultaat; int t;
resultaat = 0 ;
for (t=0; t<tabel.length; t++)
resultaat +=
+ tabel [t] ;
}
return resultaat;
tabel
5
length
12
0
95
1
11
2
23
3
15
4
A
Array
als
l parameter
t
int kleinste ( int [ ] tabel )
{
int resultaat; int t;
resultaat = tabel [[0]] ;
for (t=0; t<tabel.length; t++)
if (tabel [t] < resultaat)
resultaat = tabel [t];
}
return resultaat;
tabel
5
length
12
0
95
1
11
2
23
3
15
4
T l symbool-frequentie
Tel
b lf
ti
private static int
{
int aantal;;
aantal = 0;
freq (char x, String s)
int t; char c;
for (t=0; t<s.length(); t++)
c = s.charAt(t);
()
{
if (c==x)
aantal ++ ;
}
return
t
aantal;
t l
}
Turf de frequentie
van elke
lk letter
l tt
voidfreq
frequentie
( String s)
private static int
(char x,
{
int aantal;
;
[ ] aantal;
aantal = 0;
new int [128];
int t; char c;
for (t=0; t<s.length(); t++)
c = s.charAt(t);
()
{
if (c==x)
( c>='a' && c<='z' )
aantal ++
;
[c] ++;
}
for ( c='a' ; c<='z' ; c++ )
return
t System.out.println(
t l
S aantal;
l ( c + ":
" " + aantal[c]
l[ ] );
)
}
Methode met
een array als
l resultaat
lt t
int []freq
frequentie
( String s)
private static int
(char x,
{
int aantal;
;
[ ] aantal;
aantal = 0;
new int [128];
int t; char c;
for (t=0; t<s.length(); t++)
c = s.charAt(t);
()
{
if (c==x)
( c>='a' && c<='z' )
aantal ++
;
[c] ++;
}
return
t
aantal;
t l
}
Prakticumopgave
pg
2
Turing machines
Het Halting-problem
i onoplosbaar
is
l b
Nietes!
Deze methode
lost het op:
Ha!
En dit dan?
wat komt
er dan uit:
boolean stopt (String filenaam)
{ ....
}
void gemeen (String filenaam)
{ while ( stopt(filenaam)
p(
))
x++;
}
stopt( "Gemeen.java" )
?
Al
Alan
T
Turing
i
(1912
(1912-1954)
1954)
1936:
"O computable
"On
t bl numbers,
b
with an application to the
Entscheidungsproblem "
Al
Alan
T
Turing
i
(1912
(1912-1954)
1954)
en ik ::-))
Al
Alan
T
Turing
i
(1912
(1912-1954)
1954)
1936 O
1936:
On computable
t bl numbers
b
 Turing machine
1943: Enigma crack
1946: eerste
Engelse
computer
1950: Computing
p
g machineryy and intelligence
g
 Turing test
"can machines think?"
Wi k di
Wiskundige
logica
l i
(1910) Russell Principia Mathematica:
waarheid
h id en bewijsbaarheid
b ij b h id
(1931)
(
) Gödel incompleteness
p
-stelling:
g
“sommige waarheden zijn niet bewijsbaar”
(1900) Hilbert 30 open vragen,
vragen o.a.:
oa:
“kun je van elke uitspraak beslissen,
of hij waar is of niet?”
((Entscheidungsproblem)
g p
)
52
T i
Turing
M
Machine:
hi
id
idee
 Tape met symbolen
 Machine
M hi mett toestand
t
t d
 Transitie-regels
 Startconfiguratie
 Machine stopt als
geen regels
toepasbaar
 Machine
M hi kan
k o.a. echt
ht
rekenen!
http://math.hws.edu/TMCM/java/labs/xTuringMachineLab.ht
ml
53
B
Berekenbare
k b
getallen
t ll
 Berekenbaar getal:
output van een Turing
Turing-machine
machine
 De Turing-machines zijn aftelbaar
( alfabetische
(op
lf b ti h volgorde
l d van regels-tekst)
l t k t)
 Sommige Turing-machines geven geen output
( d td
(omdat
de berekening
b k i niet
i t eindigt)
i di t)
 Halting-probleem:
“eindigt
d de
d berekening
b k
van
Turing-machine met nummer M ?”
54