Uitwerkingen Mulo-A Examen 1923 Meetkunde Algemeen

Uitwerkingen Mulo-A Examen 1927 Meetkunde Algemeen
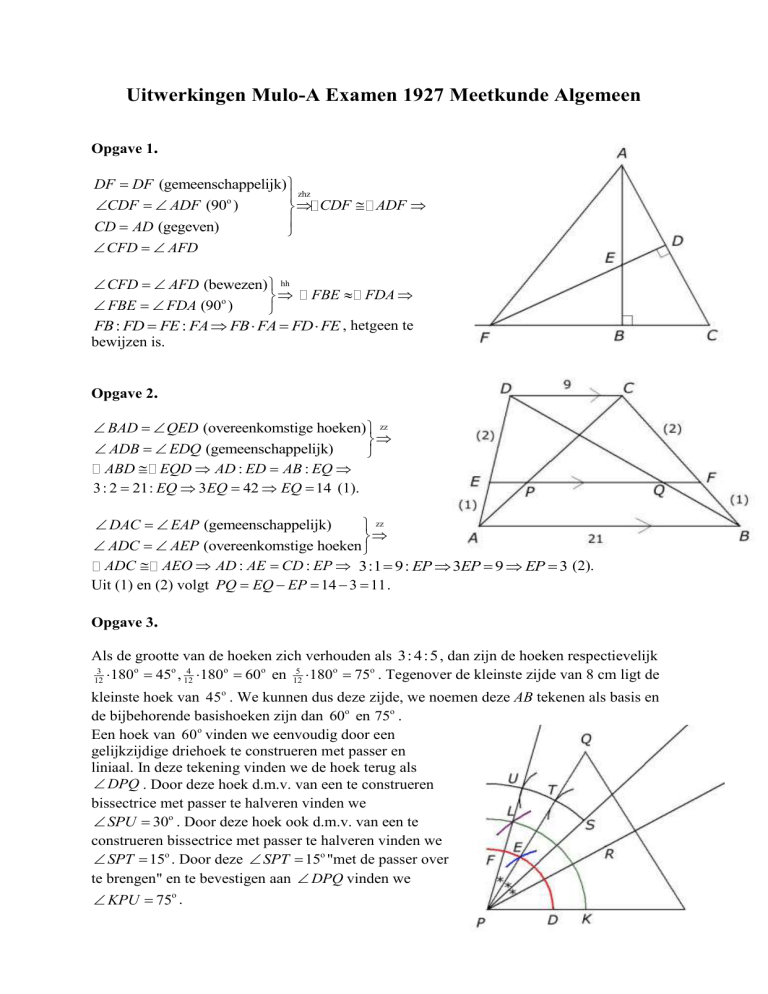
Opgave 1.
DF  DF (gemeenschappelijk) 
 zhz
CDF   ADF (90o )
  CDF  ADF 

CD  AD (gegeven)

 CFD   AFD
 CFD   AFD (bewezen)  hh
  FBE  FDA 
 FBE   FDA (90o )

FB : FD  FE : FA  FB  FA  FD  FE , hetgeen te
bewijzen is.
Opgave 2.
 BAD   QED (overeenkomstige hoeken)  zz

 ADB   EDQ (gemeenschappelijk)

ABD  EQD  AD : ED  AB : EQ 
3 : 2  21: EQ  3EQ  42  EQ  14 (1).
 DAC   EAP (gemeenschappelijk)
 zz

 ADC   AEP (overeenkomstige hoeken 
ADC  AEO  AD : AE  CD : EP  3:1  9: EP  3EP  9  EP  3 (2).
Uit (1) en (2) volgt PQ  EQ  EP  14  3  11 .
Opgave 3.
Als de grootte van de hoeken zich verhouden als 3: 4: 5 , dan zijn de hoeken respectievelijk
o
o 4
o
o
o
o
3
5
12 180  45 , 12 180  60 en 12 180  75 . Tegenover de kleinste zijde van 8 cm ligt de
kleinste hoek van 45o . We kunnen dus deze zijde, we noemen deze AB tekenen als basis en
de bijbehorende basishoeken zijn dan 60o en 75o .
Een hoek van 60 o vinden we eenvoudig door een
gelijkzijdige driehoek te construeren met passer en
liniaal. In deze tekening vinden we de hoek terug als
 DPQ . Door deze hoek d.m.v. van een te construeren
bissectrice met passer te halveren vinden we
 SPU  30o . Door deze hoek ook d.m.v. van een te
construeren bissectrice met passer te halveren vinden we
 SPT  15o . Door deze  SPT  15o "met de passer over
te brengen" en te bevestigen aan  DPQ vinden we
 KPU  75o .
De constructie kan als volgt verlopen: teken
lijnstuk AB (8 cm). Breng hoek A over door
vanuit de hulptekening de rode boog DEF
over te brengen naar punt A op AB en de
afstand DE (blauw boogje) af te passen bij
hoek A. Op dezelfde wijze brengen we hoek
B over. Verleng AE en BL tot hun snijpunt C.