Voorbeeld examen 2

Voorbeeld examen 1
Vraag 1 (5 punten):
Bespreek zo volledig mogelijk de binomiaal verdeling
(definitie, kansverdeling met uitleg, grafische voorstelling, verwachtingswaarde en variantie, verband
met andere verdelingen, toepassingen, steekproefverdeling…)
Vraag 2 (4 punten):
a) Definieer de begrippen covariantie en correlatie voor twee continue toevallige variabelen X en Y,
en leg kort uit waarvoor je deze begrippen gebruikt.
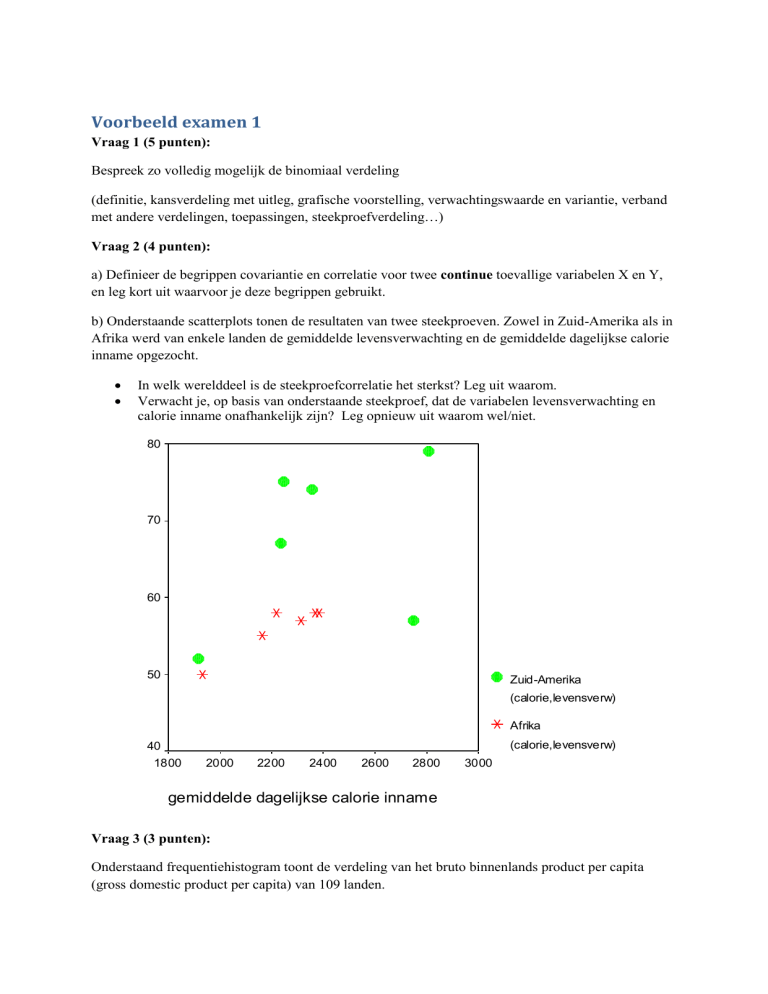
b) Onderstaande scatterplots tonen de resultaten van twee steekproeven. Zowel in Zuid-Amerika als in
Afrika werd van enkele landen de gemiddelde levensverwachting en de gemiddelde dagelijkse calorie
inname opgezocht.


In welk werelddeel is de steekproefcorrelatie het sterkst? Leg uit waarom.
Verwacht je, op basis van onderstaande steekproef, dat de variabelen levensverwachting en
calorie inname onafhankelijk zijn? Leg opnieuw uit waarom wel/niet.
80
70
60
50
Zuid-Amerika
(calorie,levensverw)
Afrika
(calorie,levensverw)
40
1800
2000
2200
2400
2600
2800
3000
gemiddelde dagelijkse calorie inname
Vraag 3 (3 punten):
Onderstaand frequentiehistogram toont de verdeling van het bruto binnenlands product per capita
(gross domestic product per capita) van 109 landen.
a) Welke maatstaven kan je gebruiken om de ligging van het bbp/capita te bestuderen?
b) Welke maatstaf voor ligging lijkt jou het meest aangewezen in deze concrete situatie? Leg uit
waarom.
c) Welke andere grafische voorstellingen kan je gebruiken om de ligging voor te stellen?
Histogram
30
20
Std. Dev = 6479,84
Mean = 5860,0
N = 109,00
0
0
0,
0
0,
00
22 ,0
0
00
20 ,0
0
00
18 ,0
0
00
16 ,0
0
00
14 ,0
0
00
12 ,0
0
00
10
,0
00
80
,0
00
60 0
,
00
40
,0
00
20
Frequency
10
Gross domestic product / capita
Descriptives
Gross domestic
product / capita
Mean
95% Confidence
Interval for Mean
5% Trimmed Mean
Median
Variance
Std. Deviation
Minimum
Maximum
Range
Interquartile Range
Skewness
Kurtos is
Lower Bound
Upper Bound
Statistic
5859,98
4629,73
Std. Error
620,66
7090,23
5349,74
2995,00
4,2E+07
6479,84
122
23474
23352
6674,50
1,146
-,028
,231
,459
Vraag 4 (4 punten):
Een verzekeringsmaatschappij geeft voor de opslagplaats van een bepaalde kunsthandel een brandpolis
uit ter waarde van 85000 EUR en met een looptijd van 1 jaar. Uit ervaring weet men dat de kans dat
in dit welbepaalde jaar een brand alle goederen in deze opslagruimte verwoest 0.1% is, de kans dat er
voor 50% schade aangebracht wordt 1% is, terwijl de kans dat er voor 25% schade is, 3% bedraagt.
Veronderstel tenslotte dat er naast deze drie schadegevallen geen andere schadegevallen mogelijk zijn.
Bovendien zal de verzekeringsmaatschappij nooit een volledige vergoeding uitbetalen voor de
beschadigde goederen: de klant betaalt steeds de eerste schijf van 2500 EUR (onafhankelijk van de
grootte van de schadeclaim).
a) Geef de kansverdeling van het bedrag dat de verzekeringsmaatschappij zal uitbetalen aan de
kunsthandelaar.
b) Welk bedrag moet de verzekeringsmaatschappij voor dergelijke polissen (met zelfde bedrag,
looptijd, risico’s) vragen om gemiddeld een break-even resultaat te halen op deze polissen (dus geen
winst, geen verlies).
Vraag 5 (4 punten):
Een firma die medische apparatuur produceert brengt een nieuw type sonde op de markt, ontwikkeld
voor kijkoperaties. Deze sonde bevat een zeer gevoelige vitale elektronische component waarvan de
gemiddelde levensduur slechts 15 minuten is.
a) Als je weet dat een gemiddelde kijkoperatie waarvoor dit toestel ontwikkeld is 20 minuten duurt, is
het gebruik van dergelijke sonde dan zinvol? Hou enkel rekening met de levensduur en niet met
economische of medische overwegingen om de sonde wel/niet te gebruiken.
b) Zou je dergelijke sonde kopen als je weet dat er niet 1, maar 2 dergelijke componenten inzitten, die
beide onafhankelijk van mekaar werken?
Voorbeeld examen 2
Vraag 1 (5 punten):
Bespreek zo volledig mogelijk volgende items voor de exponentiële verdeling (maar zonder
bewijzen):
definitie, veronderstellingen, dichtheidsfunctie, grafiek van de dichtheidsfucntie, verwachtingswaarde
en variantie, geheugenloosheid, verband met andere verdelingen, veralgemening, zinnige
toepassingen.
Vraag 2 (3 punten):
Bespreek zo volledig mogelijk (maar zonder bewijzen) de verdeling van het steekproefgemiddelde X
in geval van grote steekproeven uit een niet normaal verdeelde populatie: overloop de belangrijkste
eigenschappen van de toevallige variabele X (met uitleg en tekeningen) en geef een zinnige
toepassing.
Vraag 3 (4 punten):
In een socio-economische enquête, afgenomen bij 2654 personen, werd o.a. gepeild naar een aantal
persoonlijkheidskenmerken van de Vlaming.
Eén van de uitspraken die tot de enquête behoorde, is
« Streven naar persoonlijk succes is belangrijker
dan een goede relatie met je naaste »
(verder afgekort als “persoonlijk succes is belangrijker”).
De ondervraagde moest zijn mening over deze uitspraak weergeven door middel van een ordinale
vijfpuntenschaal, waarbij
1 = volledig mee eens
2 = mee eens
3 = neutraal
4 = niet mee eens
5 = helemaal niet mee eens
In een eerste fase van het onderzoek vraagt men zich af of mannen anders dan vrouwen oordelen over
deze uitspraak. De resultaten van de enquête werden afzonderlijk voor mannen en vrouwen verwerkt
in SPSS. Hieronder vind je een aantal beschrijvende datastatistieken en een aantal grafische
voorstellingen
Gevraagd: Hebben, in onderstaande steekproef, mannen duidelijk een andere houding dan vrouwen
t.o.v. het streven naar persoonlijk succes? Zo ja, leg uit in welk opzicht er (duidelijke) verschillen zijn
en leg uit waarop je uw conclusie baseert. Oordeel eerst zelf of alle geleverde berekeningen/grafieken
zinvol zijn of niet (en dus al of niet mogen gebruikt worden). Bespreek zowel ligging, spreiding als
scheefheid.
Histogram
For GESLACHT= man
800
600
Frequency
400
200
Std. Dev = ,98
Mean = 3,7
N = 1352,00
0
1,0
2,0
3,0
4,0
persoonlijk succes is belangrijker
5,0
Histogram
For GESLACHT= vrouw
800
600
Frequency
400
200
Std. Dev = ,96
Mean = 3,8
N = 1302,00
0
1,0
2,0
3,0
4,0
5,0
persoonlijk succes is belangrijker
6
5
4
3
2
1
0
N=
GESLACHT
1352
1302
man
vrouw
Descriptives
persoonlijk succes
is belangrijker
GESLACHT
man
Mean
Median
Variance
Std. Deviation
Minimum
Maximum
Range
Interquartile Range
Skewness
Kurtos is
Mean
Median
Variance
Std. Deviation
Minimum
Maximum
Range
Interquartile Range
Skewness
Kurtos is
vrouw
Statistic
3,6916
4,0000
,961
,9803
1,00
5,00
4,00
1,0000
-,891
,488
3,8410
4,0000
,926
,9620
1,00
5,00
4,00
,0000
-1,115
1,130
Vraag 4 (4 punten):
Een pompstation stelt vast dat het verkoopspercentage van hun loodvrije benzine super95 ( = X ) en
super98 ( = Y ) beschreven kan worden door de dichtheidsfunctie
f X ,Y x, y   9x 2 y 2 met
0  x 1
0  y 1
.
a) Bewijs dat bovenstaande functie inderdaad een dichtheidsfunctie is.
b) Wat is de kans dat meer dan 75% van super98 en minder dan 25% van super95 verkocht wordt?
c) Zijn super95- en super98- verkoopscijfers onafhankelijk van elkaar?
Vraag 5 (4 punten):
Een vensterraam producerend bedrijf Vesco bestelt gewalste aluminium-platen met een dikte van
0.2mm. De kans dat een plaat niet voldoet aan de gestelde voorwaarden is 10%. De platen worden
verkocht in pakketten van 10 platen. Vesco zal een pakket terugsturen wanneer minstens 2 platen niet
voldoen aan hun voorwaarden.
a) Bereken de kans dat een pakket wordt teruggestuurd.
b) Als het bedrijf Vesco nu 100 pakketten bestelt, hoeveel slechte pakketten zouden er dan
gemiddeld genomen teruggestuurd worden?
c) Veronderstel nu dat de platen worden verkocht in pakketten van 20 platen. Hoeveel slechte platen
mogen er maximaal in zo’n pakket zitten, wil de kans dat het pakket wordt teruggestuurd kleiner
zijn dan de kans dat een pakket met 10 platen wordt teruggestuurd.
Voorbeeld examen 3
Theorie:
MEERKEUZEVRAGEN
1) Van een reeks waarnemingen wordt een boxplot geconstrueerd. Hoeveel procent van deze
waarnemingen heeft een warde die groter is dan de bovenrand van de doos in de boxplot?
A: 15%
B: 25% x
C: 50%
D: 75%
2) Voor de steekproef met waarneming (6,4) en 7,1) bedraagt de Pearson correlatiecoëfficiënt tussen
de geobserveerde variabelen X en Y
A: 1
B:-1 x
C: -0,5
D:0,5
3) Vraag met een BMW:
Verkochte eenheden: 40
50
60
Kans:
0,3
0,2
0,5
Wat is de variantie van het aantal verkochte eenheden?
A: 45
B: 76 x
C: 1234
D: 3456
4) Voor een steekproef met waarnemingen (75, 70), (80, 77)en (76, 67) bedraagt de Spearman
rangcorrelatiecoëffieciënt tussen de geobserveerde variabelen X en Y
A: 1
B:-1
C: -0,5 x
D:0,5
5) De hoeveelheid reiskoffers op een passagiersvliegtuig heeft een gemiddelde van 200 en een
standaardafwijking van 220. De kans dat de gemiddelde hoeveelheid reiskoffers van een lukraak
samengestelde groep van 100 vliegtuigen minstens 250 reiskoffers bedraagt is
A: 0,5673
B: 0,0116 x
C: 0,8334
D: 0,0236
6) De eerste Fries Elfsteden vond plaats op 5 januari 1909. In januari 1997 werd de 15de en voorlopig
laatste Elfstedentocht. Gemiddeld betekent dit dat de schaatstocht om de
..103... / 15 ≈ ..6,87.. jaar plaats vindt. Ga ervan uit dat het aantal Elfstedentochten per jaar Poisson
verdeeld is. Wat is de kans dat er de volgende 5 jaar geen Elfstedentocht zal plaatsvinden?
A: 0,07
B: 0,48 x
C: 0,83
D: 0,02
7) Vraag ivm bekendste Belgische statisticus -> Adolphe Quetelet
8) Lange maar makkelijke vraag waarbij je gwn 1/6! moest doen.
9) Vraag met variantie berekenen
10) Een student beweert dat de covariantie tussen twee kansvariabelen X en Y gelijk is E(XY), is dit
waar?
A: Neen dat is nooit waar.
B: Ja, indien E(X)=0 en E(Y)=0 x
C: Ja, dit is altijd waar.
D: Ja, indien X en Y onafhankelijk kansvariabelen zijn.
Grote vragen:
-Een kansvariabele X is beta verdeeld met parameters 𝛼 en 𝛽. De kansdichtheid van een beta
verdeelde kansvariabele X is gelijk aan: 𝑓(𝑥) =
Γ(𝛼+ 𝛽)
Γ(𝛼)Γ(𝛽)
𝑥 𝛼−1 (1 − 𝑥)𝛽−1
In deze uitdrukking is 0 ≤ x ≤ 1, stelt Γ() de gamma fucntie voor, en zijn Γ(𝛼), Γ(𝛽) en Γ(𝛼 + 𝛽)
constanten. De verwachte waarde en de variantie van een beta verdeelde kansvariabele zijn gelijk aan:
𝛼
𝛼𝛽
𝜇𝑥 = 𝐸(𝑋) = 𝛼+ 𝛽 en 𝜎𝑥2 = var(X) = (𝛼+ 𝛽)2 (𝛼+ 𝛽+1)
Wat is de kansdichtheid van Y = 1- X ? Hoe heet deze en wat zijn de parameters ervan? Wat is de
verwachte waarde van Y? Wat is de variantie van Y?
Oplossing:
Via transformatiestelling oplossen!
° y = g(x) = 1-n : Strikt dalend, dus ok
° 𝑔−1 (y) = n = 1-y
°|
𝑔−1 (𝑦)
|
𝑑𝑦
= |−1|
° 𝑓𝑦 (𝑦) =
Γ(𝛼+ 𝛽)
Γ(𝛼)Γ(𝛽)
(1 − 𝑦)𝛼−1 (1 − 1 + 𝑦)𝛽−1
=
...
𝑦 𝛽−1
(1 − 𝑦)𝛼−1
y~Beta verdeeld met parameters 𝛽 𝑒𝑛 𝛼
𝛽
E(y) = 𝛼+ 𝛽
𝛼𝛽
Var(y) = (𝛼+ 𝛽)2 (𝛼+ 𝛽+1)
OEFENINGEN :
-Oefening uit ‘Kansen en verwachtingen’ van de duivenmelker, met X= reistijd snelste duif etc.
-Kansboom opstellen en tekenen
-Goed het verschil tussen ratio/interval/kwalitatief/kwantitatief geschaald kennen.