Voorkennis H2 Uitleg

Voorkennis: Kwadratische vergelijking oplossen
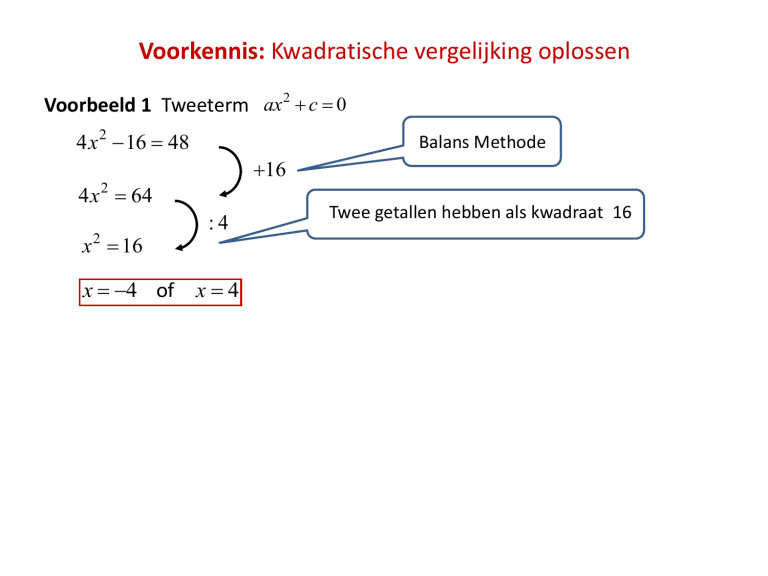
Voorbeeld 1 Tweeterm ax 2  c  0
4 x 2  16  48
Balans Methode
16
4 x 2  64
x 2  16
x  4 of
:4
x4
Twee getallen hebben als kwadraat 16
Voorkennis: Kwadratische vergelijking oplossen
Voorbeeld 2 Tweeterm ax 2  bx  0
2 x2  6 x  0
x buiten haakjes halen
x(2 x  6)  0
Als AB  0 dan moet gelden A  0 of B  0
x  0 of 2 x  6  0
6
x  0 of 2 x  6
x  0 of
x3
:2
balans methode
Voorkennis: Kwadratische vergelijking oplossen
Voorbeeld 3 Drieterm ax2  bx  c  0 ontbindbaar
Op 0 herleiden.
2 x 2  24  14 x
 14 x
2 x 2  14 x  24  0
:2
x  7 x  12  0
2
2
Zorg dat er voor de x een 1 staat
Zoek twee getallen met product 12
en met som 7
3  4  12
 3  4  7
( x  3)( x  4)  0
x  3  0 of
x  3 of
x4 0
x4
Als AB  0 dan moet gelden A  0 of B  0
Voorkennis: Kwadratische vergelijking oplossen
Voorbeeld 4
(2 x  8)( x  2)  0
2x  8  0
2 x  8
x  4
Deze staat al in de vorm A  B  0 !!!!!!
Als AB  0 dan moet gelden A  0 of B  0
x20
of
8
of
x2
:2
of x  2
2
Voorkennis: Kwadratische vergelijking oplossen
Voorbeeld 5
Rechts staat géén 0 !!!!!
( x  1)( x  5)  3
Haakjes wegwerken
x 2  5 x  x  5  3
3
x  6x  8  0
2
( x  2)( x  4)  0
x  2  0 of
x  2 of
x40
x4
Zoek twee getallen met product 8
en met som 6
2  4  8
 2  4  6
Als AB  0 dan moet gelden A  0 of B  0