lic-les-06 breking vanuit stof

Breking
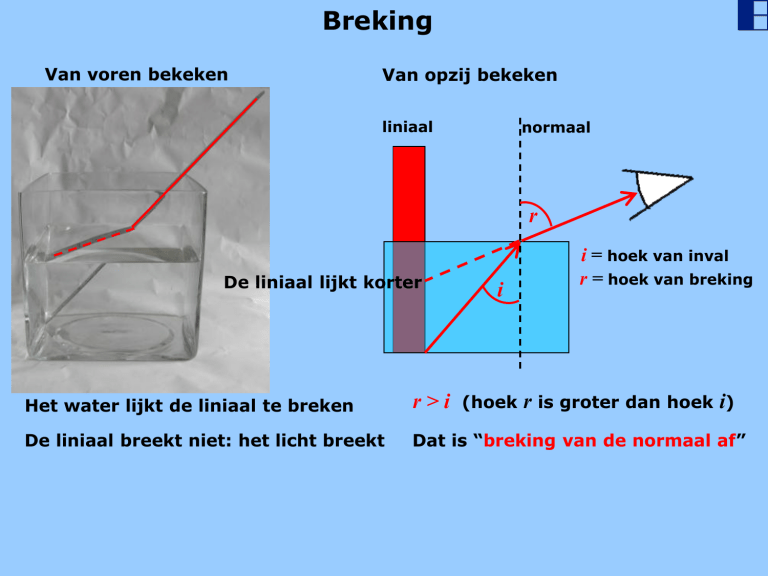
Van voren bekeken
Van opzij bekeken
liniaal
normaal
r
De liniaal lijkt korter
i
(hoek
i = hoek van inval
r = hoek van breking
r is groter dan hoek i)
Het water lijkt de liniaal te breken
r>i
De liniaal breekt niet: het licht breekt
Dat is “breking van de normaal af”
Wet van Snellius
• Een lichtstraal, die vanuit water
• Naar lucht gaat
• Breekt volgens de Wet van Snellius:
• n heet de brekingsindex
• Elke stof heeft een andere
ni  sin i  nr  sin r
r
n
nlucht  1,00 nwater  1,33 nglas  1,53
Lucht
grensvlak 
Water
• Voorbeeld (waterlucht):
i = hoek van inval in het water
ni = brekingsindex van water (= 1,33)
r = hoek van breking in de lucht
nr = brekingsindex van lucht (= 1,00)
i
• 4 grootheden. Hoe maak je de 4 formules?
1.
ni  sin i  nr  sin r
4  6  3 8 (de tip van Flip)
nr  sin r
nr  sin r
ni 
2. sin i 
ni
sin i
4
38
6
6
38
4
 normaal
ni  sin i
n

3. r
sin r
3
46
8
ni  sin i
4. sin r 
nr
8
46
3
Breking van water  lucht
•
•
•
•
Een lichtstraal, die vanuit water
Naar lucht gaat
Breekt volgens de Wet van Snellius:
Brekingsindex
ni  sin i  nr  sin r
nlucht  1,00 nwater  1,33
• Voorbeeld:
r = ?o
Lucht
grensvlak 
r?
nr  1,00
Rekenmachine: MODE MODE 1
i  400
ni  1,33
ni  sin i 1,33  sin 40o
sin r 
 0,85...

nr
1,00
1
r  sin 0,85...  58,...o
r  59o
o
Water
i = 40o
 Normaal
Rekenmachine: SHIFT sin =
Breking van waterlucht: breking van de normaal af