PDF-slides Planeetbeweging

Afstanden tot planeten
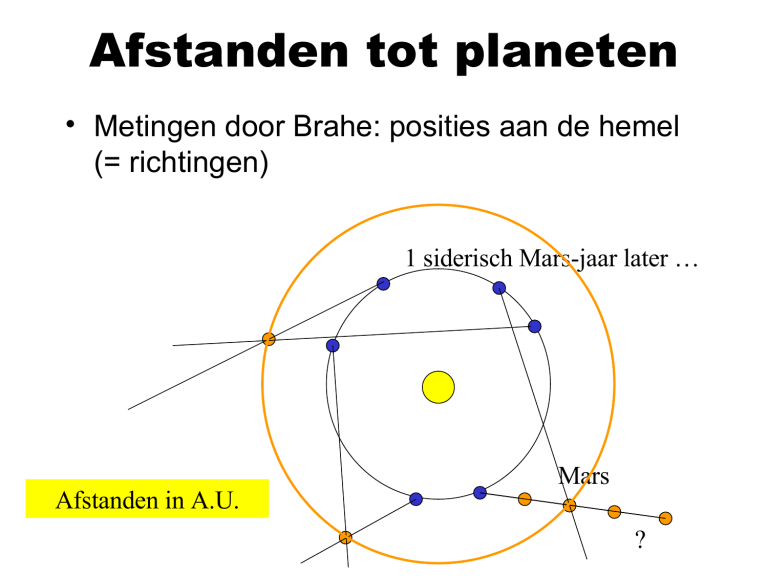
• Metingen door Brahe: posities aan de hemel
(= richtingen)
1 siderisch Mars-jaar later …
Afstanden in A.U.
Mars
?
Banen van planeten
De wetten van Kepler (afgeleid met behulp van de
metingen van Brahe):
1. Ellipsvormige banen, Zon in brandpunt
2. De lijn Zon-planeet dekt in gelijke tijden gelijke
oppervlaktes af (perkenwet)
3. (omlooptijd)2 is evenredig aan (gemiddelde straal)3
snel
traag
De ellips
• Cirkel: afstand tot centrum is constant
• Ellips: som van afstanden tot twee brandpunten is
constant, = L
Vgl. in poolcoordinaten
rond een brandpunt:
r
θ
F
‘semi-latus rectum’ l
excentriciteit e
Newtons gravitatiewet
dA
• Kepler 2 ) kracht is centraal
r
dt v?
– (constant impulsmoment ( centrale kracht)
• Stel
rv? ´ r2(dθ/dt)=h
Newtons gravitatiewet
Baan onder centrale acceleratie a(r), met impulsmoment h=r2dθ/dt:
dus
Newtons gravitatiewet
• Baan onder centrale acceleratie a(r):
• Een ellips in poolcoordinaten heeft als
vergelijking (l, e, θ0 const.)
excentriciteit:
e=0 cirkel
e<1 ellips
• Dus de acceleratie van planeet is
e=1 parabool
e>1 hyperbool
Newtons gravitatiewet
3e wet van Kepler: straal3 = K £ Periode2
Benadering: baan ' cirkel, straal=a
2
l = a; h = a (dθ/dt)
dθ/dt = 2π / Periode
Planeet voelt acceleratie
2
2
3
2
(h2/l) /r2 = (2π a /P) /a = 4π K /a2
2
Elke planeet voelt acceleratie 4π K/r2, zelfde K
Universele wet van de zwaartekracht
Newtons gravitatiewet
• Kracht = massa £ acceleratie (Newton II)
• Dus de Zon oefent een kracht 4π2 K m/r2 uit op een
planeet met massa m
• Actie = reactie, dus de planeet oefent dezelfde kracht
uit op de Zon (Newton III)
• Kracht is dus / m × mzon
F = G m1 m2 / r2
Gravitatieconstante = 6.67× 10-11 kg-1 m3 s-2
oppervlaktezwaartekracht
• Aan aardoppervlak:
acceleratie g = 9.8m/s2 = G MA / rA2
rA = 6400km
dus MA=g rA2/G = 6×1024 kg
• Bij gelijke dichtheid schaalt g met r
– Bijv.: de Maan heeft r~0.25 rA, dus g~1/4 aardse waarde
(1/6 in werkelijkheid – de dichtheid van de Maan is lager)
• Ontsnappingssnelheid (2GM/r)1/2 =(2gr)1/2
– schaalt ook met r bij gelijke dichtheid
Getijdewerking:
limiet van Roche,
stabiliteitslimiet
R
planeet
M
r
GM/(R-d)2
maan
d
m
GM/R2
GM/(R+d)2
Getijden >
oppervlaktezwaartekracht van
maan ⇒ maan valt
uiteen
Ringvorming!
NB betere analyse: 21/3 → 2.44
Venus-overgang
• Hoe groot is de Astronomische eenheid?
• Manier om uit een afstand op Aarde te relateren en
een gemeten hoek de afstand tot Venus te bepalen.
Aarde
E
Venus
Zon
G
0.28 A.U.
0.72 A.U.
γ
Afstand D
Tijdsduren overgangen EF en GH ⇒ hoek γ
• 1A.U.=D / tan γ / 0.28 = 149.6 miljoen km
F
H
Venus Transit
• Juni 2004
– weer in jun 2012,
dec 2117, dec
2125
– Waarom steeds in
juni of december?
Fysisch eigenschappen
van de zon
• Aardbaan: P=1 jaar, a=1 A.U.
• Zon heeft hoekdiameter 30’=900”
• Mzon = 4π2 (A.U.)3 / (1 jaar)2 / G
= 4π2 (1.49£1011m)3 / (3.1£107 s)2 / 6.67£10-11
= 2£1030kg
• Rzon = 900”/206235£(A.U.) = 6.6£108m
• Dichtheid 1660 kg/m3
Exoplaneten
kleine, snelle banen
• Planeten rond andere sterren
– >200 gevonden, incl 3-planetenstelsels!
– Nu: indirecte meting via de baanbeweging
van de ster:
• sterbaan met straal m/M x planeetbaanstraal
• sternelheid m/M x baansnelheid planeet
• Voorbeeld: Jupiter in Aardbaan:
m/M=1/1000
v=30km/s ⇒ 30 m/s
– Toekomst: astrometrie: directe meting
van de baanbeweging van de ster
Grote, trage banen