Kijklijnen en kijkhoeken Richting en koers

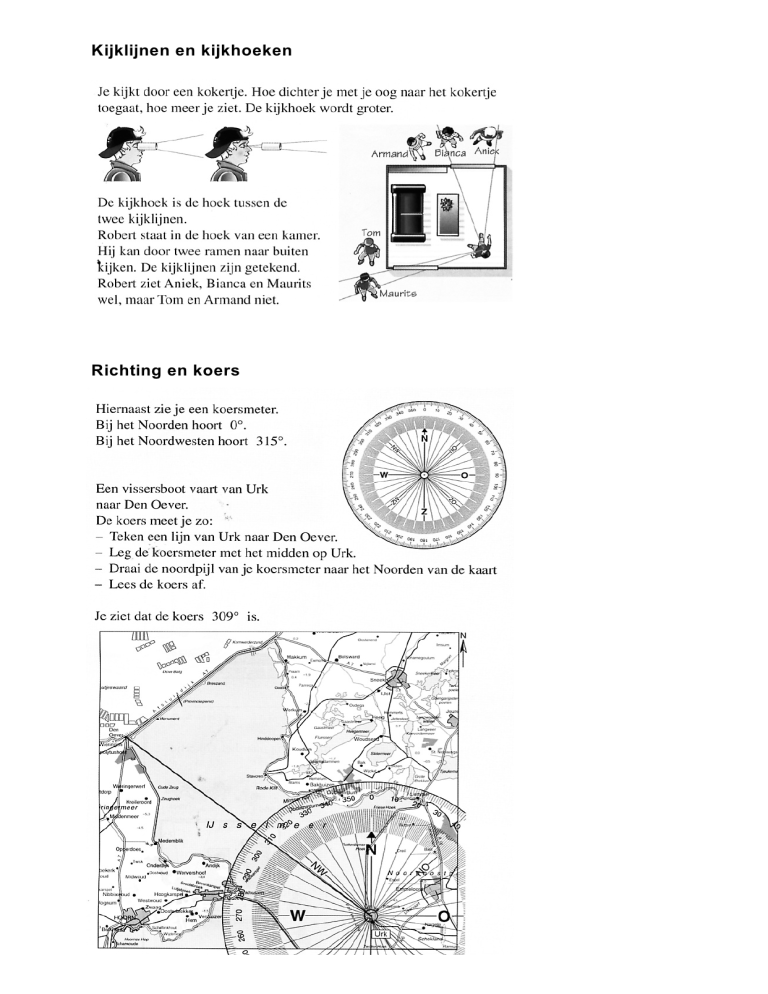
Kijklijnen en kijkhoeken
Richting en koers
Schaal en afstand
Aanzichten
Hoeken meten
Hoeken tekenen
Driehoeken tekenen
Lijnsymetrie
Sommige vormen kun je dubbelvouwen, zodat de twee helften precies op elkaar
passen. De figuur heet dan vouwsymetrisch of lijnsymetrisch. De vouwlijn is de
symetrie-as (spiegel-as). Soms zijn er meerder symetrie-assen (denk bijvoorbeeld
aan vierkant, cirkel of gelijkzijdige driehoek)
Schuifsymetrie, vlakvulling
Hoeken berekenen
Hoeken berekenen in een driehoek
Namen en eigenschappen van vlakke figuren
Oppervlakte en omtrek
naam
oppervlakte
omtrek
vierkant
zijde x zijde
alle zijden optellen
rechthoek
lengte x breedte
alle zijden optellen
driehoek
opp. rechthoek die je eromheen
kunt tekenen gedeeld door 2
alle zijden optellen
cirkel
ð x straal x straal
ð x diameter
In plaats van ð mag je ook 3,14 nemen
Stelling van Pythagoras (werkt alleen in een rechthoekige driehoek!)
X2
%X
Ruimtefiguren
Uitslagen (bouwplaten)
Door middel van de uitslag kun je de oppervlakte van een ruimtefiguur berekenen.
De uitslag bestaat immers uit vlakke figuren!
Inhoud
Ieder ruimtefiguur heeft een inhoud. Algemeen kun je zeggen:
inhoud ruimtefiguur = oppervlakte grondvlak x hoogte
ruimtefiguur
vorm grondvlak
oppervlakte grondvlak
inhoud
kubus
vierkant
zijde x zijde
zijde x zijde x hoogte
balk
rechthoek
lengte x breedte
lengte x breedte x hoogte
prisma
driehoek
lengte x breedte : 2
lengte x breedte: 2 x hoogte
cilinder
cirkel
ð x straal x straal
ð x straal x straal x hoogte