Mechanica van Materialen

Mechanica van Materialen: Voorbeeldoefeningen uit de cursus
Hoofdstuk 1 : Krachten, spanningen en rekken
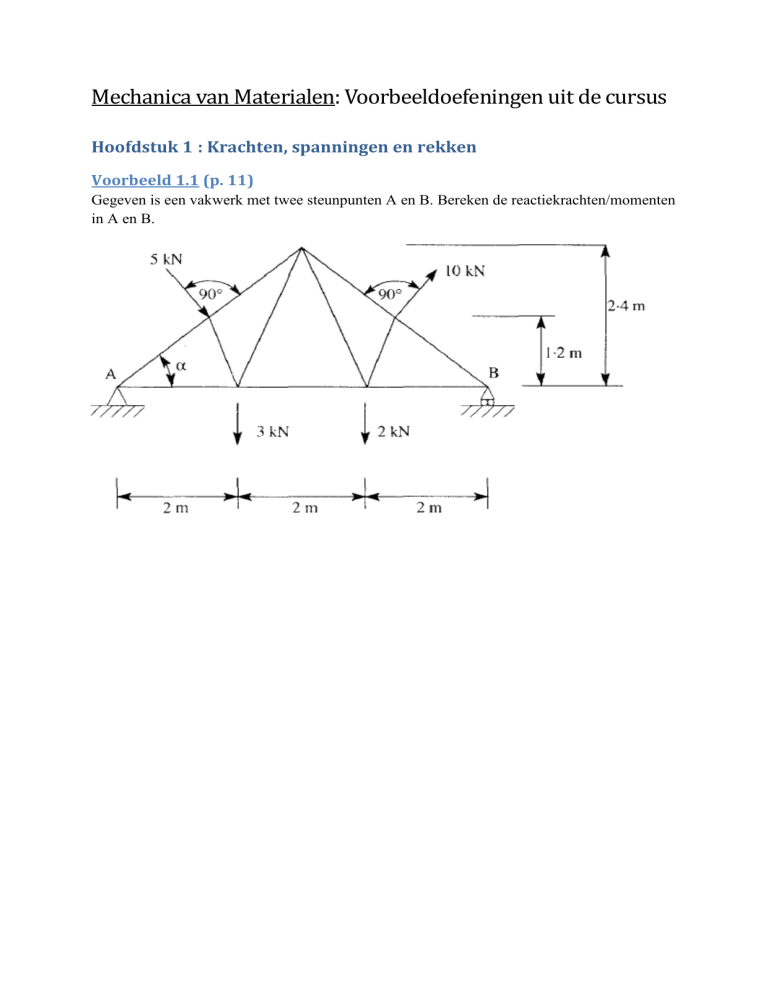
Voorbeeld 1.1 (p. 11)
Gegeven is een vakwerk met twee steunpunten A en B. Bereken de reactiekrachten/momenten
in A en B.
Voorbeeld 1.2 (p. 16)
Bepaal de resulterende inwendige belastingen die in het punt B op de dwarsdoorsnede van de
pijp werken. De pijp heeft een massa van 2 kg/m en wordt aan het uiteinde A belast door een
verticale kracht van 50 N en een koppel van 70 Nm. De pijp is bij C vast aan de muur
bevestigd.
Voorbeeld 1.3 (p. 17) Examen 1ste zittijd AJ 2002-2003. 35 minuten
Alle staven in onderstaand vakwerk zijn scharnierend met elkaar verbonden. In twee knopen
grijpt een neerwaarts gerichte puntlast aan van respectievelijk 0,75 P en P. Bepaal de positie
van de staaf die de grootste kracht moet dragen.
Voorbeeld 1.4 (p. 30)
De houten steun in onderstaande figuur hangt aan een stalen staaf van 10 mm diameter, die
aan de muur is bevestigd. De steun draagt een verticale belasting van 5 kN. Bereken de
gemiddelde schuifspanning in de staaf bij de muur en langs de twee gearceerde vlakken van
de steun, waarvan er één met abcd is gemarkeerd.
Voorbeeld1.5 (p. 54)
Een koperen staaf ondervindt een constante druk langs de randen, zoals aangegeven in
onderstaande figuur. Als de staaf een lengte a = 300 mm, breedte b = 50 mm en dikte t = 20
mm heeft vóórdat de belasting wordt aangebracht, bepaal dan de nieuwe lengte, breedte en
dikte bij belasting. Neem Ecu = 120 GPa en υcu = 0,34.
Voorbeeld 1.6 (p. 68)
Een betonnen kolom met een vierkante dwarsdoorsnede van 50 cm bij 50 cm, is gewapend
met vier stalen staven, elk met een diameter van 2,5 cm. De staven zijn ingebetonneerd bij de
vier hoeken van de kolom. Als de E-modulus van staal 200 GPa bedraagt en deze van beton
14 GPa, bereken dan de drukspanningen in het staal en het beton als de totale drukkracht op
de kolom 1 MN (106 N) bedraagt.
Voorbeeld 1.7 (p. 72)
Een starre, onvervormbare balk is bevestigd op de bovenzijde van drie kolommen. De
middelste kolom bestaat uit aluminium (Ealu = 70 GPa, αalu = 23*10-6 m/m*°C), de twee
buitenste kolommen uit staal (Est = 200 GPa, αst = 12*10-6 m/m*°C). De kolommen hebben
elk een onbelaste lengte van 250 mm en de temperatuur is T1 = 20 °C. bepaal de kracht in elke
kolom als de balk wordt onderworpen aan een constant verdeelde belasting van 150 kN/m en
de temperatuur tot T2 = 80 °C wordt verhoogd.
Hoofdstuk 2 : Structureel gedrag
Voorbeeld 2.1 (p. 94)
Bepaal de hoofdtraagheidsassen voor het volgend profiel
Bereken de traagheidsmomenten opnieuw m.b.v. het draadmodel
Voorbeeld 2.2 (p. 108) Examen 1e zittijd 2002-2003, 35 minuten
Gegeven is de volgende balk
Op x = 2 m bevindt zich een neerwaartse puntlast van 10 kN, en tussen x = 4 m en x = 5 m
bevindt zich een gelijkmatig verdeelde belasting van 15 kN/meter. Teken de dwarskracht- en
momentenlijn.
Voorbeeld 2.3 (p. 114)
Een balk heeft het volgende trapeziumvormig profiel in het y-z vlak:
Als deze doorsnede belast wordt met een moment M = 22,5 kNm, bereken dan de plaats en de
waarde van de maximale normaalspanning.
Voorbeeld 2.4 (p. 118)
Bepaal de verdeling van de schuifspanningen
in het rekhoekig profiel:
Voorbeeld 2.5 (p. 124)
Een balk is onderaan ingeklemd en op de twee dwarsbalken grijpt links een kracht 2F aan, en
rechts een kracht F. de richting en zin van de krachten is zoals getekend op de figuur. De
dwarsdoorsnede van de balk is een regelmatige zeshoek en is in elke sectie van de verticale en
horizontale balken constant:
Als volgende waarden gegeven zijn:
F = 1 kN
L=1m
a = 30 cm
E = 200 GPa
bereken dan de totale verticale en horizontale verplaatsing van het punt C.
Voorbeeld 2.6 (p.129)
Bepaal de helling en de doorbuiging van de as bij elk van de poelies C, D en E. De as is
gemaakt van staal en heeft een diameter van 30 mm. De lagers bij A en B oefenen slechts
verticale reacties op de as uit. Est = 200 GPa.
Hoofdstuk 3 Oplossingsmethodes
Hoofdstuk 4 Tweedimensionale elastische problemen
Voorbeeld 4.1 (p.166)
In het punt P bestaat de volgende spanningstoestand in het assenstelsel (x,y,z):
Op welk vlakje van P zal met de grootste schuifspanning vinden?
Voorbeeld 4.2 (p.171)
Gegeven is de volgende vervormingstoestand:
De overige rekcomponenten zijn nul.
a) Welke bijzondere toestand is dit?
b) Bepaal de hoofdrekken m.b.v. de cirkel van Mohr. De berekende waarden moeten
exact zijn.
c) Als E = 200 GPa en = 0,3 bepaal dan de hoofdspanningen. Teken twee vierkantjes
waarop u de oriëntatie aanduidt van het oude x-y assenstelsel en van het nieuwe
assenstelsel van de hoofdspanningen. Teken ook de richting en zin van de
hoofdspanningen. De spanningen van het x-y assenstelsel hoeft u niet te berekenen.
Voorbeeld 4.3 (p. 184) Examen 1e zittijd 200-2003, voorziene tijd: 50 min.
Gegeven zijn twee dunne schijven met volgende afmetingen:
De materiaalparameters zijn:
Aluminium:
E1 = 72 GPa
= 0,3
= 23,0 ∙ 10 /°C
Staal:
E2 = 200 GPa
= 0,3
= 11,0 ∙ 10 /°C
Gevraagd:
a) Als de temperatuur verhoogt van 20°C naar 80°C, wat is dan de contactspanning
tussen de aluminium schijf en de stalen schijf?
b) Als de temperatuur gehandhaafd blijft op 80°C, welke bijkomende radiale
drukspanning moet men opleggen aan de buitenrand van de stalen schijf opdat de
contactdruk tussen de aluminium schijf en de stalen schijf precies -100 MPa zou
bedragen
Voorbeeld 4.4 (p.193) Examen 1e zit 2002-2003, voorziene tijd: 35 min.
Gegeven is een dunne stalen schijf, langs zijn buitenrand ingeklemd in een starre wand:
De binnenstraal van de schijf is 100 mm, de buitenstraal 200 mm. De eigenschappen van het
staal zijn:
E = 200 GPa
= 0,3
= 11,0 ∙ 10 /°C
Bij een omgevingstemperatuur van 20°C is de stalen schijf spanningsloos. Als men aan de
binnenrand van de schijf een temperatuur oplegt van 50°C en aan de buitenrand een
temperatuur van 100°C, wat is dan de contactspanning tussen de stalen schijf en de starre
wand (die niet vervormt bij de verhoogde temperatuur)?
Hoofdstuk 5 Mechanische eigenschappen en materiaalmodellen
Voorbeeld 5.1 (p.240)
In het punt A op het vrij oppervlak van een machineonderdeel wordt een rekstrookrozet
gekleefd. Voor de drie rekstroken R1, R2 en R3 geldt de volgende tabel:
a) Zoek de componenten ( ,
,
) van de rektensor in het punt A. aanwijzing: zoek
eerst deze rekcomponenten in een gunstig te kiezen assenstelsel (x’,y’)
b) Bepaal de rekcomponenten ( , , ) uit het vlak als de materiaalconstanten E
=210 GPa en = 0,3 zijn.