10 Afstanden - de Wageningse Methode

28
1
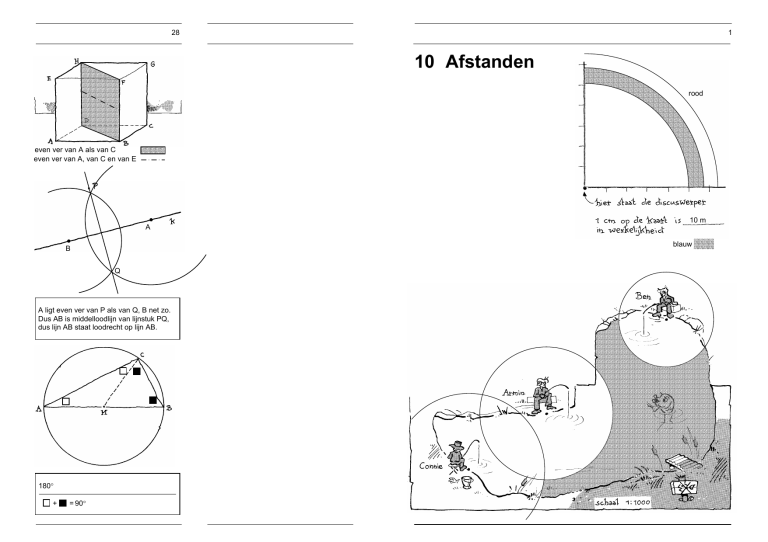
10 Afstanden
rood
even ver van A als van C
even ver van A, van C en van E
A
blauw
B
Q
A ligt even ver van P als van Q, B net zo.
Dus AB is middelloodlijn van lijnstuk PQ,
dus lijn AB staat loodrecht op lijn AB.
180°
+ = 90°
10 m
2
26
27
A
groen
blauw
groen
blauw
schaal
1000
1: ________
de punten A en B rood
Bijvoorbeeld de stippellijn
M
Bijvoorbeeld de stippellijn
Bijvoorbeeld de stippellijn
schaal 1 :
500
B
rood
24
25
3
4
rood
B
11 cm
rood
11 cm
A
S
groen
Die liggen even ver van beide benen.
Het middelpunt ligt op het midden van de
schuine zijde (ABC is halve rechthoek).
C
De straal is de helft van de lengte van de
schuine zijde, hier dus 21 cm.
∠ABS = 1 ⋅ 37° = 181°, ∠BAS = 1 ⋅ 90° = 45°,
dus ∠ASB = 180° – (181° + 45°) = 1161°.
∠SCB = 1 ⋅ (180° – 37° – 90°) = 261°, dus
∠CSB = 180° – (261° + 181°) = 135° en
∠CSA = 360° – 135° – 1161° = 1081°.
50°
35°
D
Een vlieger
AC = BC, want C ligt op de middelloodlijn.
Driehoek ABC is dus gelijkbenig, dus
∠ABC = 50°; ∠ACB = 180° – 2 ⋅ 50° = 80°.
∠ADB = 360° – (2 ⋅ 85° + 80°) = 110°.
een zijde van een driehoek is een
lijnstuk
bisssectrice
van p en q
een ribbe van een piramide is een
lijnstuk
middelloodlijn
van K en L
M
een been van een hoek is
halve lijn
bisssectrice
van p en q
Dat is het snijpunt van de diagonalen.
Nee, de cirkel door A, B en C gaat niet
door D.
potlood
blauw
rood
Langs een van de getekende stippellijnen
kun je meten: 2,4 cm, dat is 288 km
lijnstuk CD
5
6
22
23
MIDDELLOODLIJN
Op de middelloodlijn van lijnstuk AB liggen
de punten die even ver van A als van B liggen.
oneindig dun
S
oneindig veel
Je
kunt
een
middelloodlijn
met
je
geodriehoek tekenen of met passer en liniaal.
De drie middelloodlijnen van een driehoek
gaan door één punt. Dit punt ligt even ver
van de hoekpunten van de driehoek.
∠SAD = 1 ⋅ 51° = 251°
∠ADC = 180° – 51° = 129°
∠ADS = 1 ⋅ 129° = 641°
INGESCHREVEN CIRKEL
blauw
rood
∠ASD = 180° – 251° – 641° = 90°
Zie plaatje:
oneindig veel
= 90° (overstaande hoeken), de andere hoeken
van de vierhoek zijn ook recht, dus rechthoek.
nee
De ingeschreven cirkel van een driehoek is de
cirkel die de zijden van die driehoek raakt.
Het is dus de grootste cirkel die je binnen de
driehoek kunt tekenen
Teken een (niet al te kleine) driehoek. Teken
de ingeschreven cirkel van die driehoek, zoek
eerst het middelpunt van die cirkel.
MET PASSER EN LINIAAL
Teken met vier boogjes (op een kladblaadje) :
ja
ja
M
blauw
rood
- de loodlijn vanuit een punt P op een lijn k,
- de middelloodlijn van een lijnstuk AB,
- de bissectrice van een hoek A .
20
21
8
middelloodlijn van BC
A
M
7
middelloodlijn van AC
straal
M
B
C
Op de kaart is de weg 2,8 cm lang, dus in
werkelijkheid 4,2 km.
middelloodlijn RQ
middelloodlijn PR
22 a 23 mm
18 mm
V1
V2
M
S
∠ABC = 50°, want driehoek ABC is gelijkbenig,
∠ACB = 180° – 2 ⋅ 50° = 80°
∠SAB = 1 ⋅ 50° = 25°, want lijn AS is de bissectrice
van hoek CAB. Net zo is ∠SBA = 25°.
∠ASB = 180° – 2 ⋅ 25° = 130°
schaal 1 :
1 cm van
P en 3 cm
van Q
CS bissectrice van hoek C, dus ∠ACS = 1 ⋅ 80°= 40°.
∠ASC = 180° – 25° – 40° = 115°
400000
3 cm
6 cm van
P en 2 cm
van Q
2 cm
Omdat de drie bissectrices door één punt gaan.
straal
AC = BC, verder AS = BS, want driehoek ASB is gelijkbenig, dus C en S liggen even ver van A als van B.
Q
27 mm
één
één
Q
9
10
18
put
19
bissectrice
bissectrice
m staat loodrecht op lijnstuk AB;
m gaat door het midden van lijnstuk AB.
middelloodlijn van AC
middelloodlijn van AB
Z
groen
rood
vijf nieuwe punten
3 cm op het kaartje, dat is 6 km in
werkelijkheid.
middelloodlijn van AB
A
B
middellloodlijn van BC
C
16
17
11
12
D
Station
S
B
C
De hoeken a en b zijn even groot, want
m is de bissectrice van de hoek
De hoeken c en d zijn even groot, want n
is de bissectrice van de hoek
S is rood gekleurd, dus S ligt even ver
AB als van lijn AC
van lijn ____
___.
R
rood
blauw
S is blauw gekleurd, dus S ligt even ver
180°
gestrekte hoek
BC
AB als van lijn ___.
van lijn ___
40°
50°
Dus ligt S ook even ver van lijn AC als
de bissectrice
van lijn BC, dus ligt S op _________________
180 : 2 = 90°
van
hoek C
___________________.
rood
blauw
potlood
X
De rode punten liggen even ver ____
van A als van B
_________________________________________
blauw
liggen even ver
De blauwe punten _____________________
van
B als van C
________________________________________
rood
S is rood gekleurd, dus S ligt even ver
S
M
A als van ___.
B
van ___
S is blauw gekleurd, dus S ligt even ver
C
B als van ___.
van ___
∆PQS is zowel rood als
blauw gekleurd
Dus ligt S ook even ver van A als van C,
middelloodlijn van AC
dus ligt S op de _________________________
Y
13
14
15
rood
blauw
achtste
A
B
k ligt even ver van A als van B.
rood
44°
blauw
schaal 1 : 200
Die twee afstanden zijn gelijk
rood
blauw
19 mm
22°
Dat ligt 2 cm van k; bovendien ligt het
even ver van k als van m, dus ligt het ook
2 cm van m.
124°
62°
S
lijkt 90°