Wiskunde SO b

Wiskunde SO b
Klas 3 Hoofdstuk 11 TL
Uitwerking
1
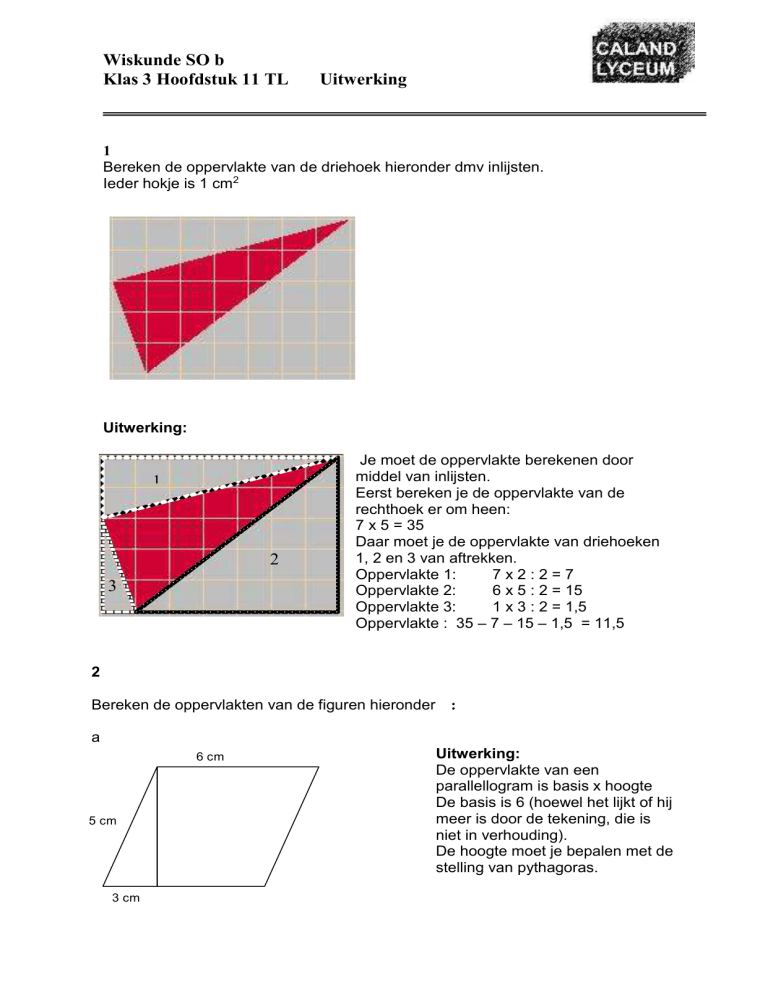
Bereken de oppervlakte van de driehoek hieronder dmv inlijsten.
Ieder hokje is 1 cm2
Uitwerking:
1
2
3
Je moet de oppervlakte berekenen door
middel van inlijsten.
Eerst bereken je de oppervlakte van de
rechthoek er om heen:
7 x 5 = 35
Daar moet je de oppervlakte van driehoeken
1, 2 en 3 van aftrekken.
Oppervlakte 1:
7x2:2=7
Oppervlakte 2:
6 x 5 : 2 = 15
Oppervlakte 3:
1 x 3 : 2 = 1,5
Oppervlakte : 35 – 7 – 15 – 1,5 = 11,5
2
Bereken de oppervlakten van de figuren hieronder
:
a
6 cm
5 cm
3 cm
Uitwerking:
De oppervlakte van een
parallellogram is basis x hoogte
De basis is 6 (hoewel het lijkt of hij
meer is door de tekening, die is
niet in verhouding).
De hoogte moet je bepalen met de
stelling van pythagoras.
rechthoekzijde kwadraat
3 9
4 16
5 25
De hoogte is dus 4
De Oppervlakte is basis x hoogte = 6 x 4 = 24 cm2
b
5 cm
15 cm
Uitwerking:
Oppervlakte driehoek is basis x hoogte : 2.
Neem 5 als basis en bereken eerst hoogte met behulp van de stelling van
pythagoras
rechthoekzijde kwadraat
5 25
14,14 200
15 225
De oppervlakte van de driehoek is dus : 5 x 14,14 : 2 = 35,35 cm2
3
2m
3m
9m
5,5 m
Het huis hierboven heeft de vorm van een prisma
a) welk grensvlak kun je dan als “bodem” nemen?
b) Bereken de inhoud van dit prisma
Uitwerking:
a) De voorgevel van het huis.
(het gekleurde deel)
2m
b)
Eerst moet je de oppervlakte van
3m
de bodem berekenen. Die is
samengesteld uit een rechthoek
5,5 m
en een driehoek.
2
Oppervlakte rechthoek:
3 x 5,5 = 16,5 m
Oppervlakte driehoek:
basis x hoogte : 2
2
Dus: 5,5 x 2 : 2 = 5,5 m
Samen vormen ze de oppervlakte van de bodem: 16,5 + 5,5 = 22 m2
De inhoud van een prisma is oppervlakte bodem x hoogte.
De hoogte is 9 m
Inhoud huis:
22 x 9 = 198 m3
4 Bereken de inhoud van deze piramide:
6 dm
5 dm
4 dm
Uitwerking:
De inhoud van een piramide is oppervlakte grondvlak x hoogte : 3
Het grondvlak is een rechthoek met oppervlakte: 4 x 5 = 20 dm2
De inhoud van de piramide is:
20 x 6 : 3 = 40 dm3
9m