Interimtoets TBS 1 2009 Versie A Antwoorden

Interim Toegepaste Biostatistiek deel 1
14 december 2009
Versie A
ANTWOORDEN
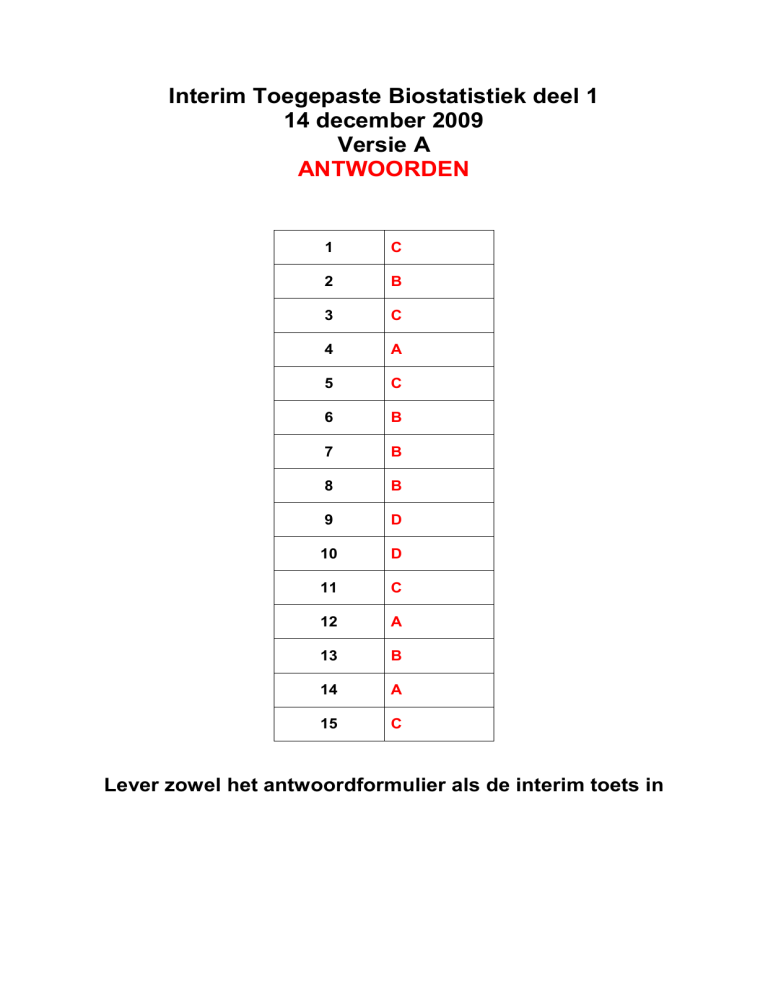
1
C
2
B
3
C
4
A
5
C
6
B
7
B
8
B
9
D
10
D
11
C
12
A
13
B
14
A
15
C
Lever zowel het antwoordformulier als de interim toets in
Versie A
1.
2.
3.
4.
5.
6.
7.
2
Dit tentamen bestaat uit 15 meerkeuzevragen, waarvan steeds 1
antwoord goed is.
Tenzij anders is vermeld gebruik je bij het toetsen een significantie
niveau van 5%
Vul op het antwoordformulier je naam en studentnummer in.
Controleer het versie nummer op het antwoordvel en de interimtoets.
Kruis eerst de juiste antwoorden in de interim toets aan en pas op het
einde de juiste antwoorden op het antwoordformulier.
Fraude wordt bestraft.
Succes!
1.
Welke bewering over het vergelijken van twee onafhankelijke steekproeven is NIET JUIST.
A.
B.
C.
D.
De Levene’s test wordt gebruikt om twee varianties te testen.
De onderliggende voorwaarde van de Mann-Whitney toets is dat de verdelingen van
de data in beide groepen gelijk moeten zijn.
Het aantal waarnemingen in beide groepen moet gelijk zijn.
De Mann-Whitney toets wordt gebruikt om de mediane waarden van twee groepen
met elkaar te vergelijken.
De enige voorwaarden die gelden bij de ongepaarde t-toets is de normaliteit van de
residuen, de gelijkheid van de varianties, additief model en onafhankelijkheid. Bij de MannWhitney is de enige voorwaarde dat de verdelingen gelijk moeten zijn. Dus in beide gevallen
worden er geen voorwaarden gesteld voor het aantal waarnemingen in een groep.
2.
Welk van de onderstaande beweringen is JUIST:
A.
B.
C.
D.
Een nominale variabele heeft categorieën die geordend zijn.
Een ratio/interval variabele heeft numerieke waarden.
Bij een ordinale variabele zijn de afstanden tussen de categorieën gelijk.
Een ratio variabele is altijd continu.
Alternatief A is fout want de nominale variabele is de enige type variabele die geen
ordening heeft. Alternatief C is ook fout want een ordinale variabele kan ook niet
numeriek zijn of geen numerieke betekenis hebben. Tenslotte is alternatief D ook fout
want een ratio variabele kan ook discreet zijn (denk aan tellingen: aantal bladeren
aan een zaailing bijvoorbeeld).
3.
Lepomis macrochirus is een straalvinnige vis uit de familie van zonnebaarzen
(Centrarchidae). We veronderstellen dat de lengte van een populatie L. macrochirus normaal
verdeeld is met gemiddelde 152.1 mm en standaardafwijking 19.6 mm. Welke bewering is
JUIST?
A
B.
C.
In een steekproef van 40 vissen uit deze populatie zal de schatting van de
standaardafwijking altijd kleiner zijn dan in een steekproef van 10 vissen.
Ongeveer 95% van de buisjes heeft een lengte tussen 132.5 mm en 171.7 mm.
Prob(X > 214.8) is gelijk aan Prob(Z > 3.2) waarbij Z standaard normaal verdeeld is.
Versie A
D.
3
Bij 13.4% van aselect gekozen vissen zal de lengte kleiner zijn dan 122.7 mm.
A is fout want de SEM wordt kleiner maar niet per se de SD.
B is fout want gegeven is het interval gemiddelde ± SD en daartussen valt ca 68% van de
data en geen 95%
D is fout want de gegeven kans is de tweezijdige kans en gevraagd werd de eenzijdige kans
De vragen 4 en 5 hebben betrekking op het volgende onderzoek met bijbehorende
SPSS uitvoer.
Een onderzoeker gaat de werkzaamheid van een groeihormoon preparaat onderzoeken. Een
groep van genetisch gelijke ratten wordt aselect in twee groepen verdeeld. De eerste groep
ratten krijgt 3 maanden lang een placebo, de tweede groep krijgt 3 maanden lang het
groeipreparaat. Na 3 maanden worden de ratten gewogen om te kijken of de ratten in de
tweede groep inderdaad meer gegroeid zijn dan de ratten in de eerste groep.
Group Statistics
toename gewicht
groep
placebo
groeipreparaat
N
Mean
257.6609
266.4152
10
10
Std. Deviation
11.91587
9.52502
Std. Error
Mean
3.76813
3.01208
Independent Samples Test
Levene's Test for
Equality of Variances
F
toename gewichtEqual variances
assumed
Equal variances
not assumed
.678
Sig.
.421
t-test for Equality of Means
t
Mean
Std. Error
Sig. (2-tailed) Difference Difference
df
-1.815
18
.086
-8.75430
4.82404 -18.88924
1.38064
-1.815
17.167
.087
-8.75430
4.82404 -18.92460
1.41601
4.
Bereken voor de groeipreparaat groep een 99% betrouwbaarheidsinterval voor het
gemiddelde gewichtstoename.
A.
B.
C.
D.
[256.63; 276.20]
[256.87; 275.96]
[258.66; 274.17]
[259.61; 273.23]
t verdeling met df = 9 en α= 1%
t verdeling met df = 10 en α= 1%
z verdeling met α= 1%
t verdeling met df = 9 en α= 5%
5.
Wat zijn de getoetste hypotheses?
A.
B.
C.
D.
H0: µ1 = µ2, H1: µ1 ≠ µ2
H0: µ1 ≠ µ2, H1: µ1 = µ2
H0: µ1 ≥ µ2, H1: µ1 < µ2
H0: µ1 ≤ µ2, H1: µ1 > µ2
95% Confidence
Interval of the
Difference
Lower
Upper
Versie A
4
De toets is eenzijdig en je verwacht gemiddelde toename gewicht is in groep 2 groter
6.
In een bepaald soort kunstmest zou volgens de fabrikant 0,1 mg werkzame stof moeten
zitten. Met behulp van een aselecte steekproef wordt nagegaan of dit gemiddeld genomen
wel correct is (α =0,05). Het gevonden gemiddelde blijkt gelijk te zijn aan 0,087 mg. Verder
wordt de volgende SPSS-output gemaakt. Kan met deze output een conclusie worden
getrokken over het accepteren of verwerpen van de nulhypothese (µ=0,1 mg)?
One-Sample Test
Test Value = 0
Werkzame stof
A.
B.
C.
D.
t
5.553
df
6
Sig.
(2-tailed)
,001
Mean
Difference
,087
95% Confidence Interval
of the Difference
Lower
Upper
0.0487
0.1255
ja, een conclusie kan door de foutief opgegeven referentiewaarde van 0 wel uit de
gegeven p-waarde, maar niet uit het 95%-betrouwbaarheidsinterval worden
getrokken
ja, een conclusie kan door de foutief opgegeven referentiewaarde van 0 wel uit het
95%-betrouwbaarheidsinterval, maar niet uit de gegeven p-waarde worden getrokken
ja, een conclusie kan zowel uit de gegeven p-waarde als uit het 95%betrouwbaarheidsinterval worden getrokken
nee, een conclusie kan door de foutief opgegeven referentiewaarde van 0 in zijn
geheel niet worden getrokken
De gegeven p-waarde is de p-waarde die hoort bij de nulhypothese µ=0 en niet bij µ=0.1.
Wat je wel zou kunnen zeggen is dat de juiste p-waarde groter zal zijn dan 0.001 maar
hoeveel groter weet je niet.
Het betrouwbaarheidsinterval geeft aan wat het mogelijke populatie gemiddelde met een
zekere betrouwbaarheid zou kunnen zijn. Omdat de Test Value gelijk is aan 0 is het gegeven
interval gelijk aan het 95% betrouwbaarheidsinterval voor het verschil. De waarde µ=0.1 ligt
in dit interval dus het populatie gemiddelde zou 0.1 kunnen zijn. Dus die nulhypothese zou je
dan niet mogen verwerpen.
Een andere benadering is: het gegeven betrouwbaarheidsinterval geeft alle waarden voor µ0
aan waarvoor je de nulhypothese H0: µ - “test value” = µ0 niet zou gaan verwerpen (zie ook
opgave 4 uit werkcollege 5). In dit geval is test value gelijk aan 0 dus geldt het gegeven
betrouwbaarheidsinterval voor het toetsen van de nulhypothese H0: µ = µ0. De waarde µ=0.1
ligt in dit interval, dus de nulhypothese mag je dus verwerpen.
7.
Veronderstel dat een bioloog de uitspraak doet dat het verschil tussen twee
steekproefgemiddelden “statistisch significant is op het 5% niveau”. Wat bedoelt hij dan
precies?
A.
B.
C.
D.
Er is tenminste 95% kans dat er een reёel verschil is tussen de gemiddelden in de
beide populaties
De p-waarde voor de nulhypothese H0: µ1 = µ2 is 5% of minder
Het waargenomen verschil wijkt minder dan 5% af van het biologisch relevante
verschil.
Er is een verschil van minder dan 5% tussen de steekproefgemiddelden.
Versie A
5
Alternatief A is fout want je gaat uit van de nulhypothese en niet van de alternatieve
hypothese. Ook ga je bij het toetsen geen uitspraken doen over de grootte van het verschil
maar alleen of het afwijkt van nul of niet. Of een verschil reëel is hangt ook heel sterk af van
wat biologisch relevant is. De uitspraak van de onderzoeker heeft te maken met het toetsen,
en zegt dus niets over het verschil tussen waargenomen verschil en het biologisch relevante
verschil (alternatief C) of de grootte van het waargenomen verschil (alternatief D).
8.
Bewering 1: de standaardfout van het gemiddelde (SEM) is een maat voor de precisie
waarmee het populatiegemiddelde geschat wordt.
Bewering 2: de standaardfout van het gemiddelde (SEM) kan alleen worden geschat als we
herhaalde steekproeven uit de populatie nemen.
A.
B.
C.
D.
beide beweringen zijn juist
bewering 1 is juist en bewering 2 is onjuist
bewering 1 is onjuist en bewering 2 is juist
beide beweringen zijn onjuist
We schatten juist altijd een standaardfout op basis van één steekproef! Alleen de theorie
over de SEM zich gedraagt is gebaseerd op oneindig vele steekproeven.
9.
Twee onderzoekers verrichten allebei bloeddrukmetingen met een kwikmanometer.
Onderzoeker A leest de bloeddruk nauwkeurig af (dus precisie is goed), echter van zijn
bloeddrukmeter geeft de schaal de bloeddruk gemiddeld 10 mm Hg te hoog aan (dus bias).
Onderzoeker B gaat minder nauwkeurig te werk (geen precisie) en gebruikt een
bloeddrukmeter die de bloeddrukhoogte goed weergeeft (geen bias).
De resultaten van onderzoeker A hebben naar verwachting, ten opzichte van B:
A.
Een kleinere bias en een slechtere precisie
B.
Een kleinere bias, maar een betere precisie
C.
Een grotere bias en een slechtere precisie
D.
Een grotere bias, maar een betere precisie
10.
Het effect van drie verschillende antibiotica op de groei van een bacteriekolonie wordt
onderzocht. De antibiotica worden toegevoegd aan petrischalen en vervolgens worden de
schalen geïnfecteerd met de bacteriekolonie. Ook is een controlegroep gebruikt, waarbij
geen antibioticum is toegevoegd. Na drie dagen is de diameter van de bacteriekolonies (in
mm) gemeten. Op basis van de getoonde boxplot, welke van onderstaande beweringen is
NIET JUIST?
Versie A
A.
B.
C.
D.
6
De waarnemingen in de controlegroep en de groepen met antibioticum A of C zijn
nagenoeg symmetrisch verdeeld
De groep met antibioticum A heeft de laagste mediaan
De groep met antibioticum C heeft de kleinste interkwartielafstand
De waarnemingen in de groep met antibioticum B zijn links scheef verdeeld
De waarnemingen zijn juist rechts scheef verdeeld.
De vragen 11, 12 en 13 hebben betrekking op het volgende onderzoek met
bijbehorende SPSS uitvoer.
Wat is de invloed van rondwormen op de groei van planten? Een bioloog bereid 16 identieke
potten voor en voegt verschillende aantallen rondwormen toe aan de potten. Dan verdeelt hij
16 identieke tomatenzaailingen over de potten. Na 16 dagen meet hij de toename in lengte
van de planten. De onderzoekers hebben de data in SPSS geanalyseerd. De analyse staat
hieronder weergegeven.
Descriptives
groei zaalingen (cm)
N
0
1000
5000
10000
Total
4
4
4
4
16
Mean Std. Deviation Std. Error
10.650
2.0535
1.0267
10.425
1.4863
.7432
5.600
1.2437
.6218
5.450
1.7711
.8855
8.031
2.9886
.7471
95% Confidence Interval for
Mean
Lower Bound Upper Bound Minimum Maximum
7.382
13.918
9.1
13.5
8.060
12.790
8.2
11.3
3.621
7.579
4.6
7.4
2.632
8.268
3.2
7.5
6.439
9.624
3.2
13.5
Versie A
7
Levene's Test of Equality of Error Variances a
Dependent Variable: groei zaalingen (cm)
F
df1
.286
df2
3
Sig.
.834
12
Tests the null hypothesis that the error variance of
the dependent variable is equal across groups.
a. Design: Intercept+nematoden
Tests of Between-Subjects Effects
Dependent Variable: groei zaalingen (cm)
Source
Corrected Model
Intercept
nematoden
Error
Total
Corrected Total
Type III Sum
of Squares
100.647a
1032.016
100.647
33.328
1165.990
133.974
df
3
1
3
12
16
15
Mean Square
33.549
1032.016
33.549
2.777
F
12.080
371.591
12.080
Sig.
.001
.000
.001
a. R Squared = .751 (Adjusted R Squared = .689)
Tests of Normality
a
Residual for groei
Kolmogorov-Smirnov
Statistic
df
Sig.
.091
16
.200*
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
Shapiro-Wilk
Statistic
df
.971
16
Sig.
.859
Versie A
8
11.
Welke van de onderstaande beweringen is JUIST?
A.
De range in de groep zaailingen zonder nematoden is 6.536.
B.
De gepoolde standaardafwijking van de vier groepen is 2.9886.
C.
De variantie in de groep zaailingen met 5000 nematoden is 1.547.
D.
Er is geen verschil tussen de vier groepen want het gemiddelde 8.031 ligt in het 95%
betrouwbaarheidsinterval [6.439; 9.624]
De juiste range is 4.4 (alternatief A).
In alternatief B is de standaardafwijking gegeven als je alle waarnemingen als 1 groep
beschouwd. De echte gepoolde standaardafwijking is 1.6665 (de wortel van de MSerr).
Alternatief D is pure onzin: een steekproef gemiddelde ligt altijd precies in het midden van
het betrouwbaarheidsinterval voor het populatie gemiddelde.
12.
Welke van de onderstaande beweringen is JUIST?
A.
De overschrijdingskans van de ANOVA is 0.001.
B.
Je mag geen ANOVA uitvoeren op deze data omdat de varianties significant
verschillen.
C.
Op basis van de Q-Q plot kun je concluderen dat de variabele ‘groei’ nagenoeg
normaal verdeeld is.
D.
De toetsingsgrootheid van de ANOVA is 371.591.
Alternatief B is fout want de Levene toets geeft juist aan dat de variantie wel homogeen zijn,
de p-waarde is immers groter dan 0.05.
Alternatief C is ook fout want de Q-Q plot zegt alleen maar dat de residuen van het ANOVA
model normaal verdeeld zijn en zegt dus niets over de verdeling van de groei zelf. (Zie
werkcollege 7, vraag 4b en antwoord daarop.)
Versie A
9
Alternatief D is ook fout want de toetsgrootheid om te toetsen of er verschillen zijn tussen de
viertal aantallen rondwormen is gelijk aan 12.080.
13.
De onderzoekers willen post-hoc toetsen (met Bonferroni correctie) uitvoeren om de
verschillen tussen alle groepen te bekijken. Geef de toetsingsgrootheid en de (geschatte)
kritieke waarde voor de vergelijking van het gemiddeld verschil in groei tussen de groep
zaailingen met 5.000 en de groep zaailingen met 10.000 nematoden.
A.
B.
C.
D.
t = 0.127, kritieke waarde is ongeveer 2.179
t = 0.127, kritieke waarde is ongeveer 3.055
t = 0.139, kritieke waarde is ongeveer 2.179
t = 0.139, kritieke waarde is ongeveer 3.055
LSD toets zonder Bonferroni
LSD toets met Bonferroni
t toets zonder Bonferroni
t toets met Bonferroni
Gevraagd worden post hoc toetsen, dus de LSD toets gebruiken en niet de t-toets voor 2
onafhankelijke groepen (zie onder andere opgave 5 uit werkcollege 7). Verder zijn er totaal
6 paarsgewijze vergelijkingen die worden uitgevoerd. Dus bij het toetsen met Bonferroni
correctie ga je niet werken met een tweezijdige α van 5% maar met een α van 5%/6 = 0.83%
14.
Blootstelling aan lood heeft een effect op neuromusculaire verbindingen en veroorzaakt
myopathie (ziekte van het spierweefsel). Antioxidanten zoals ascorbinezuur beschermen
mogelijk tegen myopathie. Om het effect van ascorbinezuur op door lood veroorzaakte
myopathie te onderzoeken voert een onderzoeker het volgende experiment uit. Bij 12 aan
lood blootgestelde ratten wordt de isometrische spierspanning in de tibialis anterior gemeten.
Na toediening van ascorbinezuur wordt de spierspanning opnieuw gemeten. De onderzoeker
verwacht dat de spierspanning als gevolg van het geven van ascorbinezuur afneemt.
Hieronder staan de door de onderzoeker verzamelde gegevens. Voer de juiste t-toets uit en
beslis of er sprake is van een significante afname van de spierspanning.
Rat nr.
Spierspanning
vooraf (g)
Spierspanning
na toediening van
ascorbinezuur (g)
verschil
1
3
3
0
2
2
3
1
3
4
3
-1
4
3
2
-1
5
3
3
0
6
4
3
-1
7
2
1
-1
8
4
4
0
9
4
5
1
10
3
0
-3
11
3
1
-2
12
3
1
-2
Versie A
10
Opzet is gepaard dus de gepaarde t-toets moet worden gebruikt. Er zijn geen aanwijzingen
dat de verschillen niet normaal verdeeld zouden zijn. Gemiddeld verschil is -0.75 met een SD
van 1.215. Dit geeft een toetsingsgrootheid van T=-2.138. De toets was eenzijdig dus de pwaarde is 0.025<p<0.05.
Welke bewering is JUIST
A.
B.
C.
D.
0.025 < p < 0.05, er is dus wel sprake van een significante afname.
0.025 < p < 0.05, er is dus geen significante afname gevonden op basis van deze
gegevens.
0.05 < p < 0.10, er is dus wel sprake van een significante afname.
0.05 < p < 0.10, er is dus geen significante afname gevonden op basis van deze
gegevens.
Alternatief B en C zijn fout vanwege de verkeerde link tussen de grootte van de p-waarde en
het al dan niet verwerpen van je nulhypothese. In het algemeen geldt als de p-waarde lager
is dan je gestelde significantie nivo (meestal 5%) dan verwerp je je nulhypothese. Dan is er
sprake van ‘significant’ verschil. Het foute alternatief D krijg je als je of 1) tweezijdig gaat
toetsen of 2) de ongepaarde t-toets hebt gebruikt maar wel eenzijdig.
15.
Een arts meet kwaliteit van leven op een schaal van 0 tot 100 bij 3 groepen patiënten. Hij wil
onderzoeken of de kwaliteit van leven van deze groepen patiënten verschilt. Hieronder is een
deel van de analyse welke in SPSS is uitgevoerd weergegeven.
Versie A
11
Levene's Test of Equality of Error Variances a
Dependent Variable: kwaliteit
F
df1
.000
df2
2
297
Sig.
1.000
Tests the null hypothesis that the error variance of
the dependent variable is equal across groups.
a. Design: Intercept+group
Welke toets moet de arts toepassen?
A.
B.
C.
D.
variantie-analyse (ANOVA)
variantie-analyse (ANOVA) op de logaritmisch-getransformeerde data
de Kruskal-Wallis toets
geen enkele toets is mogelijk met deze data
De varianties zijn homogeen maar de residuen zijn niet normaal verdeeld. Een ANOVA zou
dus niet mogen (alternatief A).
De data logarithmisch transformeren maakt het probleem alleen maar erger omdat de
residuen links scheef verdeeld zijn. Door het transformeren wordt de verdeling nog meer
scheef naar links. Alternatief B is dus fout.
Alternatief D is een onzin antwoord want je had niet alleen de Kruskal-Waliis toets kunnen
gebruiken maar ook je had ook de anti-log kunnen nemen van de data in de hoop dat je dan
wel aan voorwaarden van de ANOVA gaat voldoen.