Bewegen met constante snelheid

WERKBLAD 5 - THEMA 14
(NIVEAU BETA)
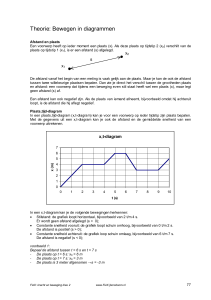
Bewegen met constante snelheid
Een voorwerp heeft een constante snelheid als het in gelijke tijdsduren (bijvoorbeeld elke seconde) steeds
dezelfde afstand aflegt. Het voorwerp voert een eenparige beweging uit.
Op de plaatjes hiernaast zie je hoe een brommer zich verplaatst in de tijd. Je ziet dat er in
gelijke tijdsduur gelijke afstanden worden afgelegd. De brommer rijdt dus steeds even hard.
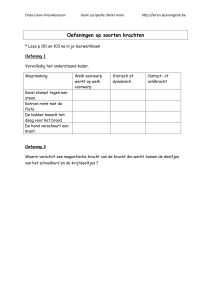
Je kunt een diagram maken van een beweging. Hierbij ga je afstand en tijd met elkaar
vergelijken. Hiervoor moet je weten dat er tussen elk plaatje 0,42 seconden.
De gegevens worden eerst in een tabel gezet, zie hieronder, en vervolgens in een diagram.
Zo’n diagram noem je een (afstand, tijd)-diagram.
Plaatje
1
2
3
4
5
Tijd (s)
0
0,42
0,84
1,26
1,48
Afstand (m)
0
0,3
0,6
0,9
1,2
Als het (afstand, tijd)-diagram van een beweging een schuine, rechte lijn te zien geeft, heeft het voorwerp
een constante snelheid.
Bij een constante snelheid is het verband tussen afstand en tijd recht evenredig en geldt de volgde
formule:
𝑎𝑓𝑠𝑡𝑎𝑛𝑑
𝑠
= 𝑠𝑛𝑒𝑙ℎ𝑒𝑖𝑑 𝑜𝑓
=𝑣
𝑡𝑖𝑗𝑑
𝑡
De gebruikte afkortingen komen uit het latijn. Het symbool voor snelheid is de kleine letter v (van het
Latijnse 'velocitas'). Het symbool voor afstand is s (van 'strada'). Voor de tijd gebruiken we de t (van
'tempo').
Rekenen met snelheden.
Bij het rekenen met snelheden, kun je gebruik maken van een formule, maar ook van een
verhoudingstabel. Hieronder volgen van beide voorbeelden. (Als je moeite hebt met formules bekijk dan
één van de formules op de site)
1
Bij het rekenen met snelheden kun je werken met 2 eenheden, de snelheid in m/s, of in km/h.
Welke tijdsduur je moet kiezen, hangt af van de situatie. In het verkeer wordt meestal met snelheden in
km/h gerekend.
Werken met verhoudingstabellen
Als voorbeeld rekenen we de constante snelheid van de brommer op de film uit. Er was gegeven dat in
1/24 s de brommer 0,3 m aflegt.
Stel nu de verhoudingstabel op, schrijf ook de grootheden daarin, in dit geval tijdsduur en afstand, vul in wat je weet en reken uit.
Afstand of s
Tijd of t
0,3 m
1/24 s
7,2m
1s
x 24
De snelheid is dus 7,2 m/s.
Je kunt deze snelheid nu omrekenen naar km/h. Bijvoorbeeld om te kijken of de brommer niet te hard
rijdt. Het omrekenen van m/s naar km/h, of omgekeerd, doe je altijd in een verhoudingstabel. Hierbij
gebruik je dan het gegeven dat er in 1 uur, 3600 s gaan.
Je krijgt de volgende tabel:
Afstand of s
Tijd of t
7,2
1s
25920 m = 26 km (afgerond)
3600 s = 1 uur
x 3600
De snelheid van de brommer is dus 26 km/h.
Met een verhoudingstabel ziet deze berekening er zo uit:
Werken met de formule
Een voorbeeld: Je loopt met constante snelheid een afstand van 42 m. Je doet daar 12 s over. Jouw
snelheid over die afstand is: v = afstand/tijdsduur = s/t = 42/12 = 3,5 m/s
Na het stuk gemiddelde snelheid staan meer voorbeelden hoe je kunt rekenen.
De gemiddelde snelheid
Vaak bewegen voertuigen niet met een constante snelheid. Daarom heeft men in de natuurkunde een
andere begrip bedacht, de gemiddelde snelheid. Met de gemiddelde snelheid wordt aangegeven met
welke constante snelheid een voertuig gereden zou moeten hebben om een bepaalde afstand, in een
bepaalde tijd af te leggen.
Stel dat je op bezoek gaat bij een familielid en dat de afstand die je moet afleggen voordat je bij dat
familielid bent aangekomen 80 km is. Als je nu 1 uur er over doet om daar te komen is je gemiddelde
snelheid 80 km/h geweest. Dat betekent niet dat je ook de hele tijd gereisd hebt met die snelheid. Je zult
misschien harder hebben gereden op de snelweg, maar soms ook stil hebben gestaan voor een stoplicht.
Bij het rekenen met de gemiddelde snelheid wordt de formule een klein beetje aangepast:
𝑎𝑓𝑠𝑡𝑎𝑛𝑑
𝑠
= 𝑔𝑒𝑚𝑖𝑑𝑑𝑒𝑙𝑑𝑒 𝑠𝑛𝑒𝑙ℎ𝑒𝑖𝑑 𝑜𝑓
=< 𝑣 >
𝑡𝑖𝑗𝑑
𝑡
Vragen
2
Maak je berekeningen op papier, (je moet de berekening steeds volledig opschrijven) en maak een foto
die je in het document voegt.
1.
Reken de volgende snelheden om in km/h:
a. 35 m/s;
b. 5,2 m/s;
2. je fietst een stuk met een constante snelheid van 22 km/h. Bereken de afstand die je aflegt:
a. in 10 minuten;
b. Hoe lang zou je die snelheid moeten volhouden om een afstand van 6,0 km af te leggen?
3.
De snelheid van het geluid bedraagt 1150 km/h.
a. Reken deze snelheid om in m/s; rond af op een geheel getal.
In Duitsland is een gat geboord van 18 km diep.
b. Bereken de tijd die het geluid van jouw stem nodig heeft om de bodem
te bereiken.
c. Hoe lang nadat het geluid is voortgebracht, zou je het weer horen?
d. Vergelijk je antwoord met de cartoon.
4. Robin kan goed hardlopen. In 2,2 uur tijd loopt hij een afstand van 19 km.
a. Bereken zijn gemiddelde snelheid.
b. Waarom moet je dit een gemiddelde snelheid noemen?
Bewegen met niet constante snelheid
Bijna nooit rijdt een voertuig met een constante snelheid. Dat betekent dat het voertuig op dat moment
of sneller gaat voortbewegen, hij versnelt dan, of dat hij langzamer gaat voortbewegen, hij vertraagt dan.
Een bijzonder situatie ontstaat als een voorwerp in beweging komt waarbij dit voorwerp zelf een
constante kracht uitoefent. Omdat de snelheid in het begin laag is, zijn de tegenwerkende krachten klein
en kan het voertuig versnellen. Maar hierdoor wordt de tegenwerking groter en zal op een gegeven
moment de tegenwerking zo groot worden dat de snelheid constant wordt.
Vragen
5. Als een auto beging met rijden werkt er op dat moment één kracht die constant is en die de auto
versnelt.
a. Hoe noemen we de beweging die de auto uitvoert zolang alleen deze ene kracht op de auto
werkt?
6.
Op de auto werkt echter ook een wrijvingskracht die groter wordt naarmate de auto sneller gaat
rijden. Hierdoor wordt de snelheid op een gegeven moment constant.
b. Leg uit wat er met de resulterende kracht op de auto gebeurd gedurende het versnellen.
Een blad valt van een boom en dwarrelt naar beneden.
a. Leg uit wat voor type beweging(en) het blad uitvoert.
Terwijl het blad omlaag gaat is tijdens dit dwarrelen de resulterende kracht op het blad soms
omhoog gericht.
b. Leg uit wat voor soort beweging het blad dan uitvoert.
Op de volgende bladzijden staan nog extra voorbeelden hoe te rekenen.
3
Voorbeelden
Hieronder staan nog een aantal voorbeelden hoe je kunt rekenen bij gebruik van het begrip snelheid.
Soms is van een bewegend voorwerp de snelheid bekend. In zo'n situatie kun je bijvoorbeeld de afstand
uitrekenen die het voorwerp in een bepaalde tijd aflegt.
Voorbeeld (1): Je rijdt met een auto op de snelweg een kwartier lang met een constante snelheid van 90
km/h. Hoe groot is de afstand die je dan aflegt?
De formule luidt: s/t = v, breng de t naar de ander kant, dan krijg je s = v x t
- de snelheid is 90 km/h en de tijdsduur is 1 kwartier, dus 0,25 uur.
Invullen in de formule geeft de gezochte afstand: s = v * t = 90 x 0,25 = 22, 5 km.
Wil je weten hoe lang een auto over een bepaalde afstand doet, kun je weer de formule omschrijven. Ga
uit van de formule s = v x t en breng nu de v naar de andere kant, je krijgt dan s/v = t oftewel t = s/v.
Toepassen in een voorbeeld geeft.
Voorbeeld (2): Je rijdt met een constante snelheid van 90 km/h. Hoe lang doe je over een
afstand van 60 km?
Gebruik de formule t = s/v = 60/90 = 2/3 uur oftewel 40 minuten.
Zowel voorbeeld(1), als voorbeeld (2) kun je oplossen met een verhoudingstabel
Voorbeeld (2)
Omdat de snelheid 90 km/h is kun je, als je bij de tijd 1 uur neemt, voor de afstand 90 km nemen. De
tijdsduur in de vraag is 15 minuten, gevraagd de afgelegde afstand.
Afstand of s
Tijd of t
90 km
1 uur
22,5 km
15 min = 0,25 uur
x4
Voorbeeld (3)
Omdat de snelheid 90 km/h is kun je, als je bij de tijd 1 uur neemt, voor de afstand 90 km nemen. De
afstand in de vraag is nu 60 km, gevraagd de tijd.
Afstand of s
Tijd of t
90 km
1 uur
60 km
2/3 uur = 40 minuten
:90 x 60
4